01. 概论
圆的面积
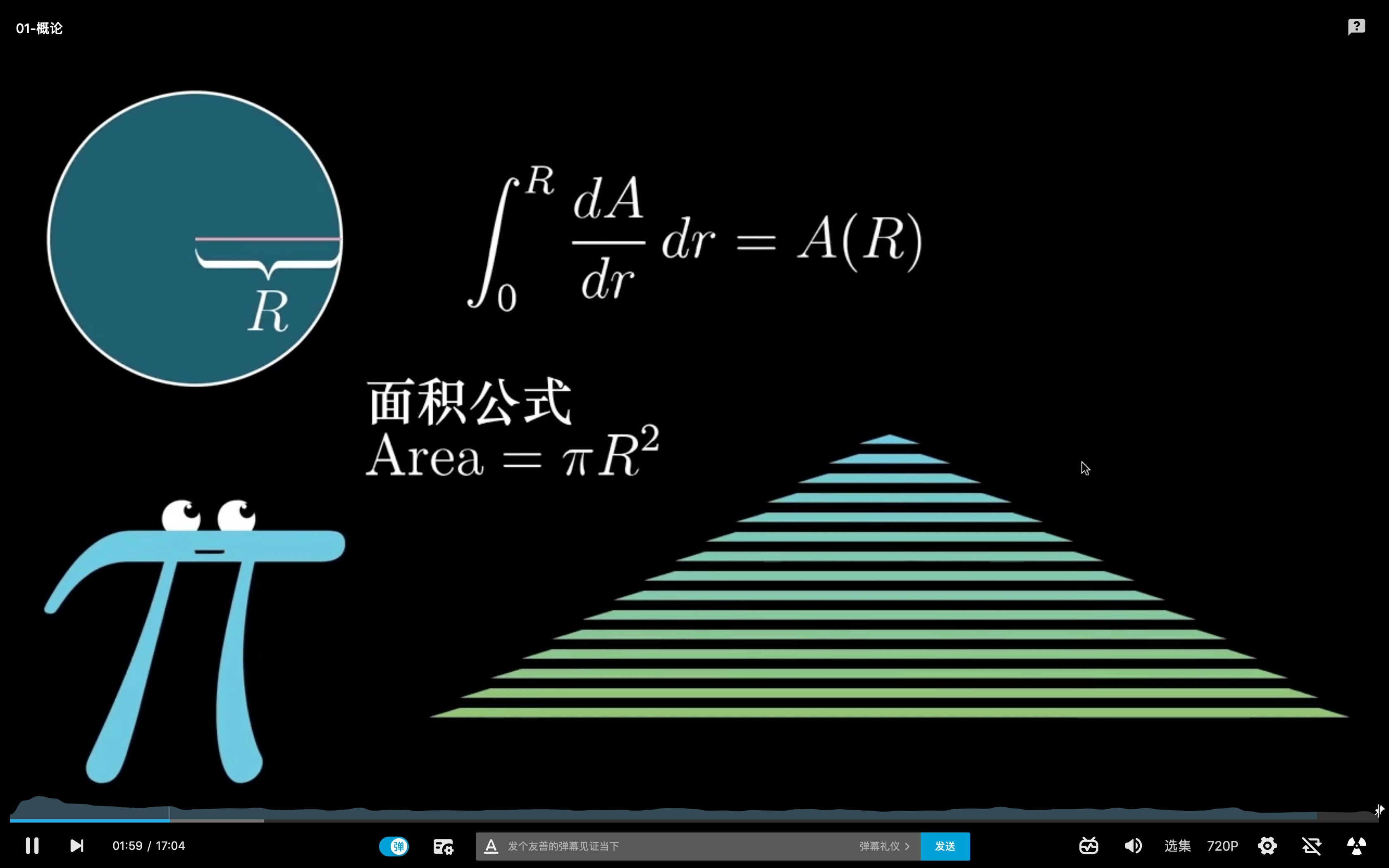
02. 导数的悖论
微积分之父

汽车
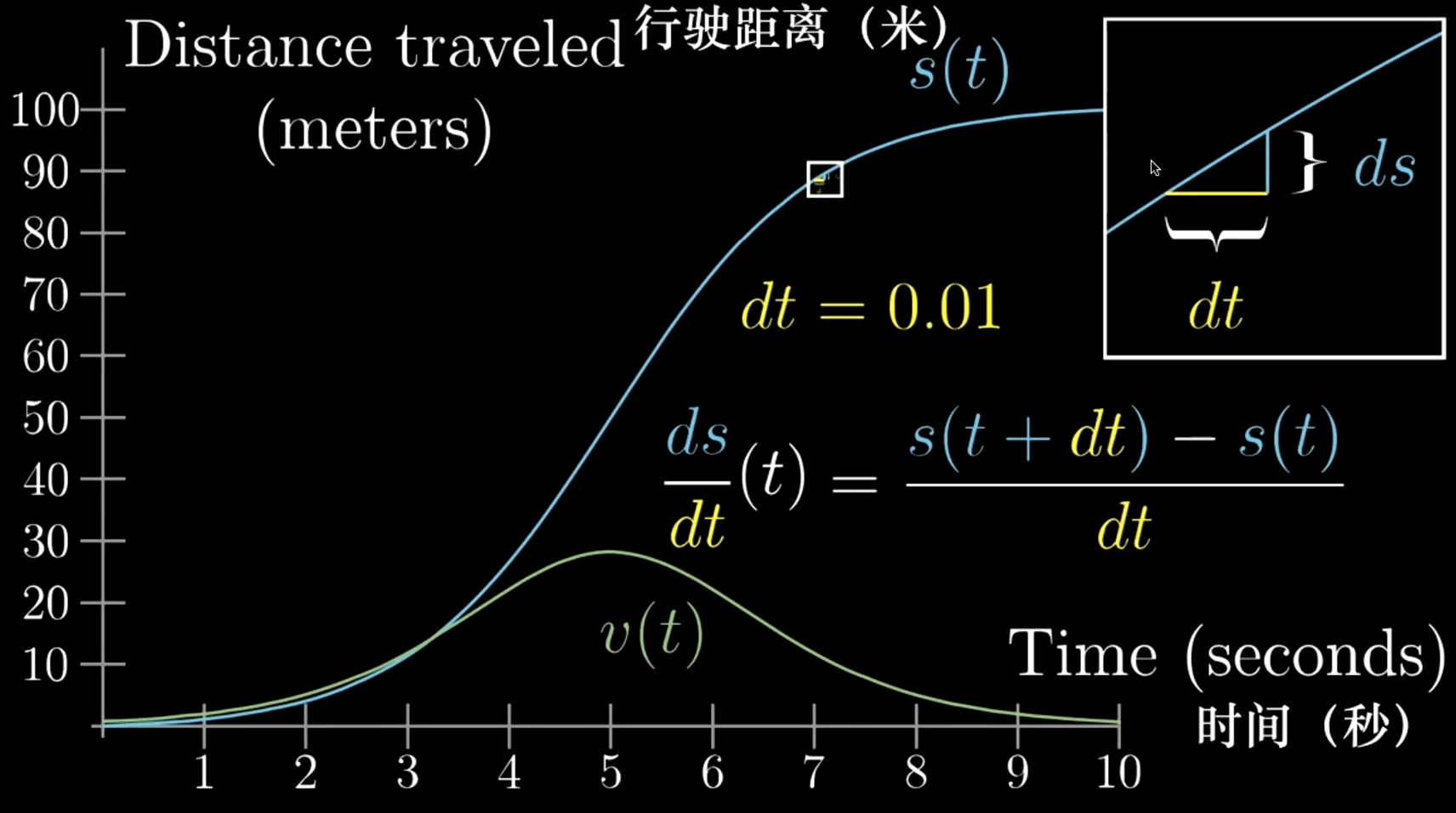
03. 用几何来求导
应用
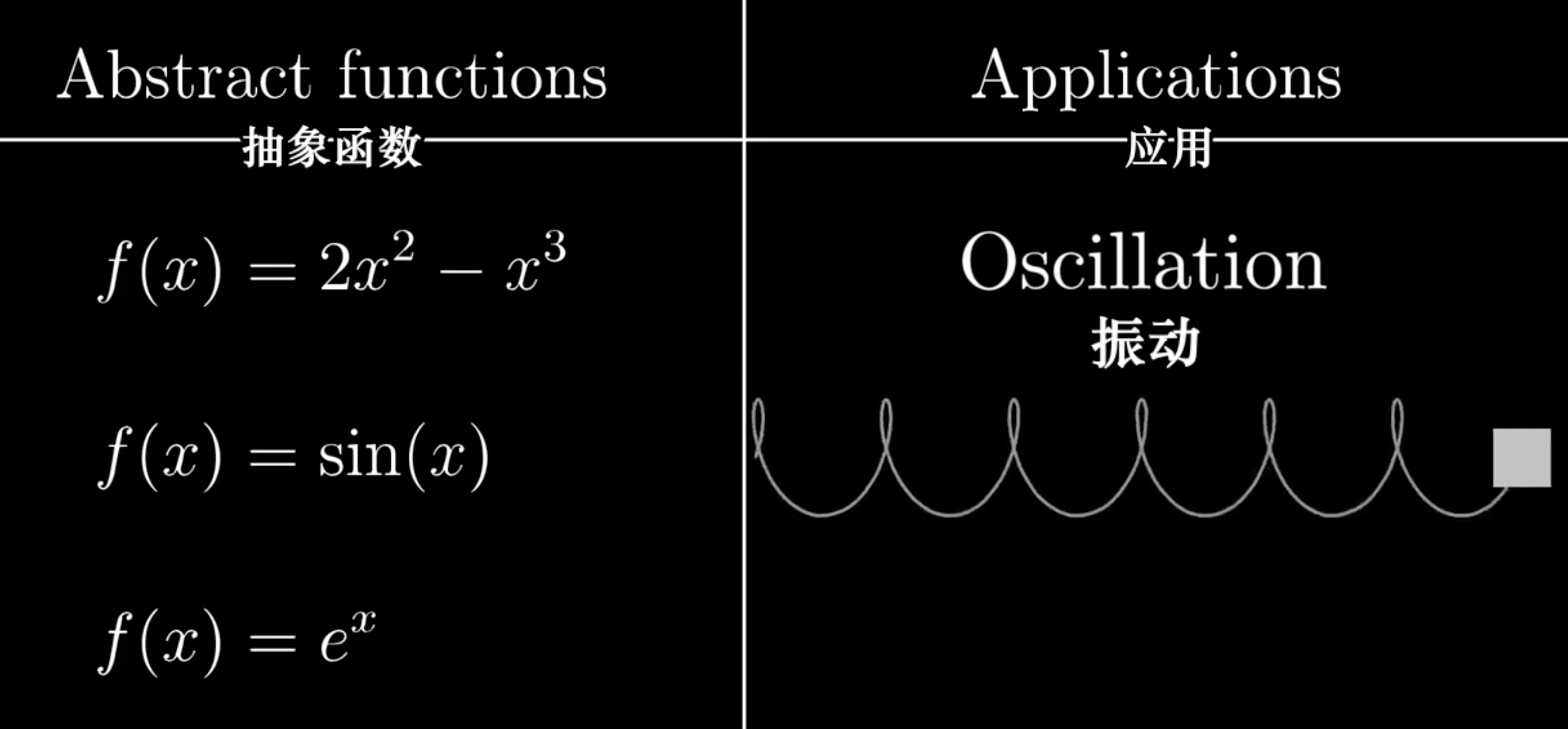
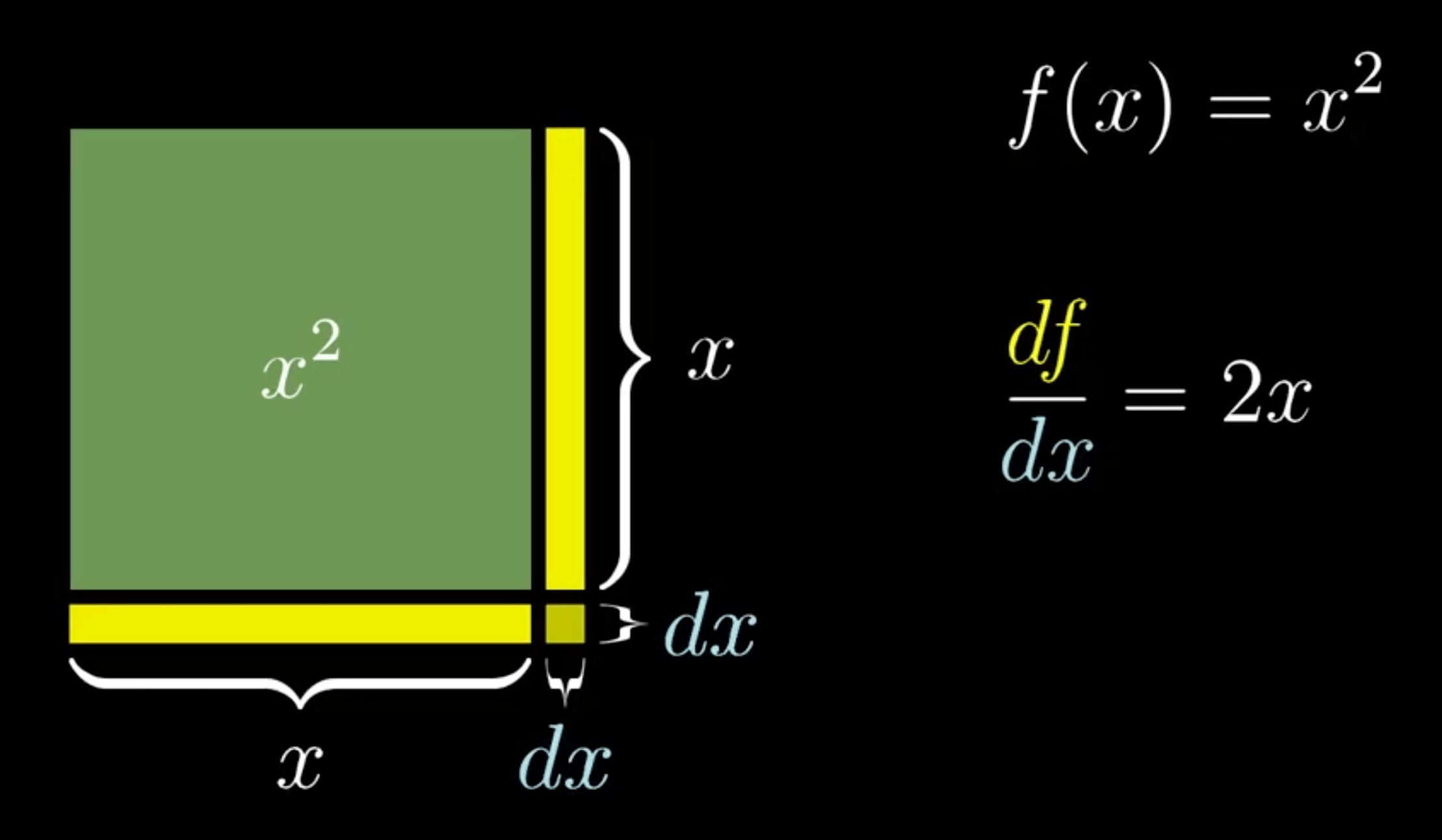
\(x^{2}\)
\(x^{3}\)

\(x^{n}\)

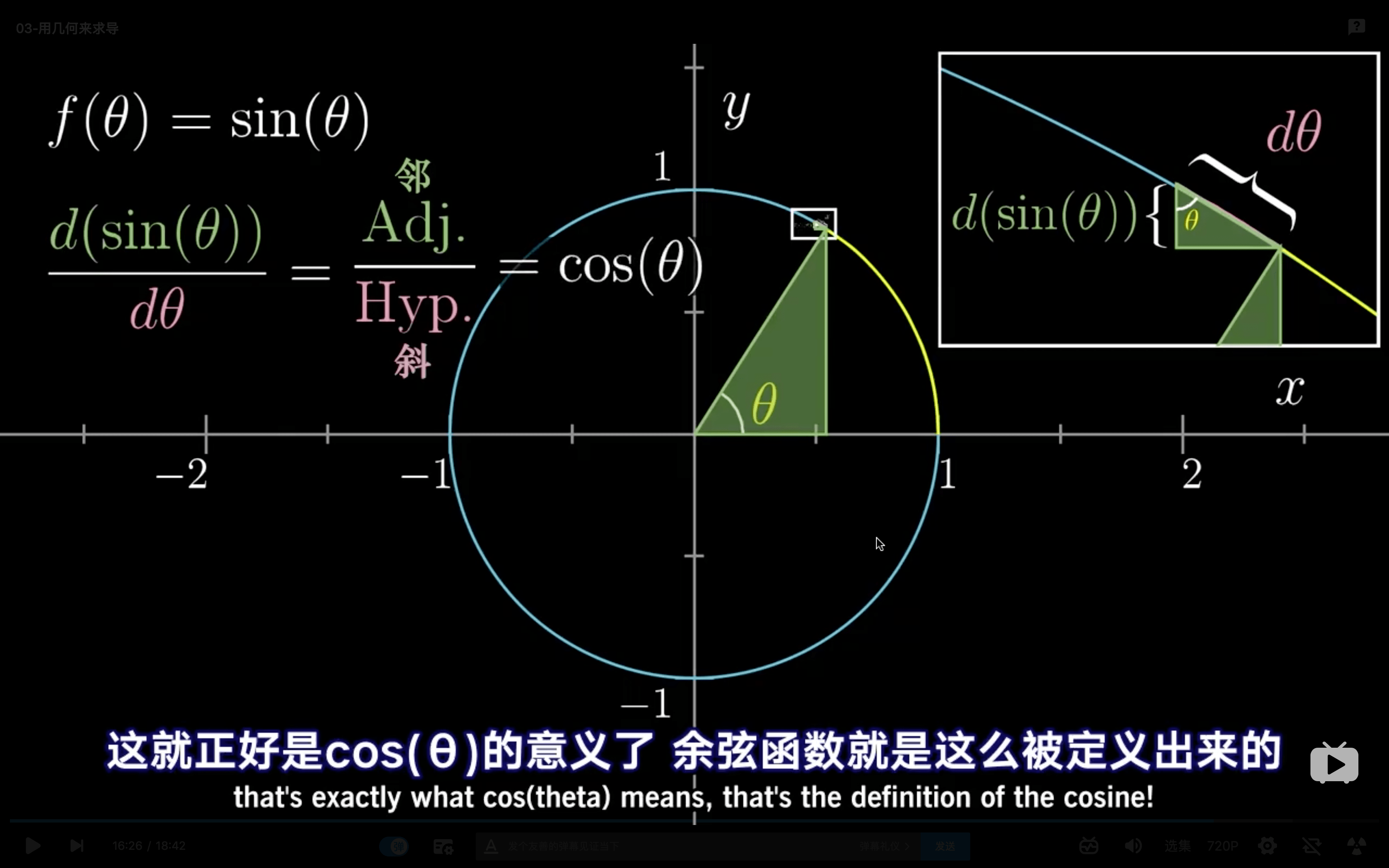
\(\sin(x)\)
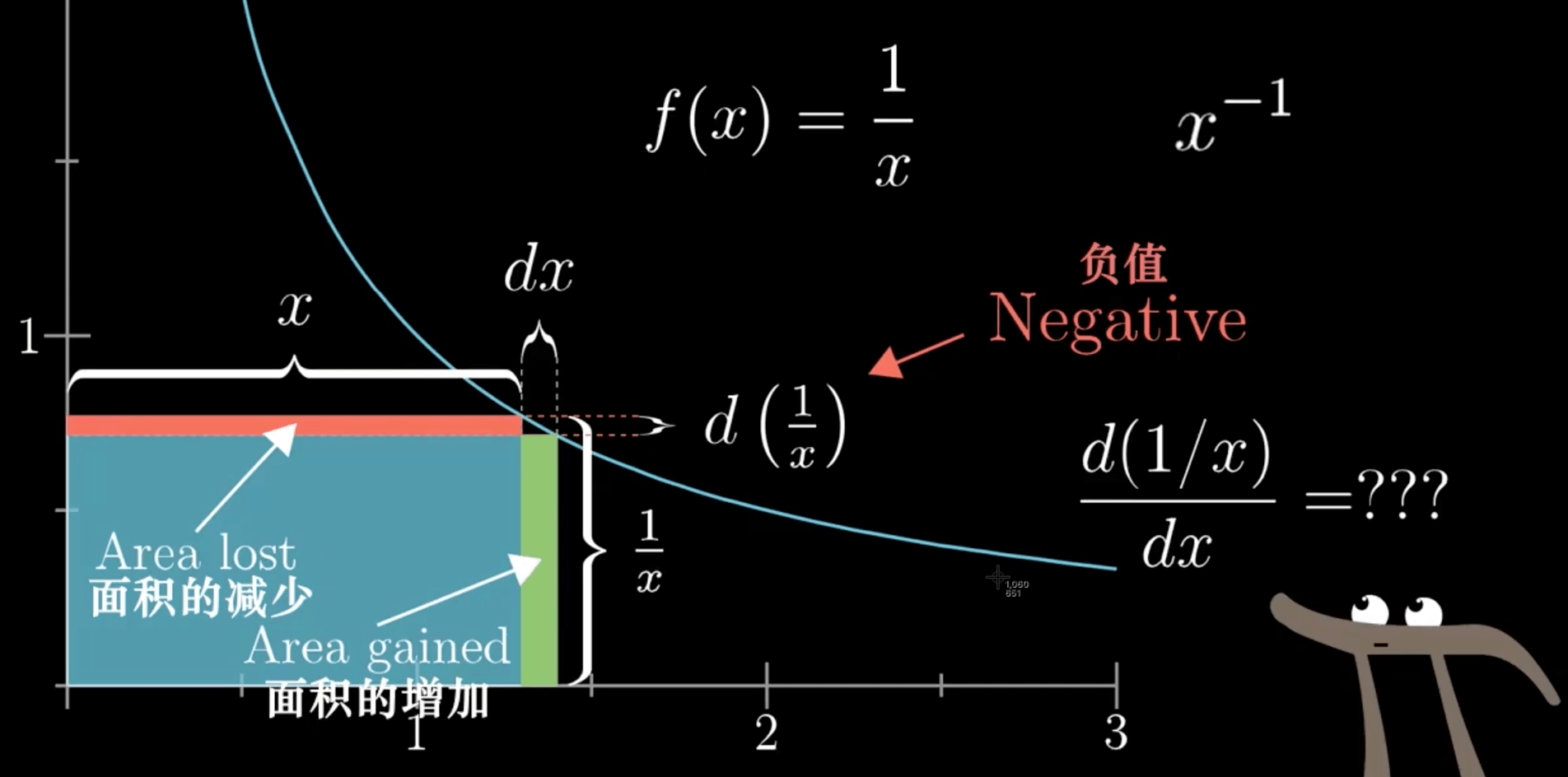
\(\frac{1}{x})\)
04. 直观理解链式法则和乘积法则
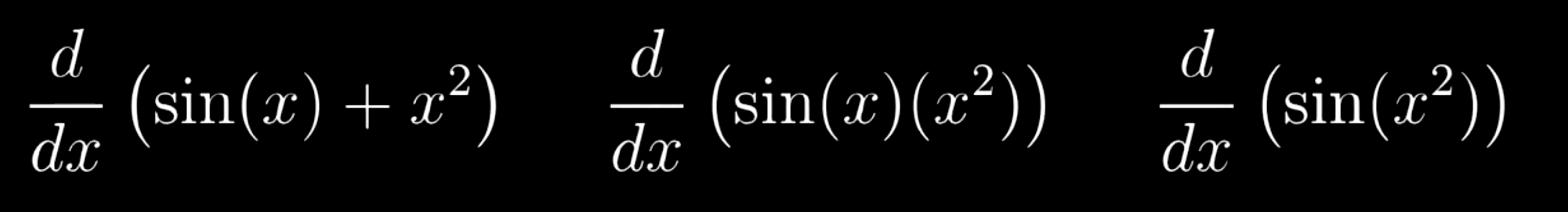
组合函数 求导
- 加 Sum
- 乘 Product
- 复合 Composition
加法法则
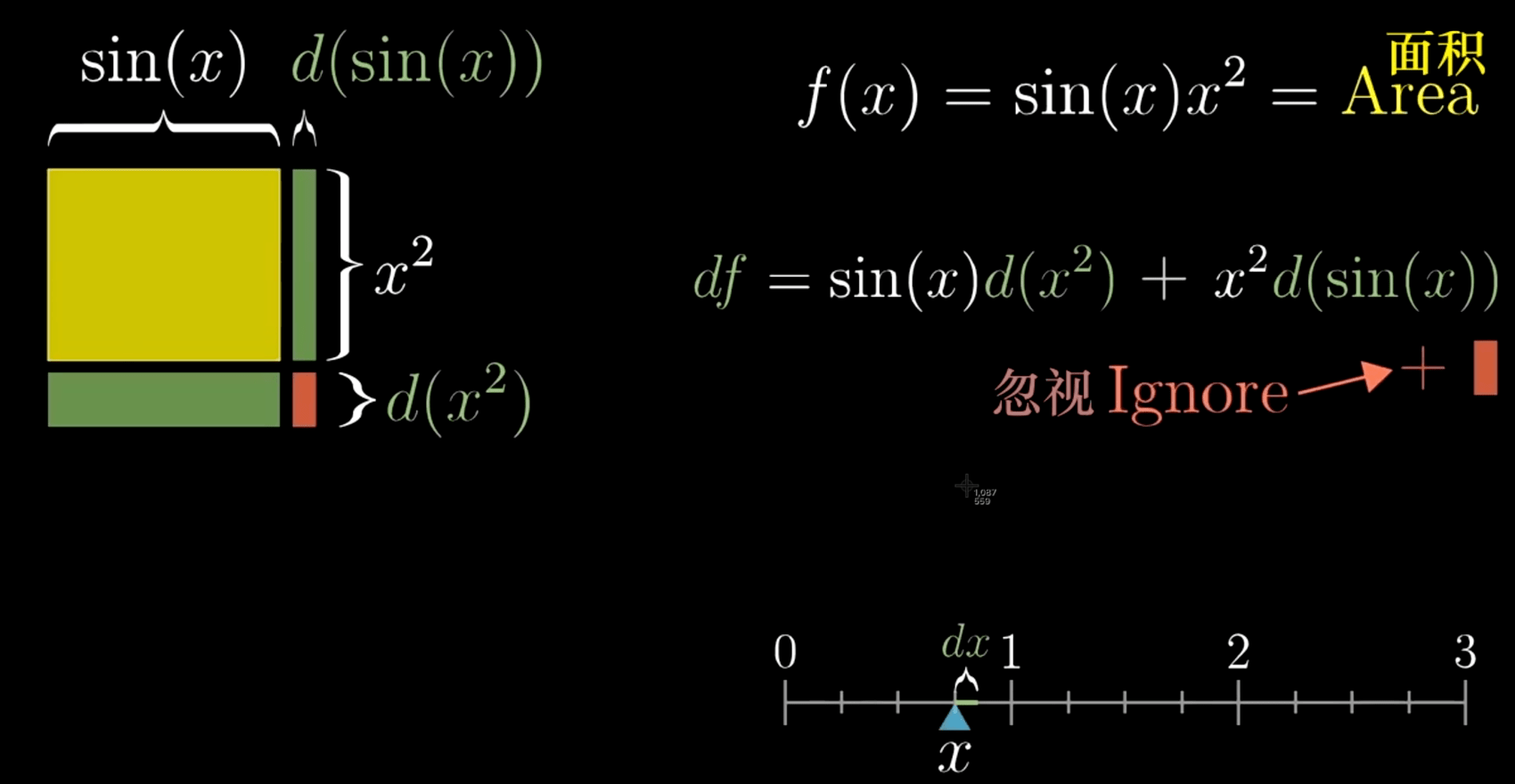

乘积法则
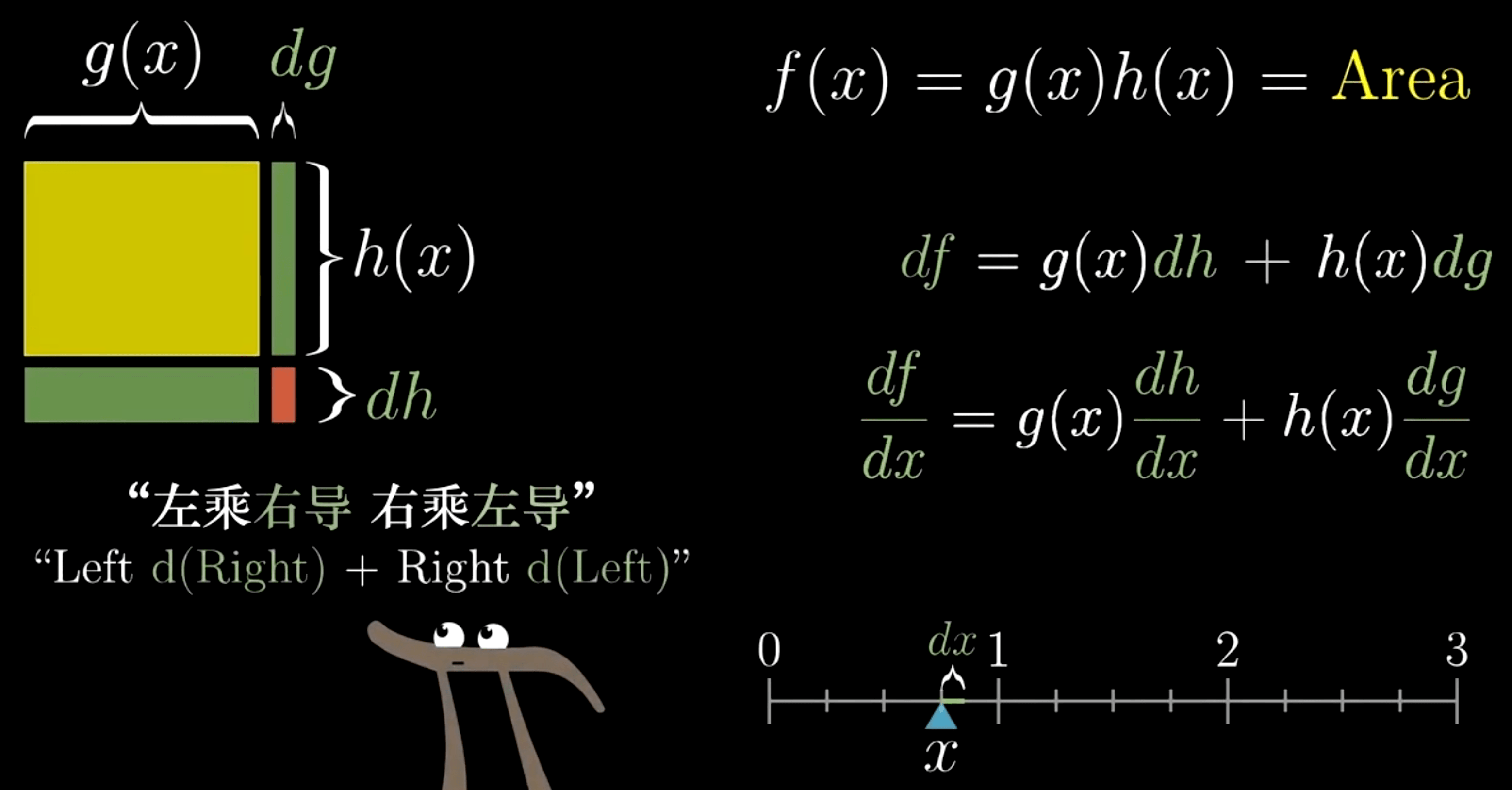
复合:链式法则

05. 指数函数求导
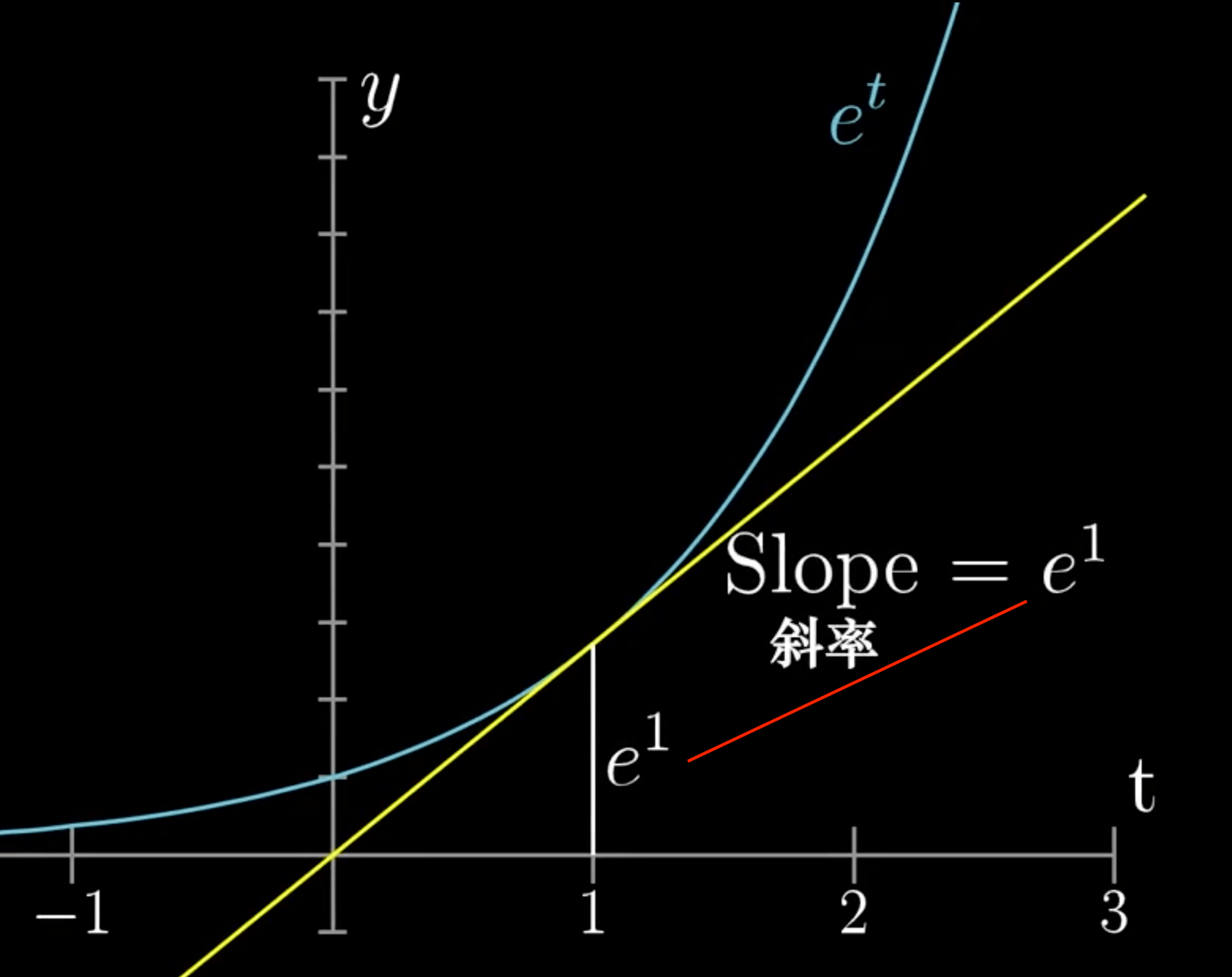
2的指数 -> e表示

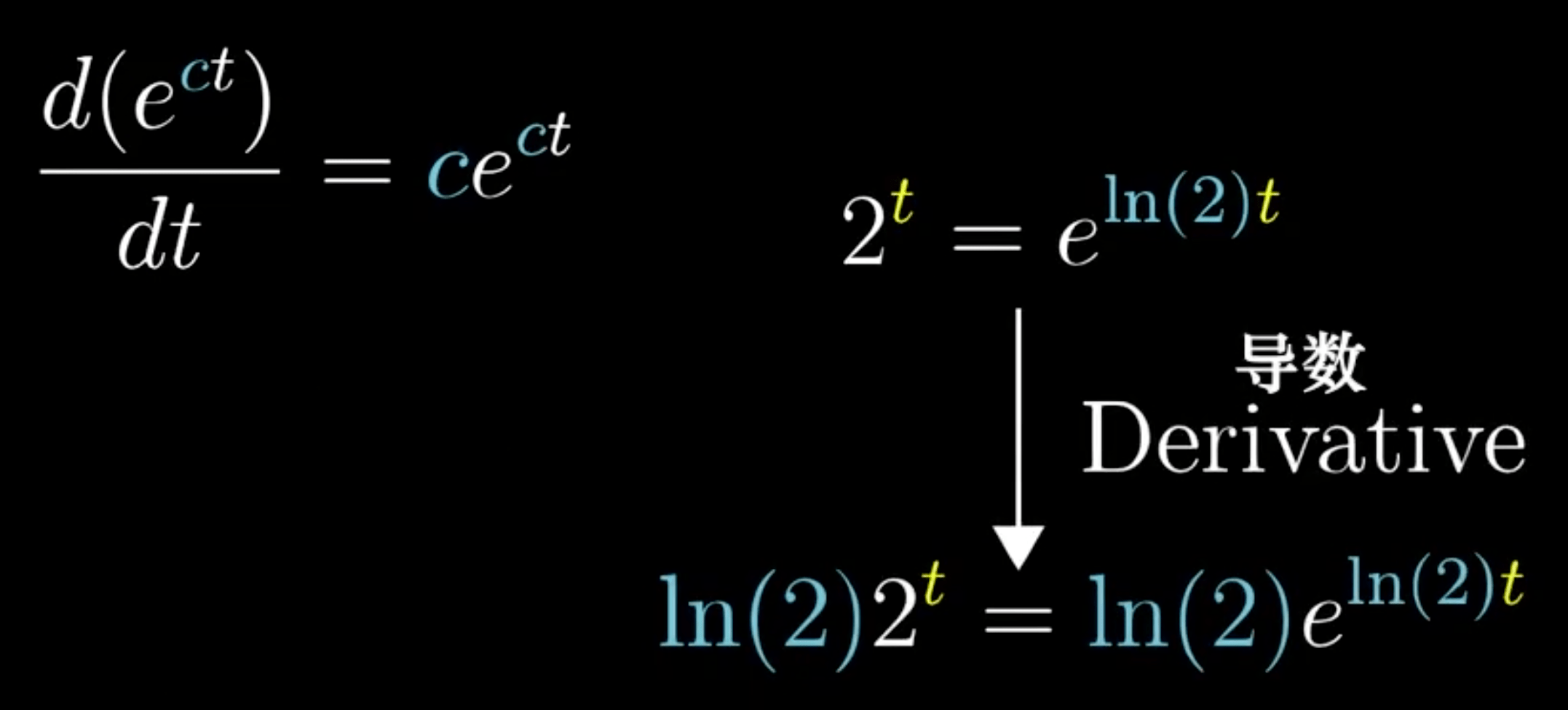
06. 隐函数求导是怎么回事
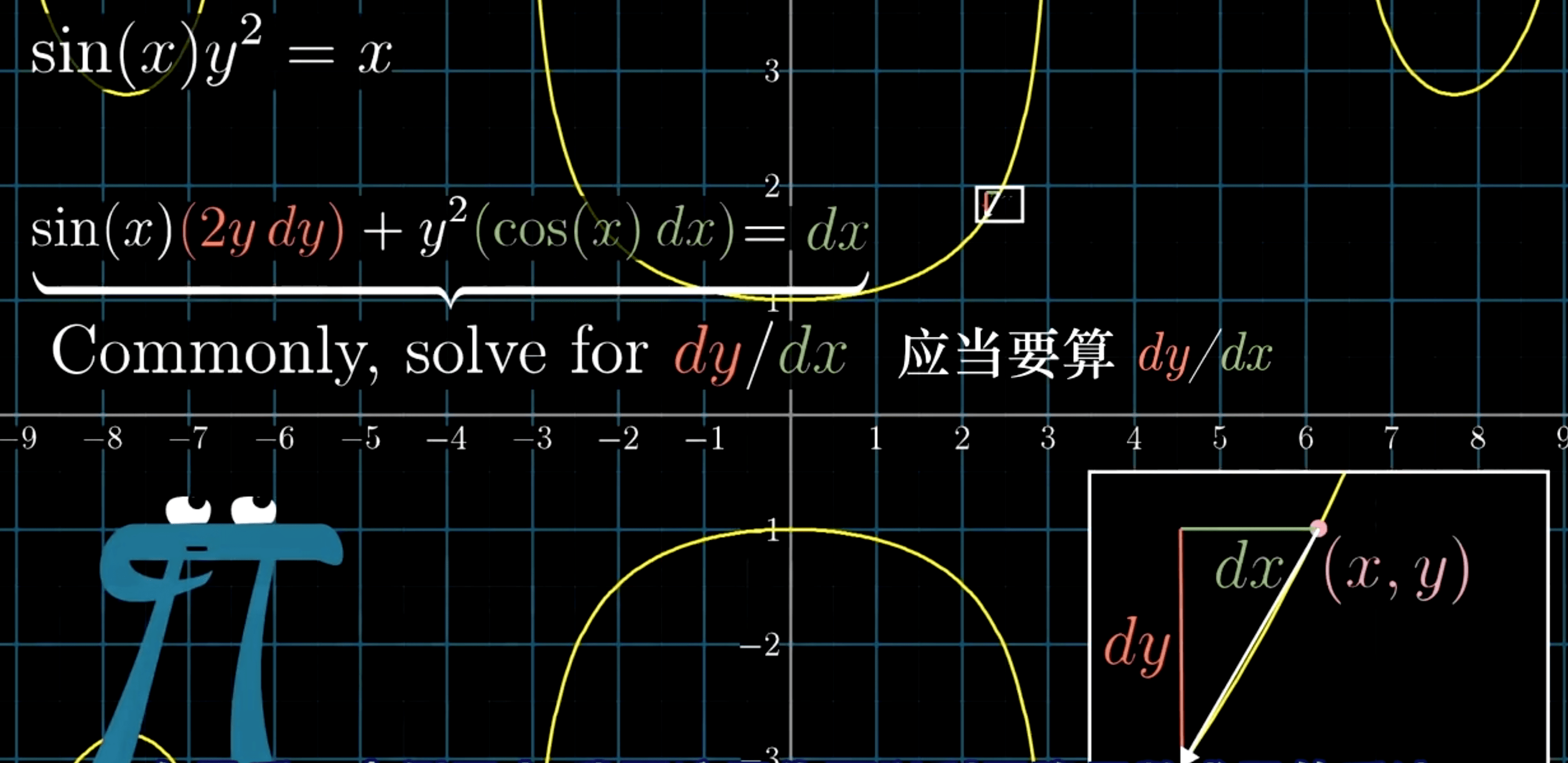
变化落在函数曲线上
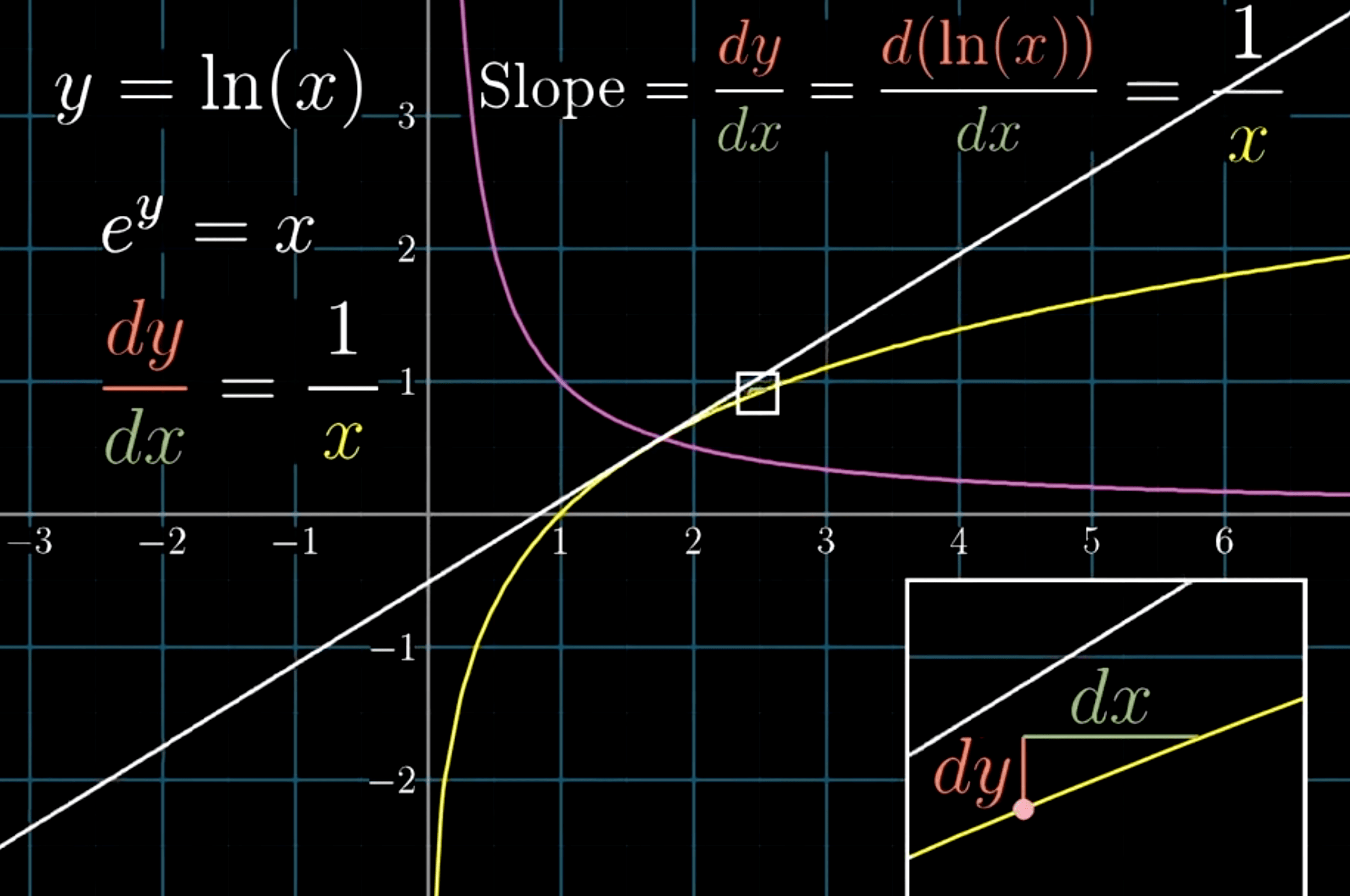
07. 极限
目标

导数定义
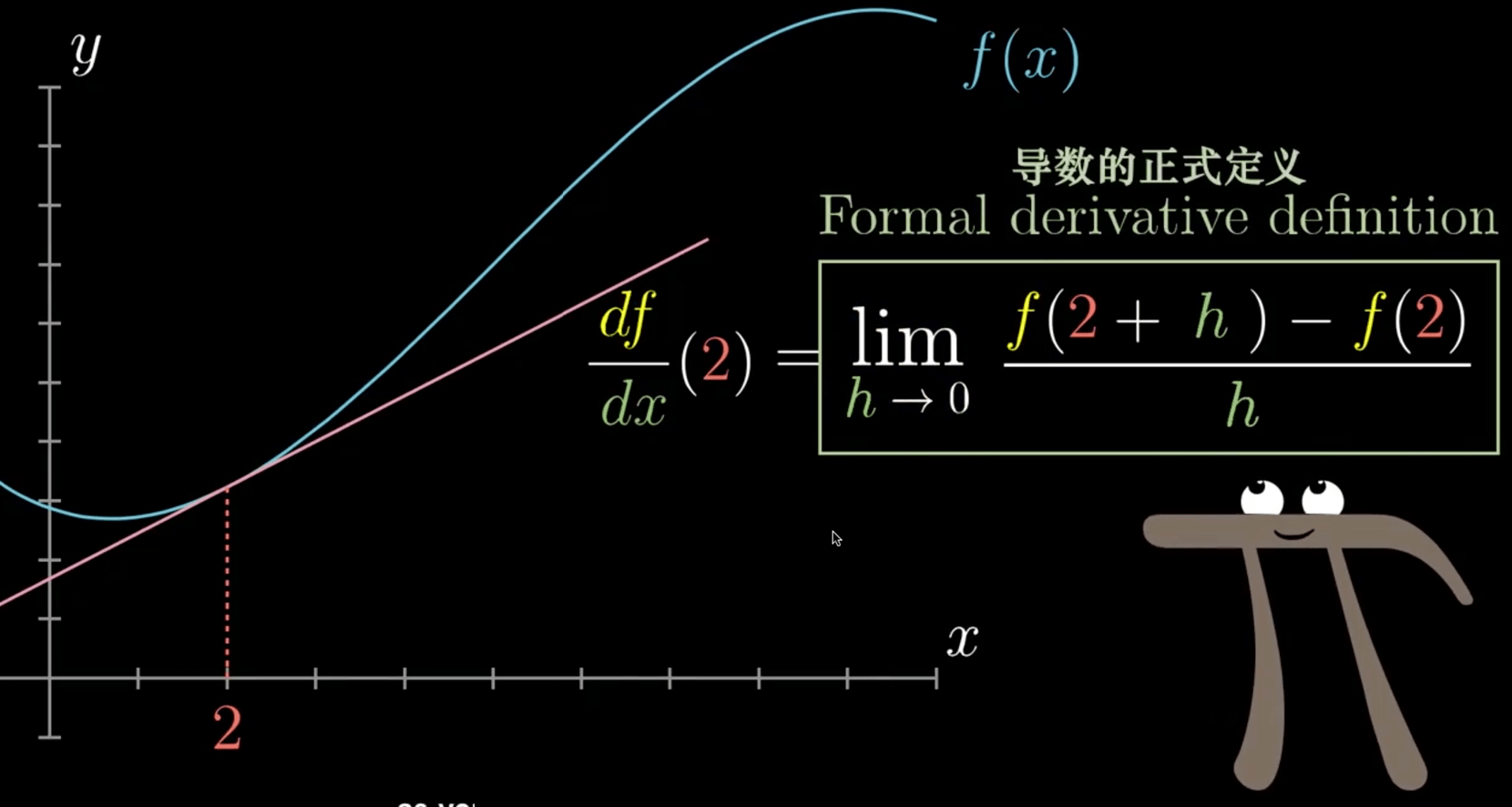
\(dx\) -> \(h\)
- 明确表示 \(h\) 是一个普通的数,与无穷小无关
- \(dx\) 就是无穷小量
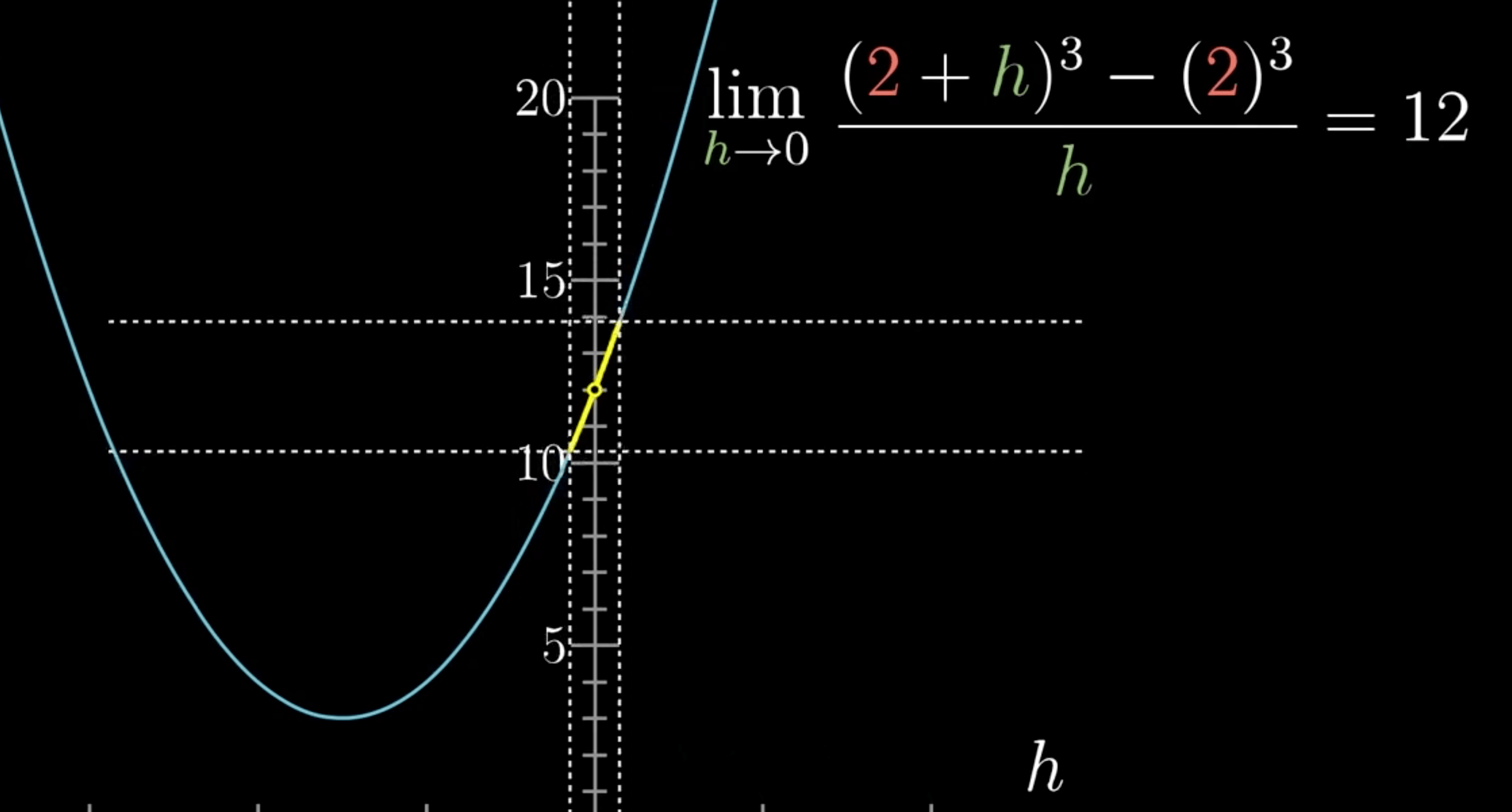
\(\frac{0}{0}\)
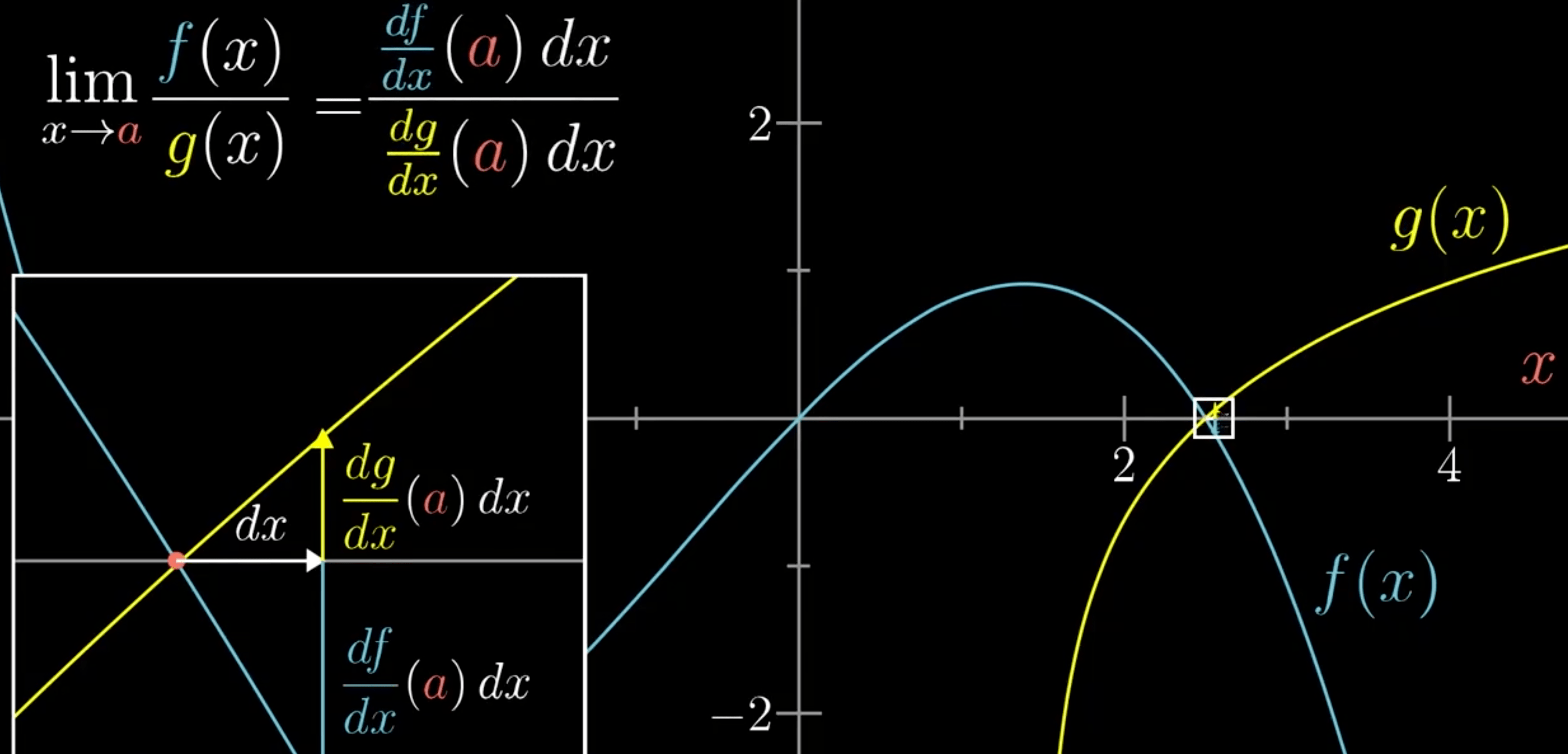
08. 积分与微积分的基本定理
积分
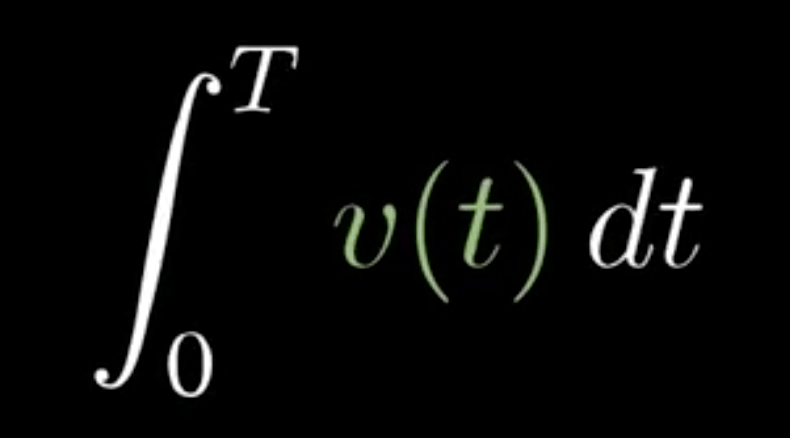
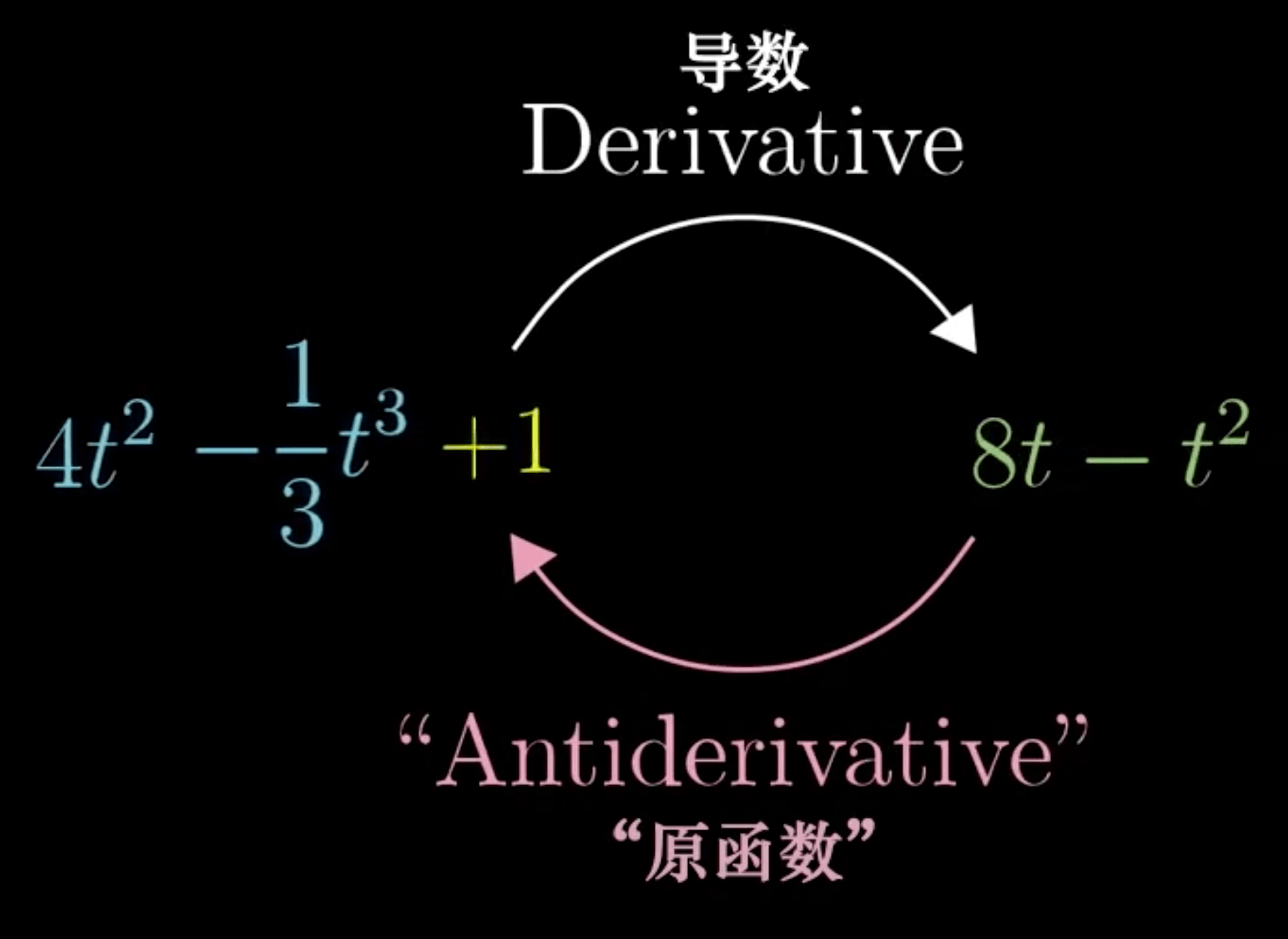
积分:求导的逆运算
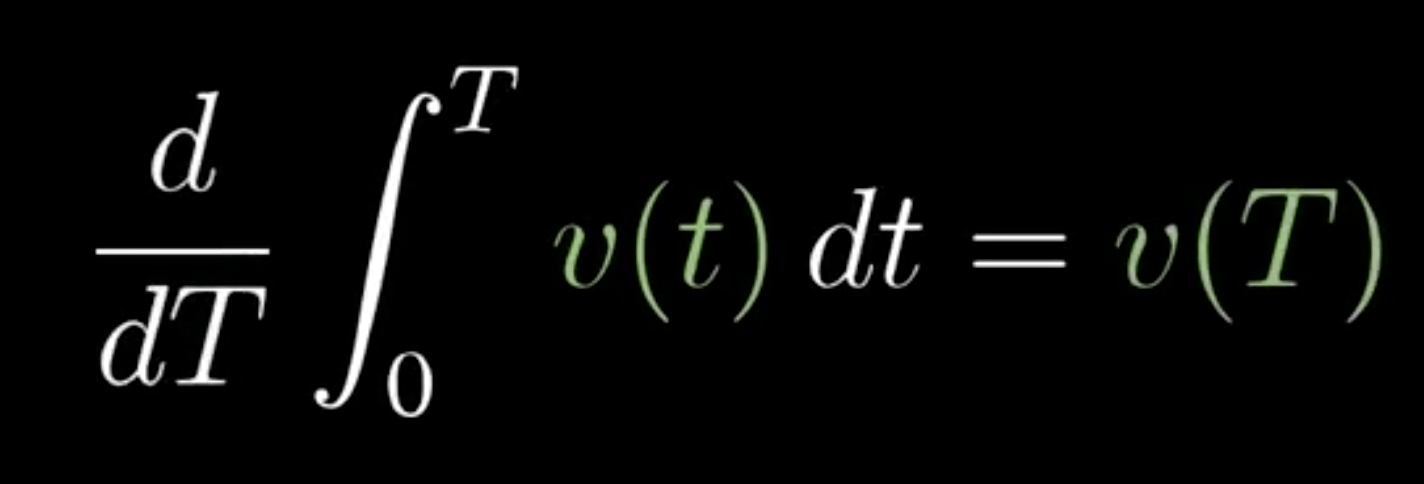
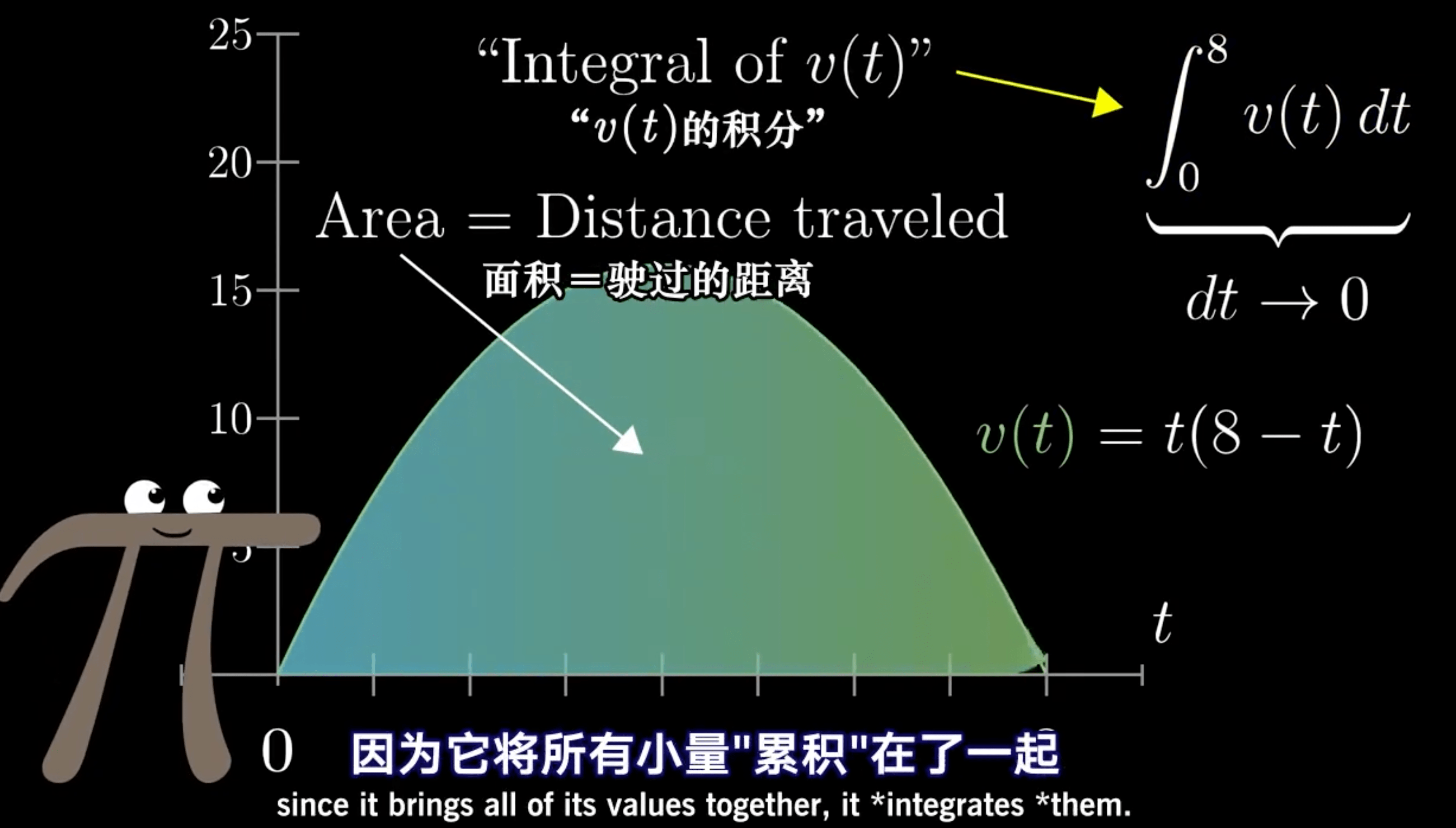
积分:小量累积
微积分基本定理
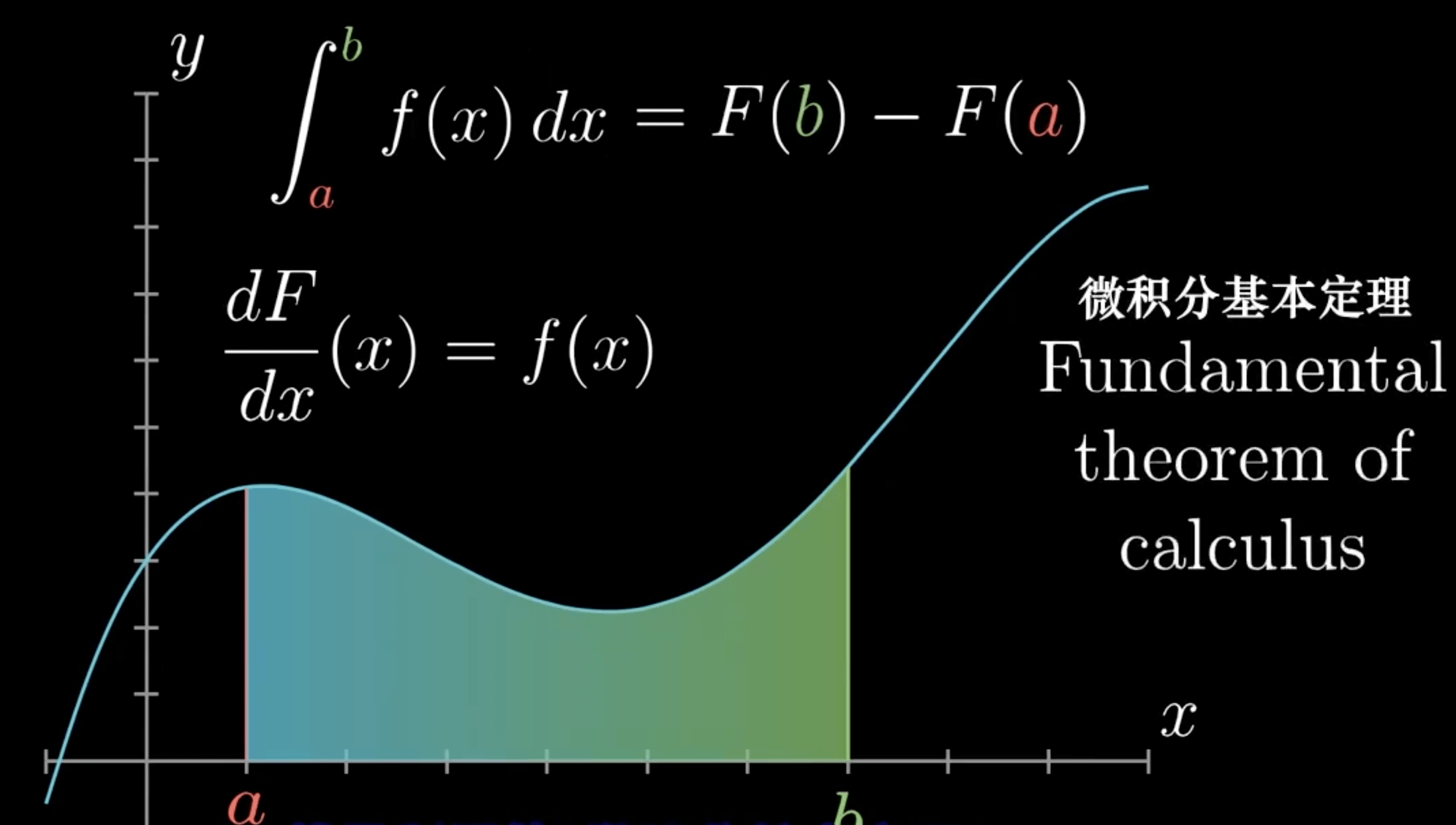
原函数 <==> 导数
09. 面积与斜率有什么关系
平均值
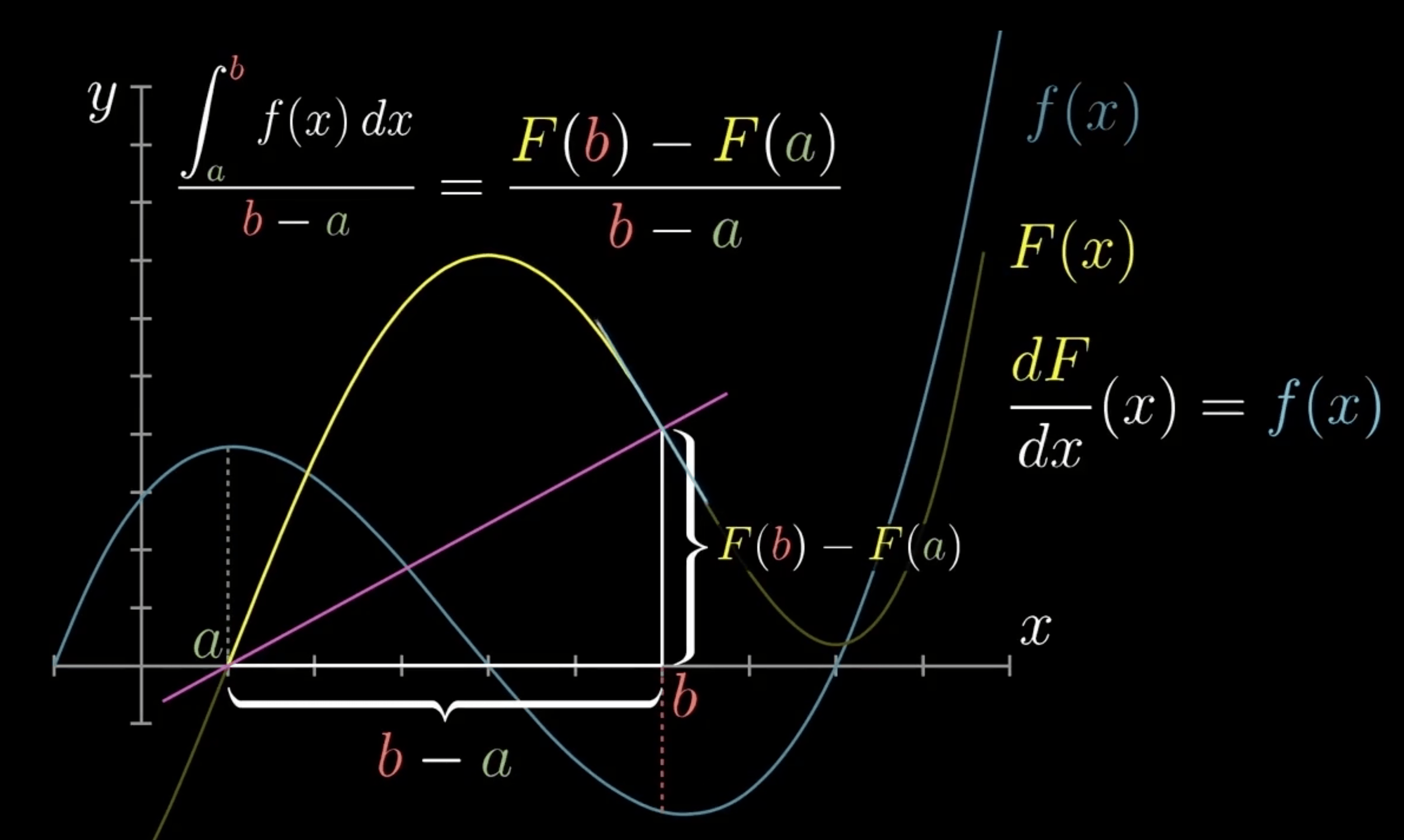
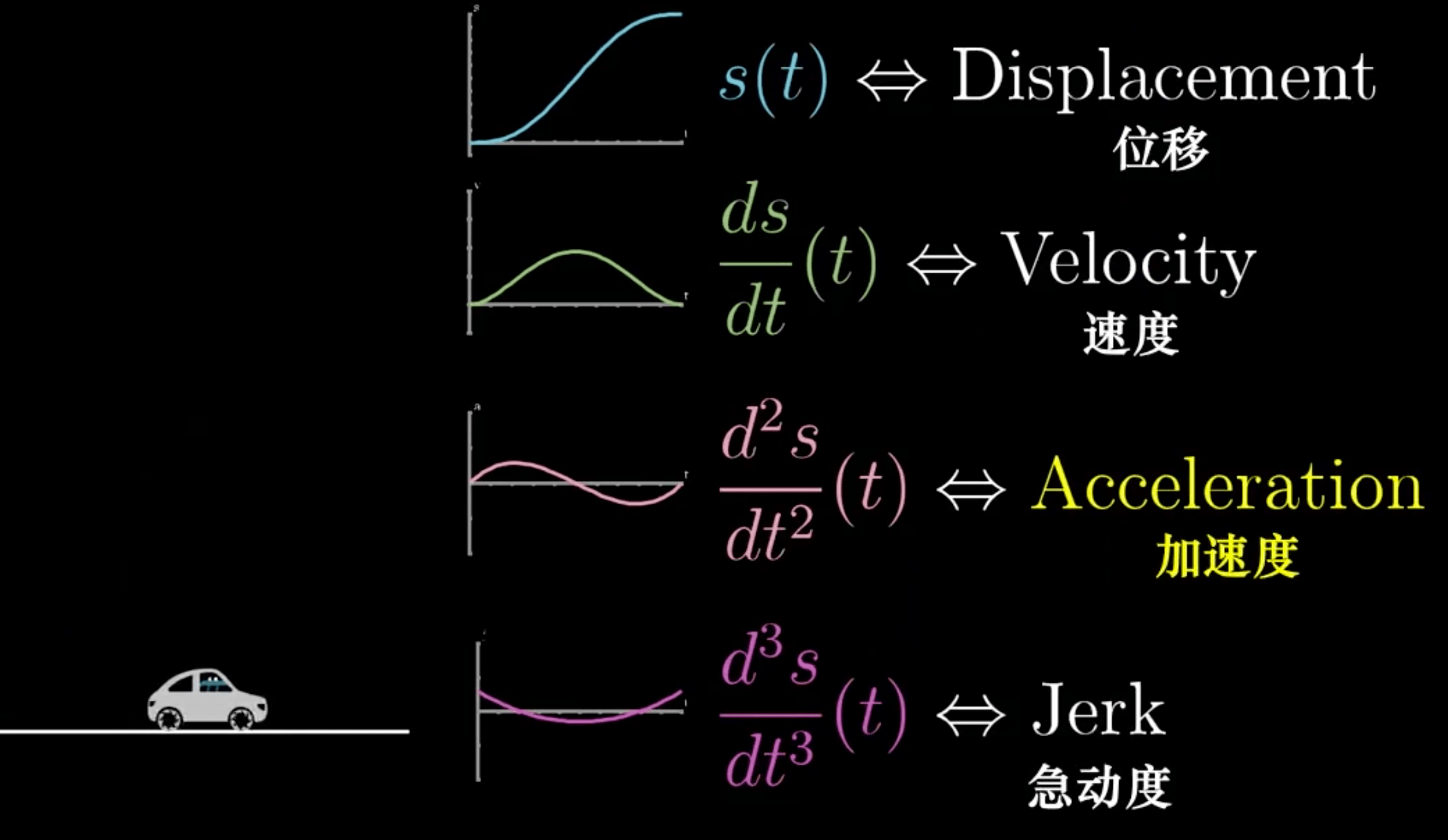
09脚注-高阶导数
二阶导数
- 导数的导数
- 变化量的变化量
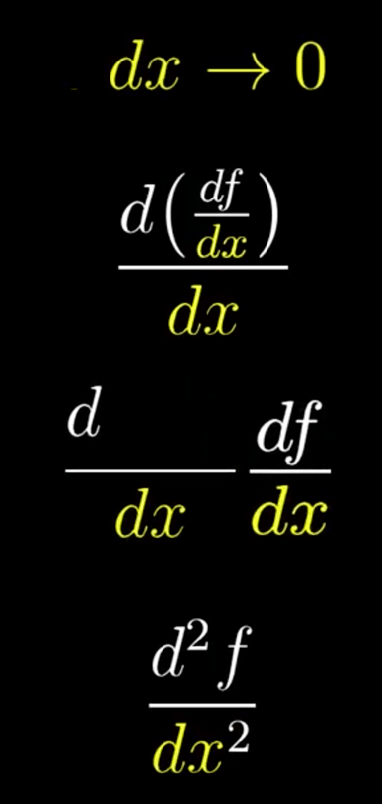
高阶导数
10. 泰勒级数
泰勒级数是利用函数某单个点的导数来近似这个点附近函数的值
用多项式 近似 其它函数
- 好计算
- 好求导
- 好积分
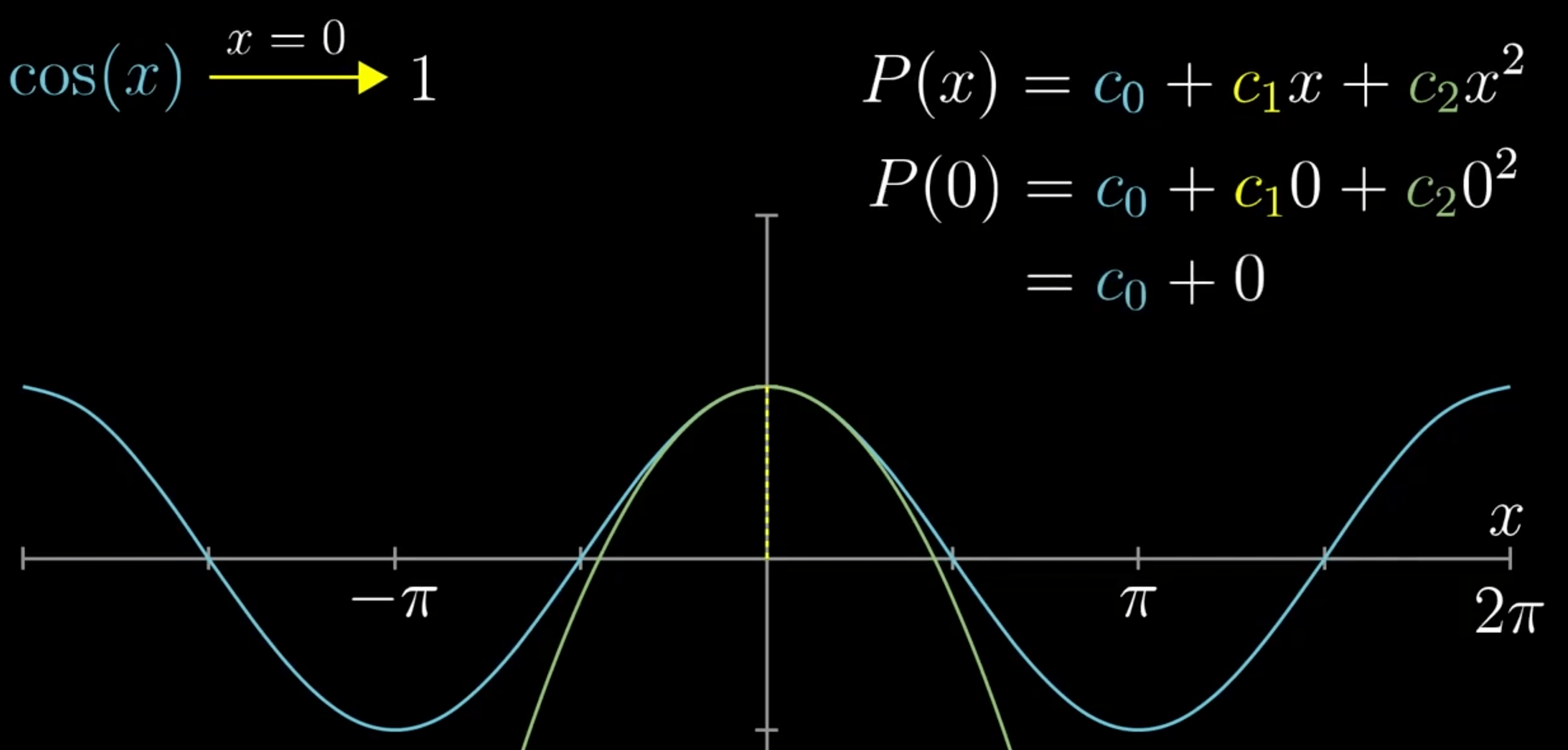
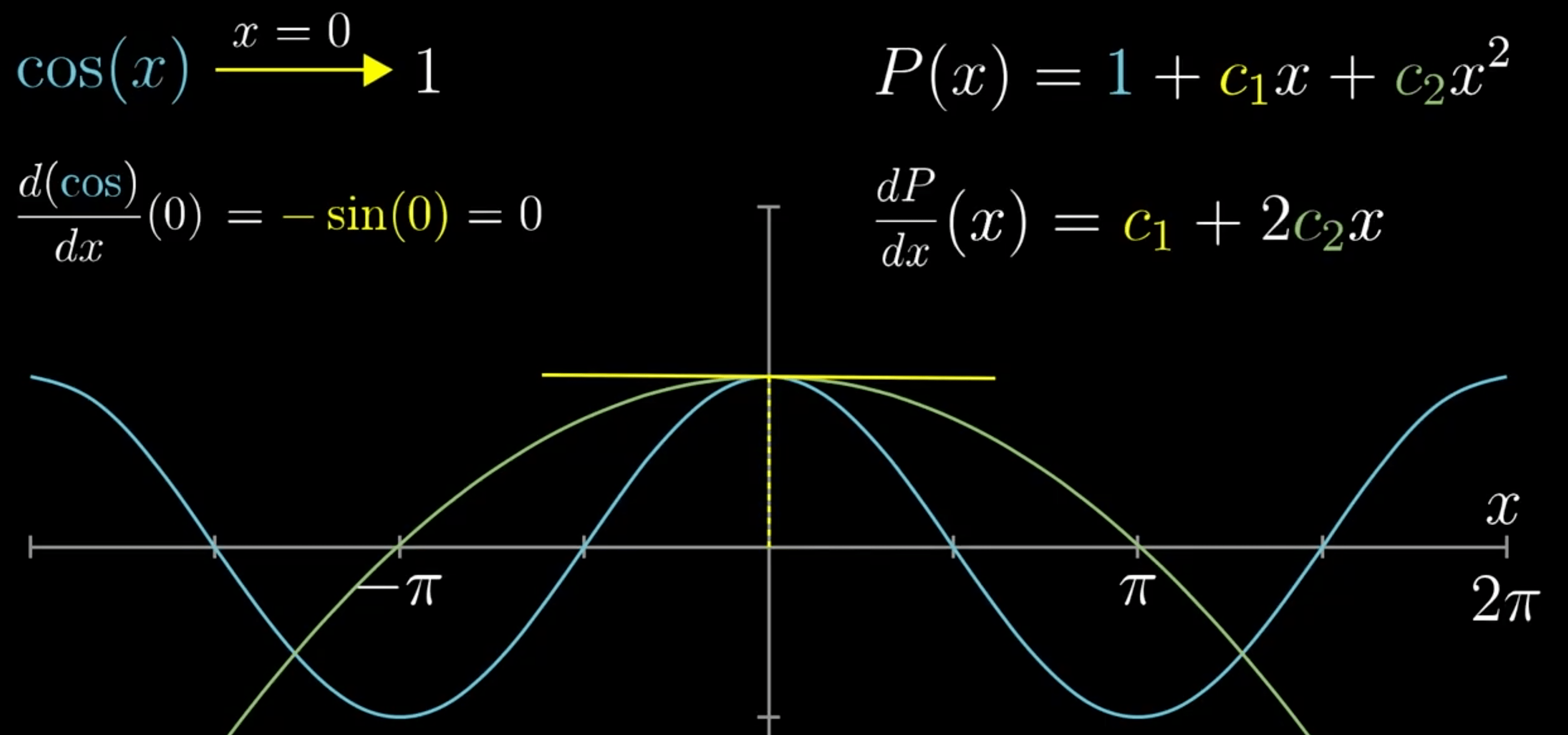
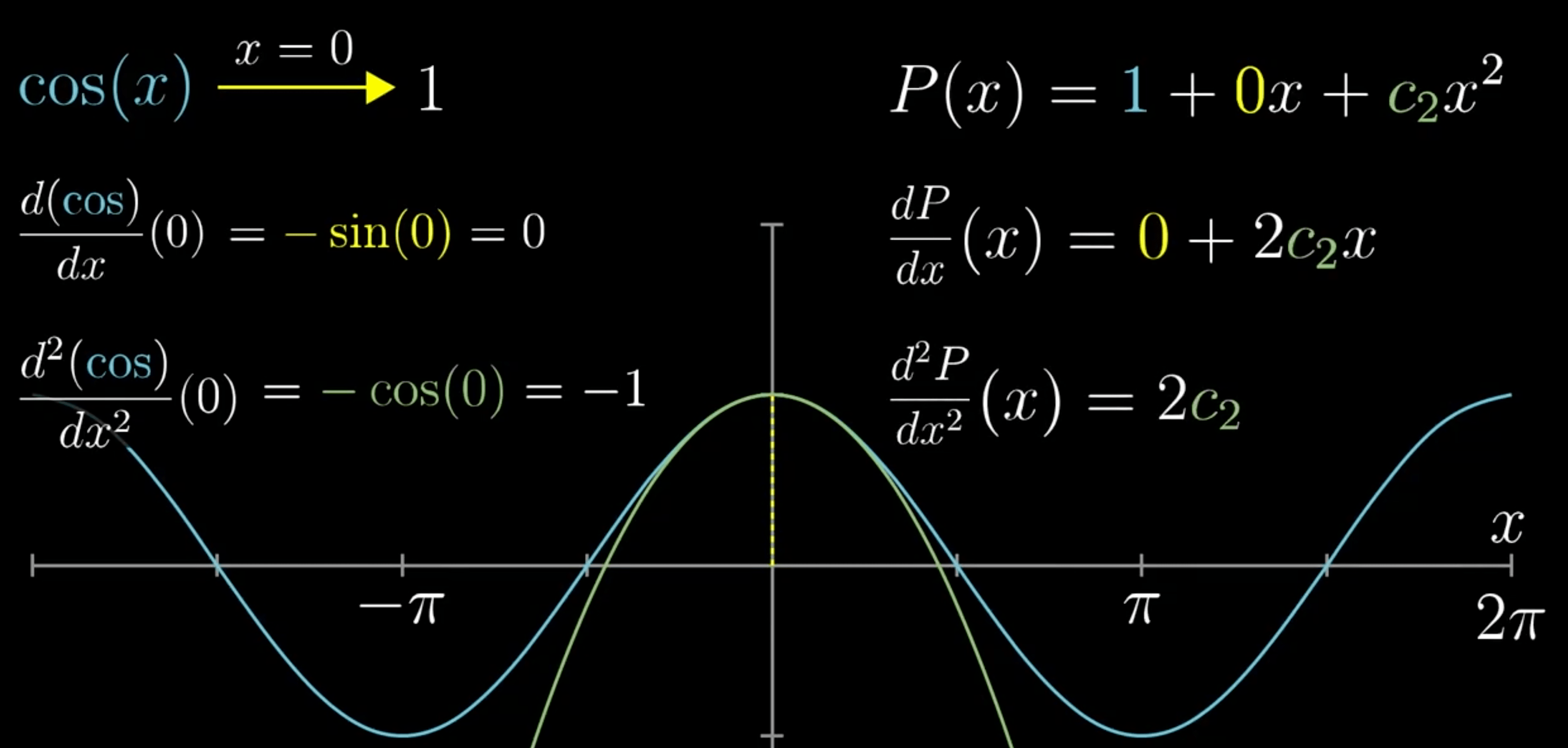
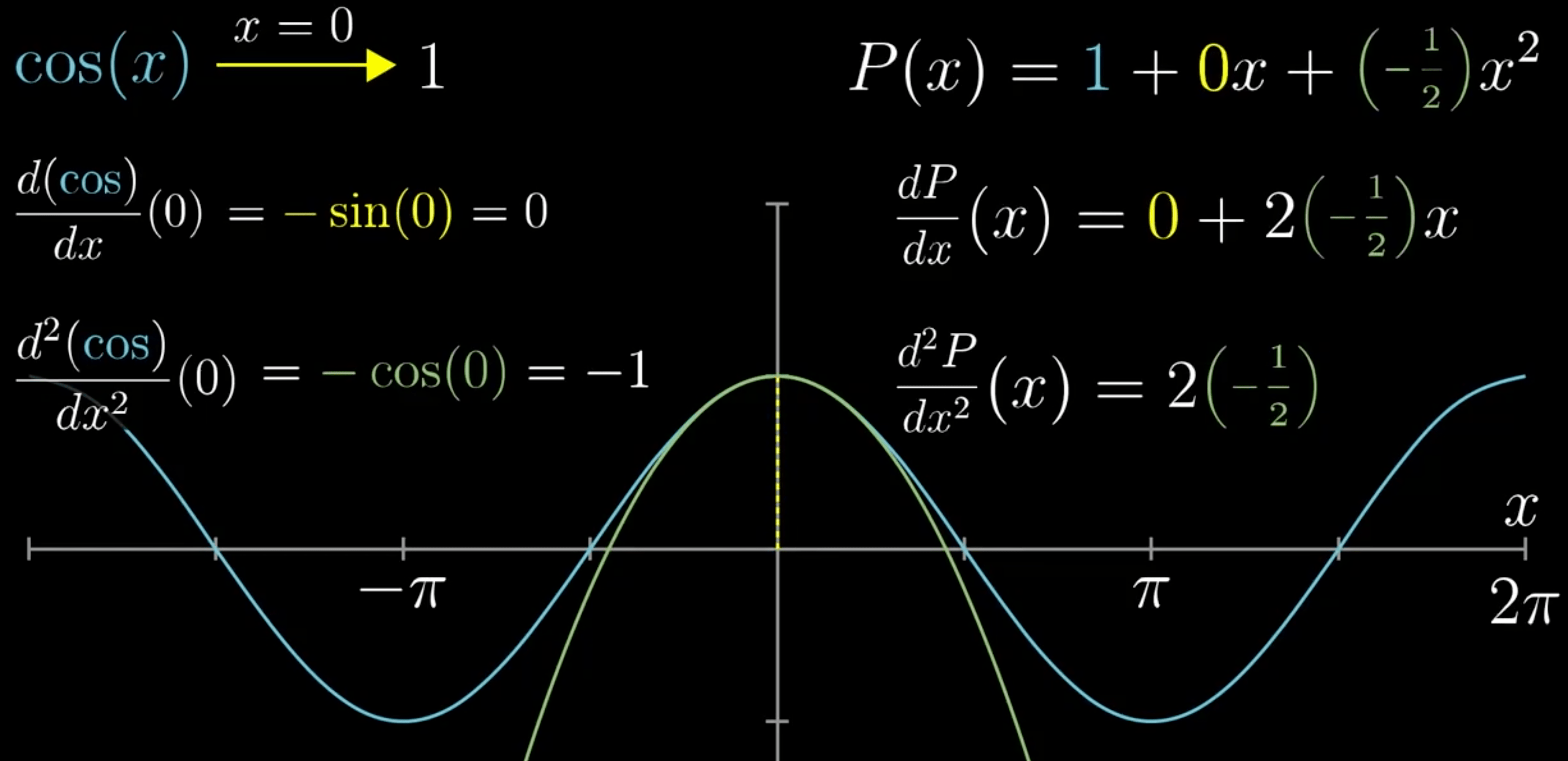
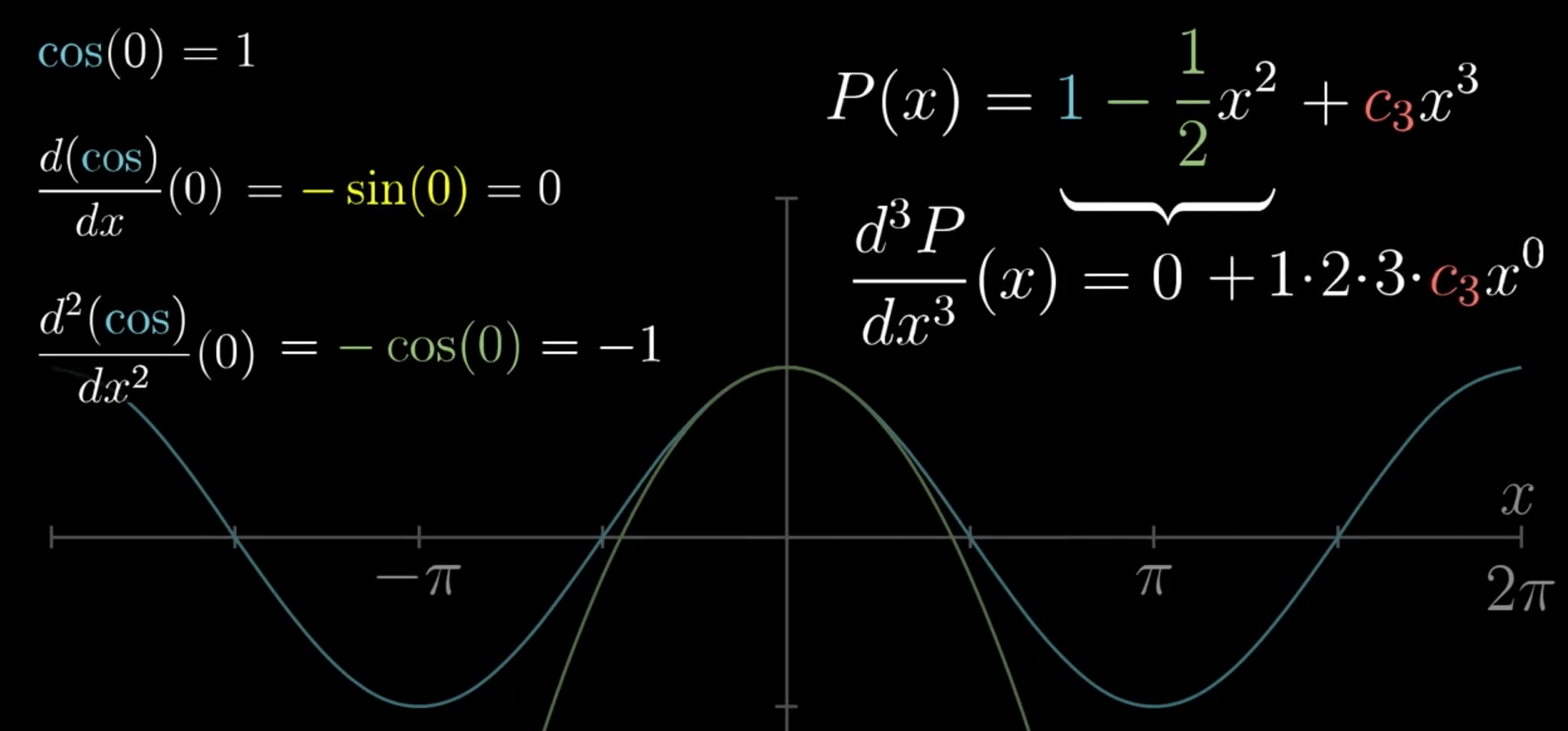
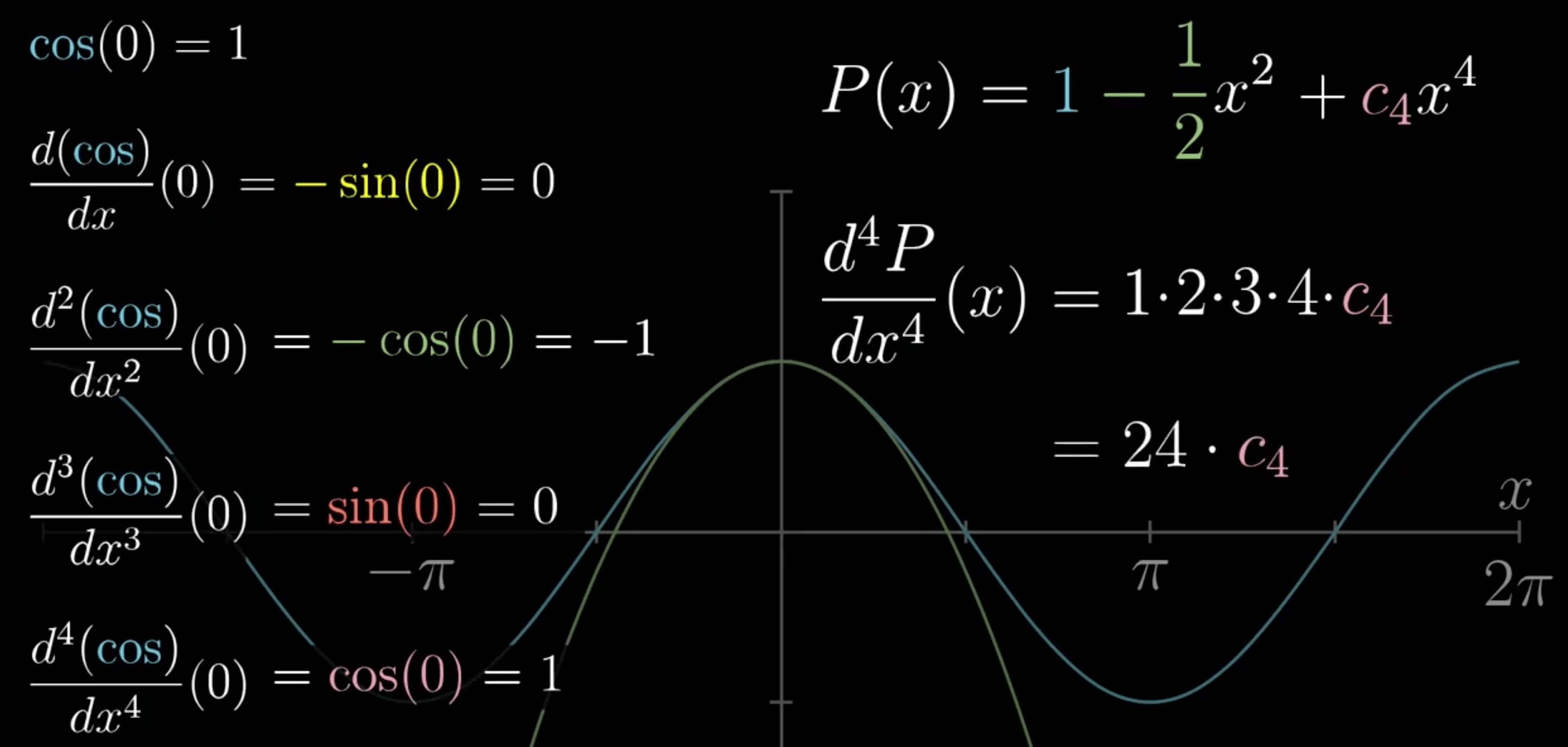
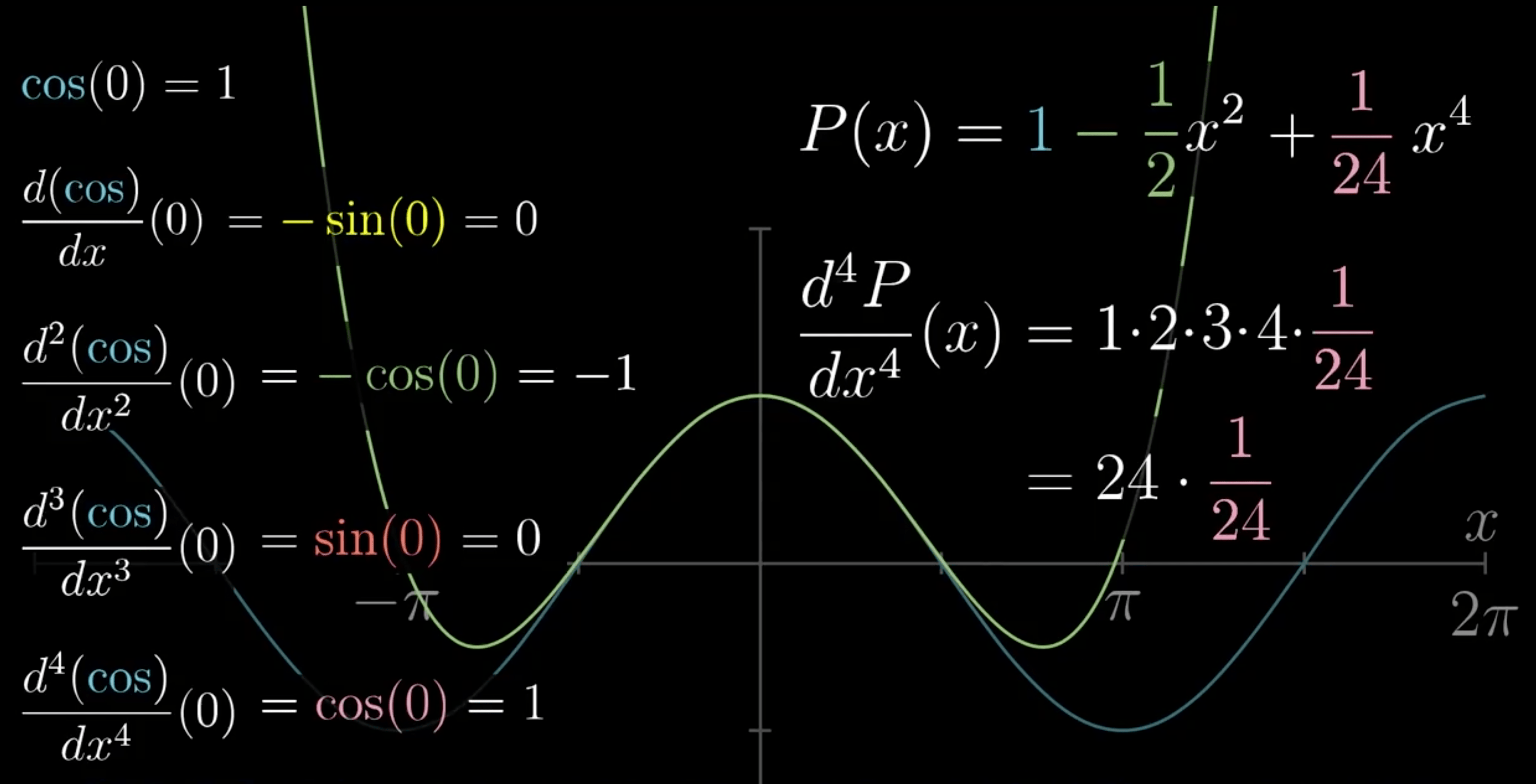
- \(c_{0}\):多项式在 x=0 处与 cos(0) 相等
- \(c_{1}\):两者导数一致
- \(c_{2}\):两者二阶导数一致

控制
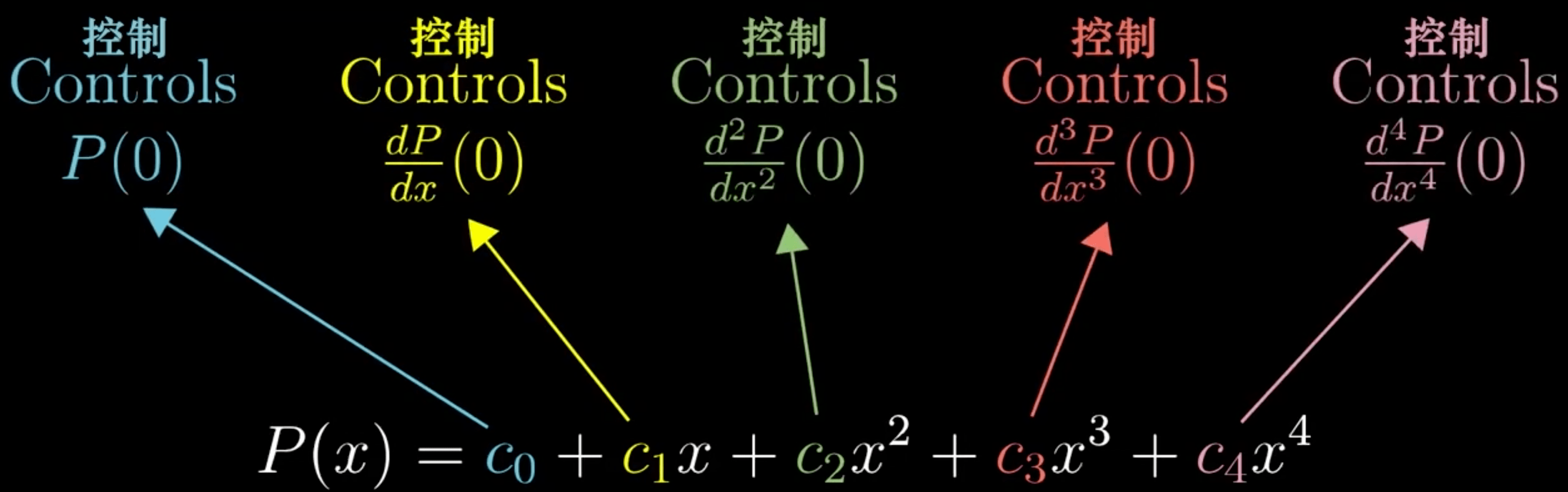
泰勒多项式
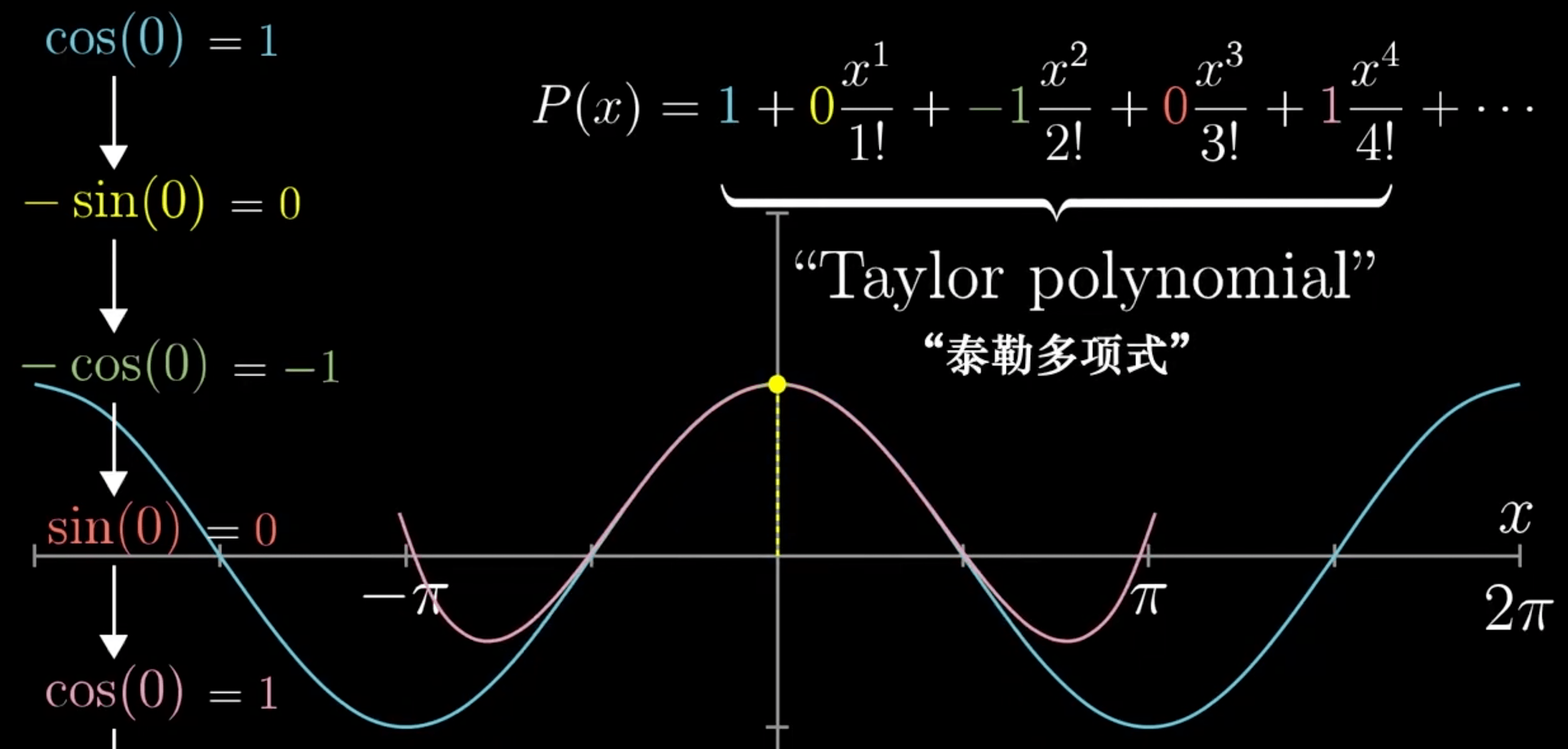
泰勒公式

\(e^{x}\) 泰勒多项式
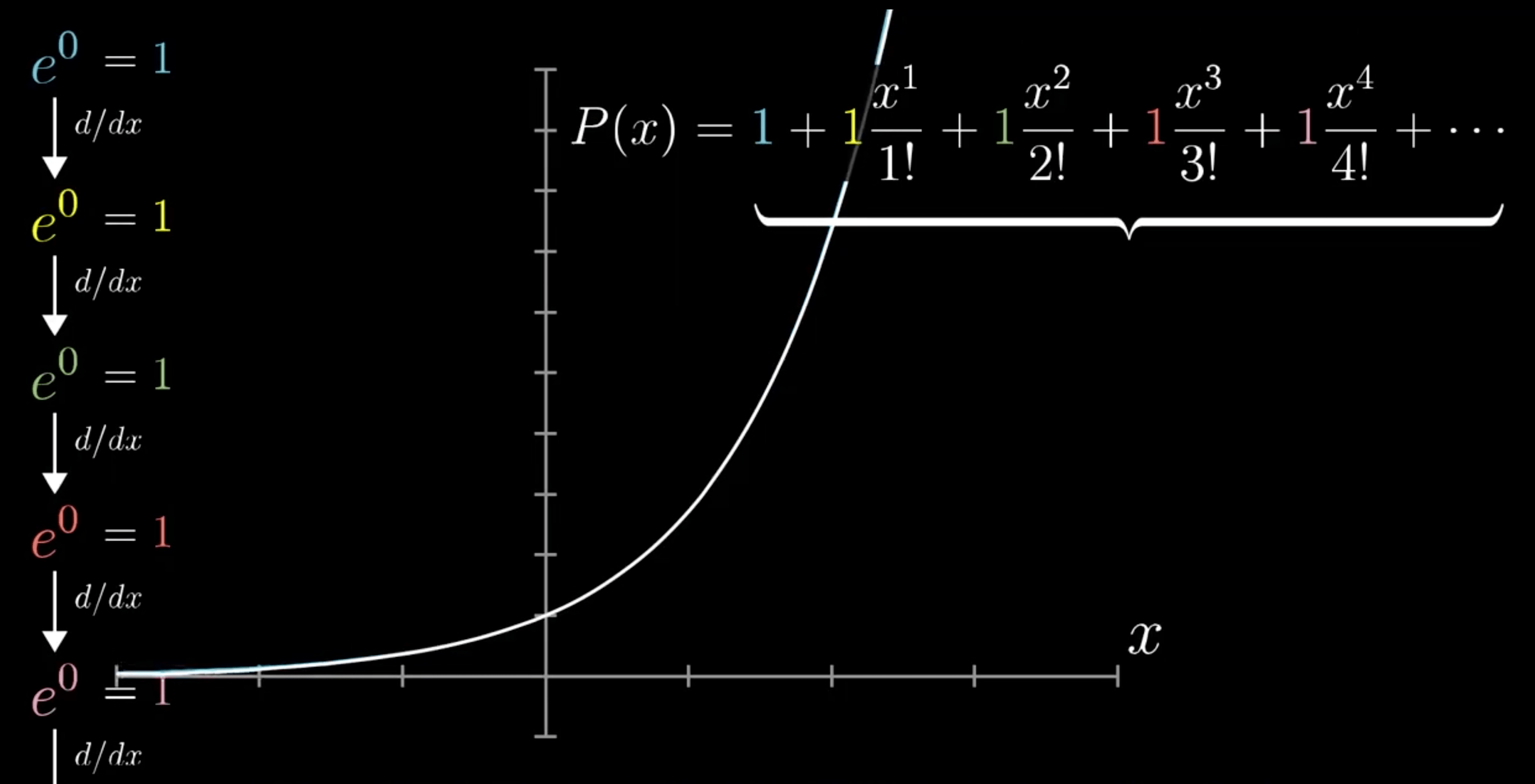
几何表示
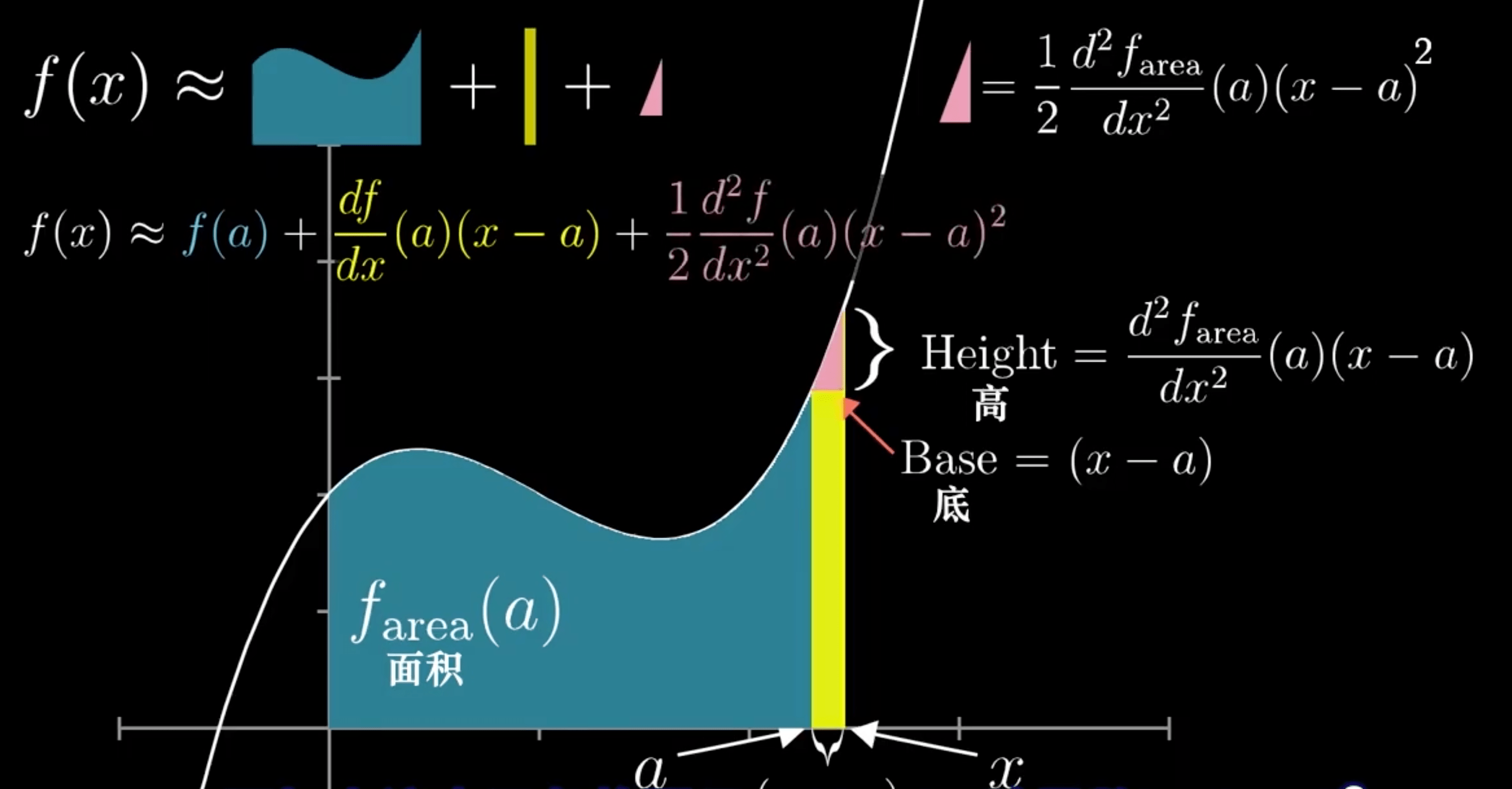
泰勒级数
- 泰勒多项:有限多项
- 泰勒级数:无阶多项
收敛
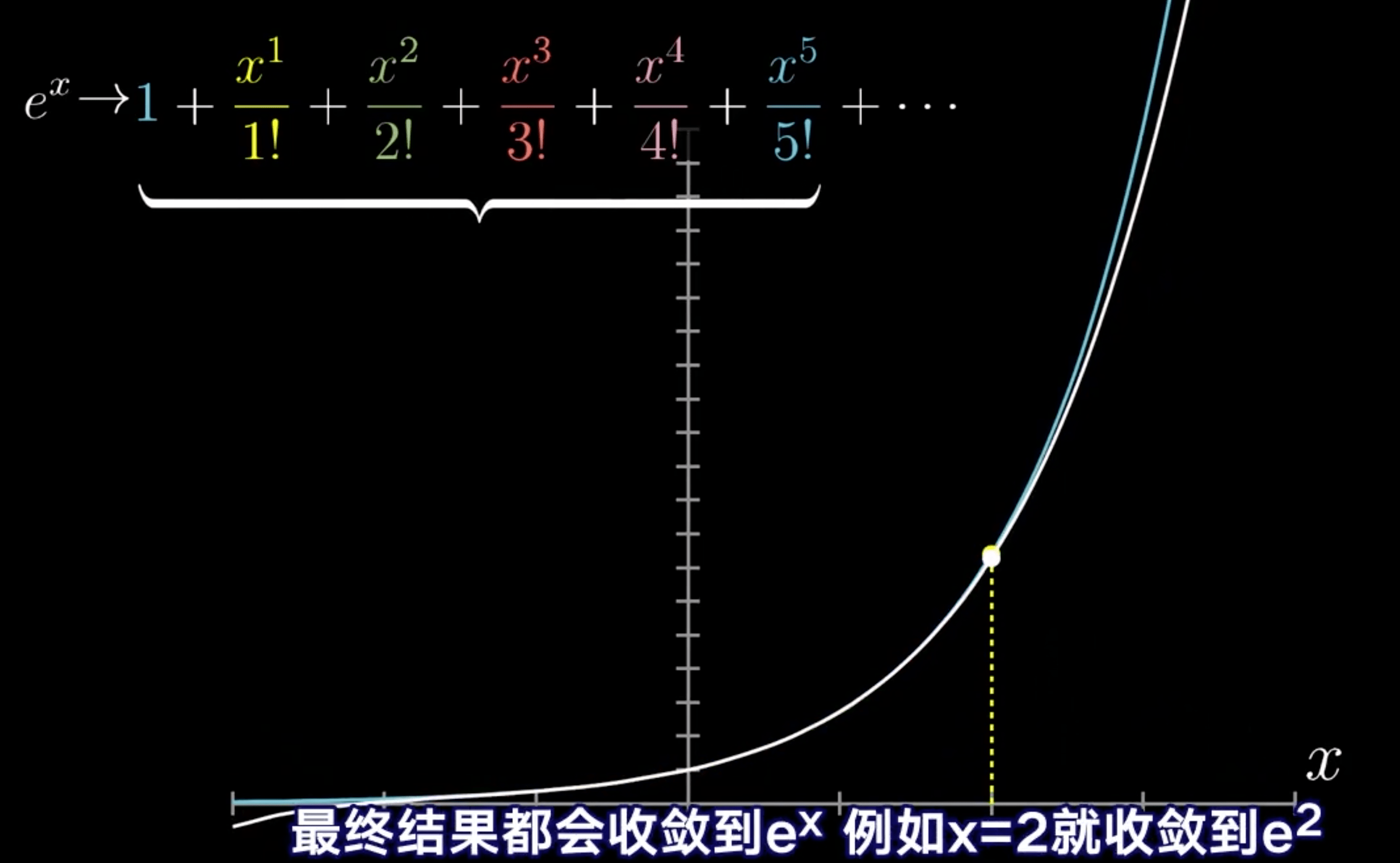
发散
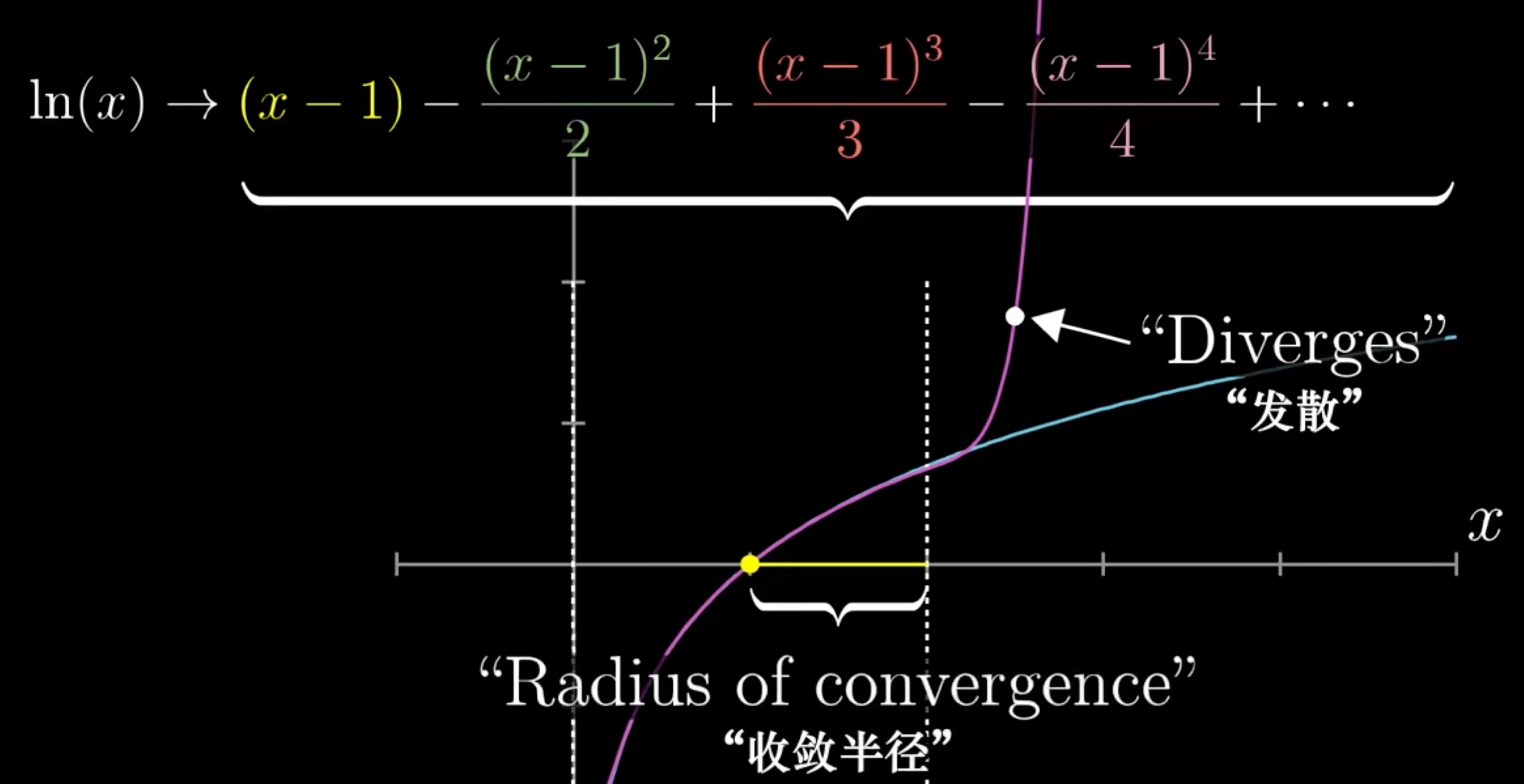
11. 你在微积分课上学不到的知识
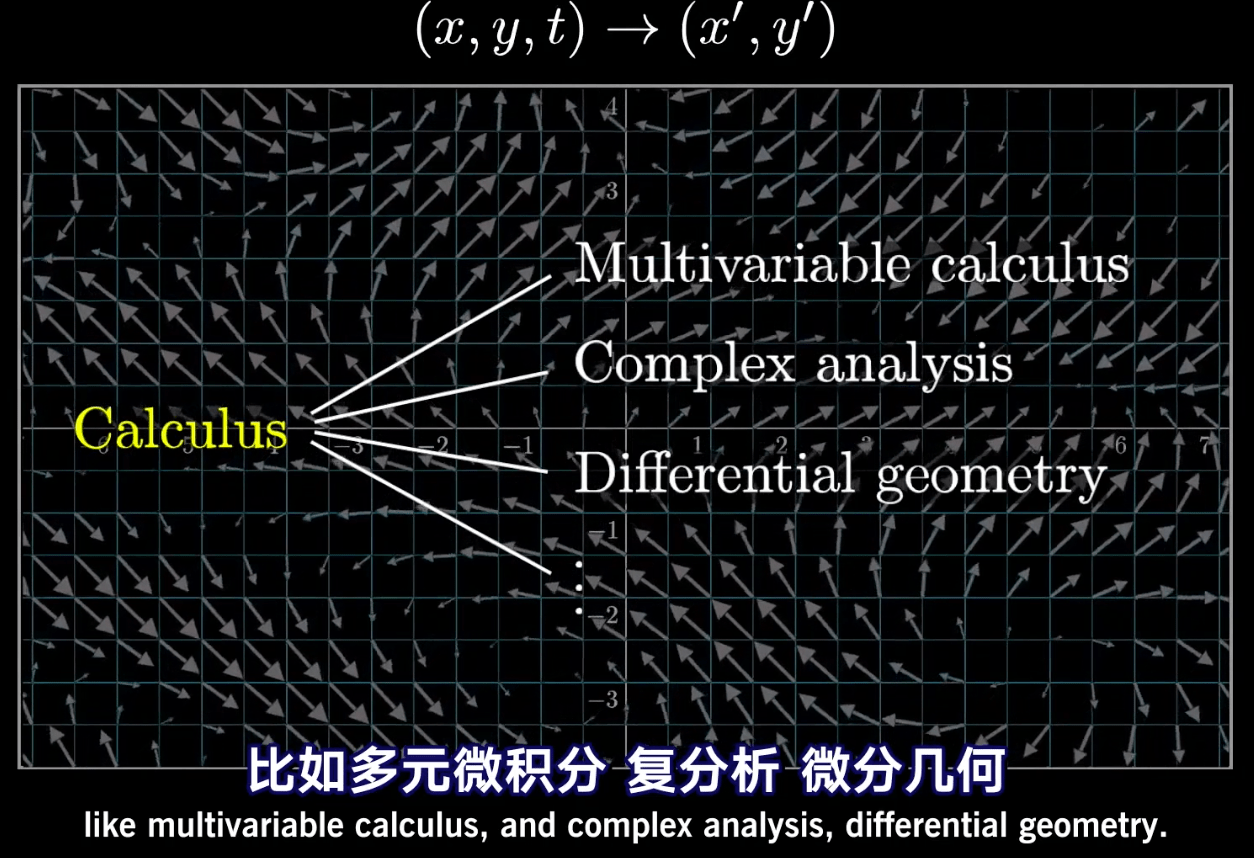
在这里观看完整的“微积分的本质”播放列表:<hhttp://3b1b.co/calculus>