
向量
空间的一组基的严格定义是这样的:
张成该空间的一个线性无关向量的集合
- 单个向量:箭头表示
- 多个向量:点表示

变换
\[ 变换 == 函数 \]
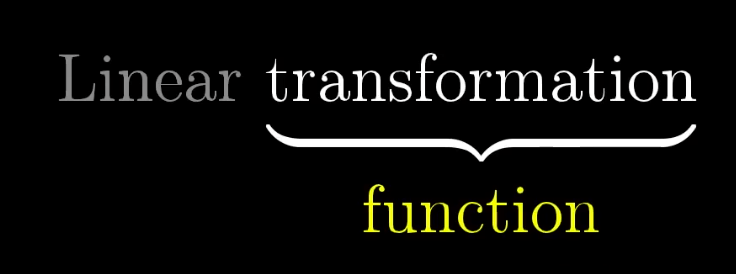
\[ y = f(x) \]
- IN: 向量(x)
- OUT: 向量(y)
为什么叫 变换
因为使用“变换”是在暗示以特定方式来可视化这一输入-输出关系
运动 => 向量的函数
线性变换
- 直线在变换后仍然保持为直线,不能有所弯曲
- 原点必须保持固定
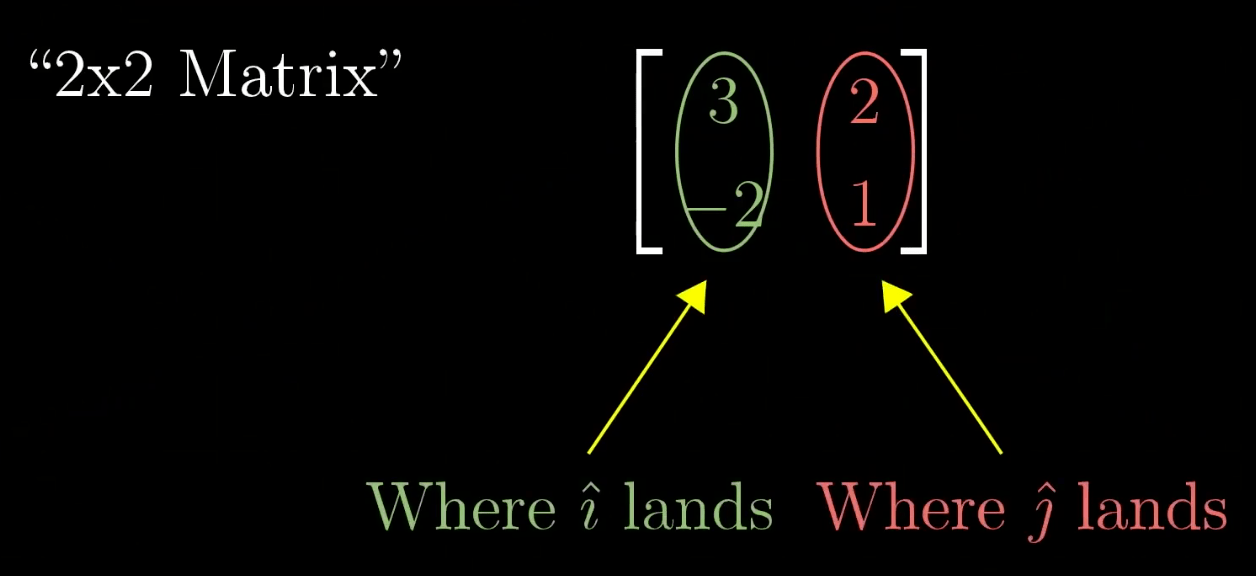
基向量
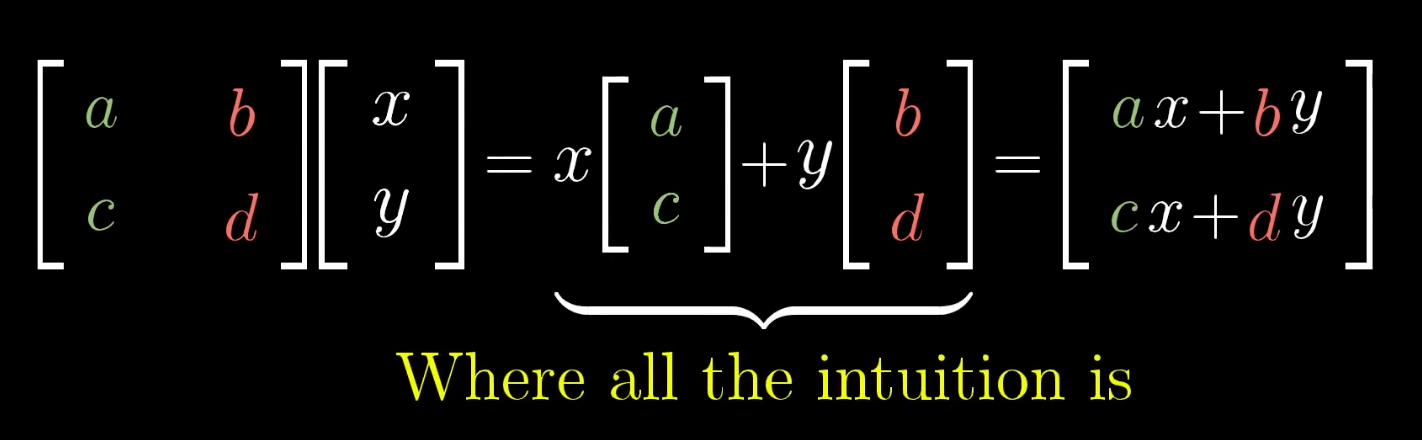
矩阵乘法
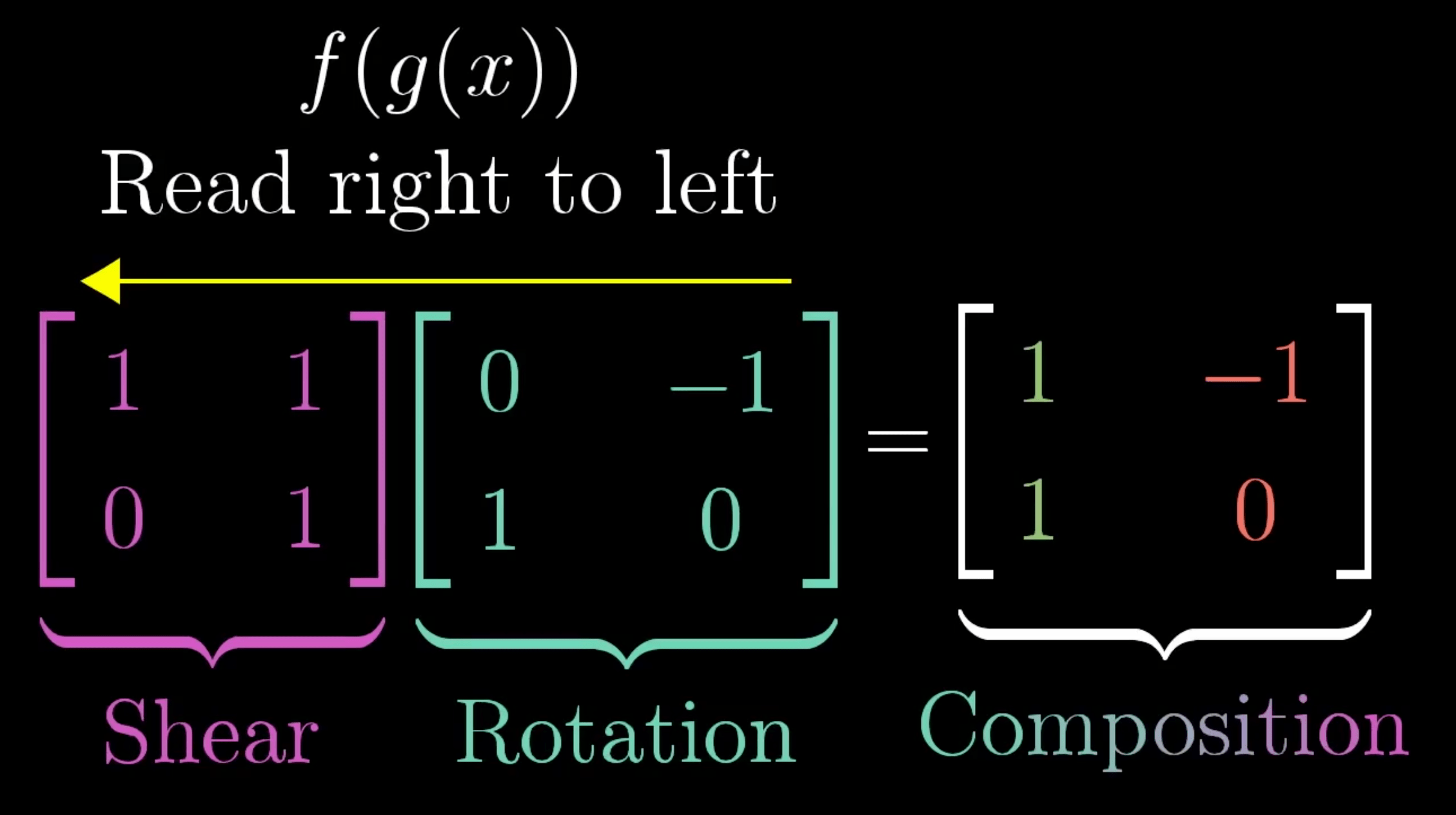
复合变换 -> 复合函数
行列式
线性变换改变面积的比例。
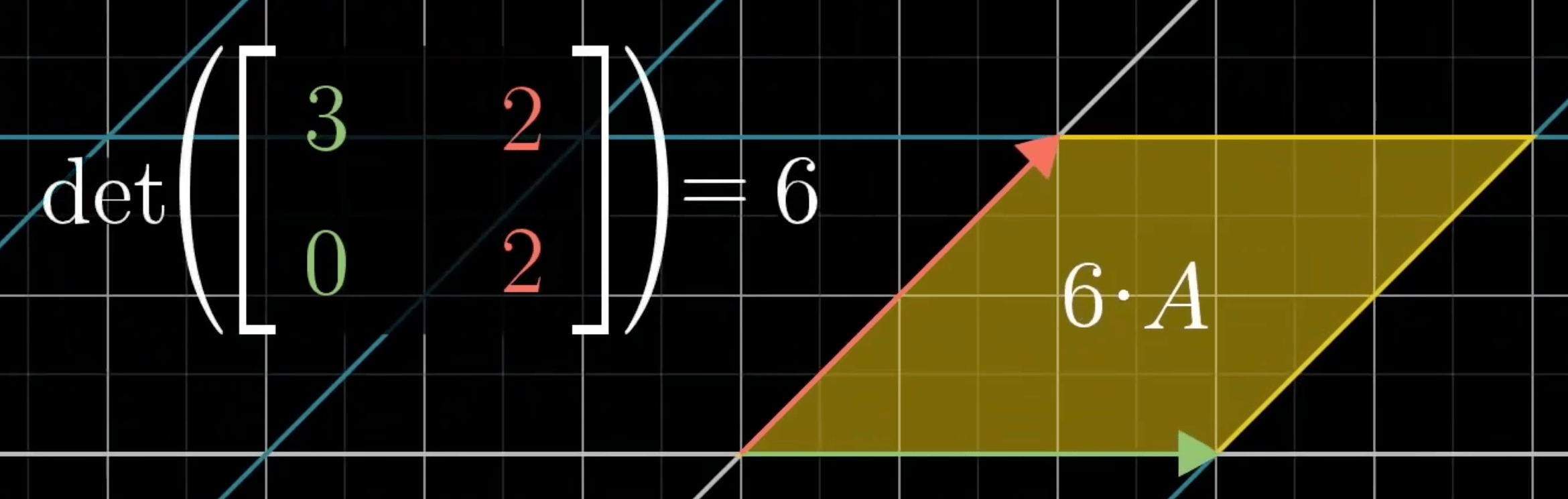
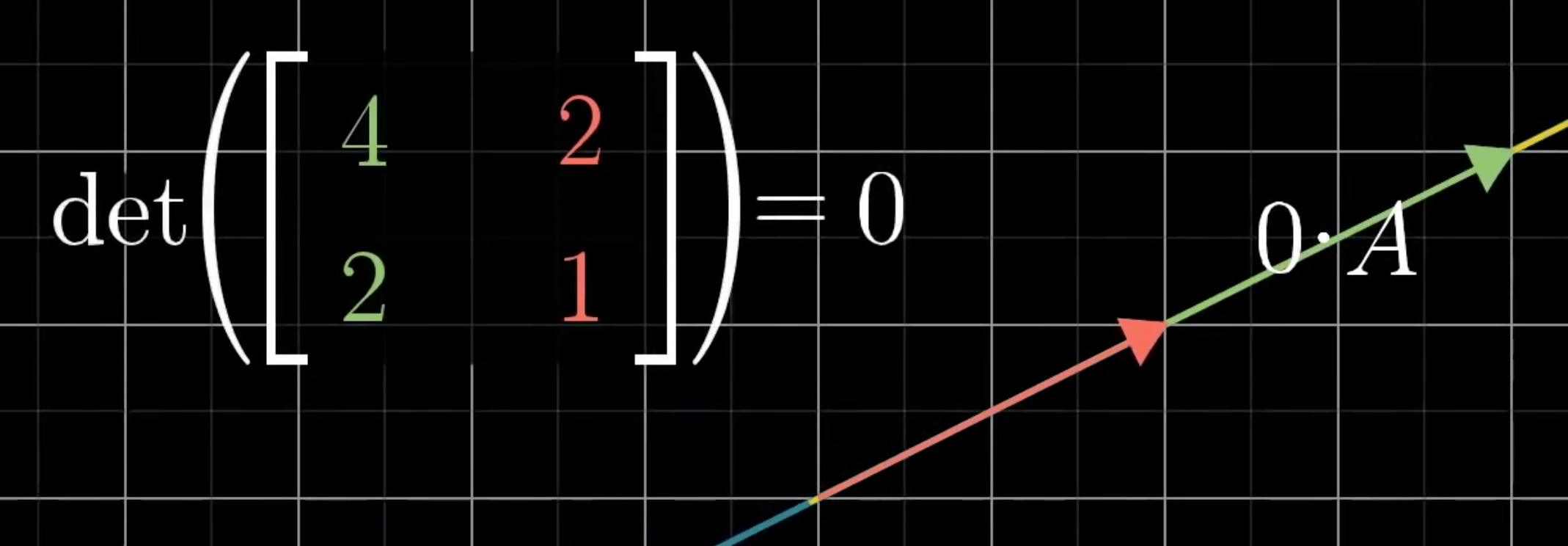
- 行列式为 \(0\) => 空间压缩到更小的维度
- 当空间定向改变的情况发生时,行列式为
负
计算行列式
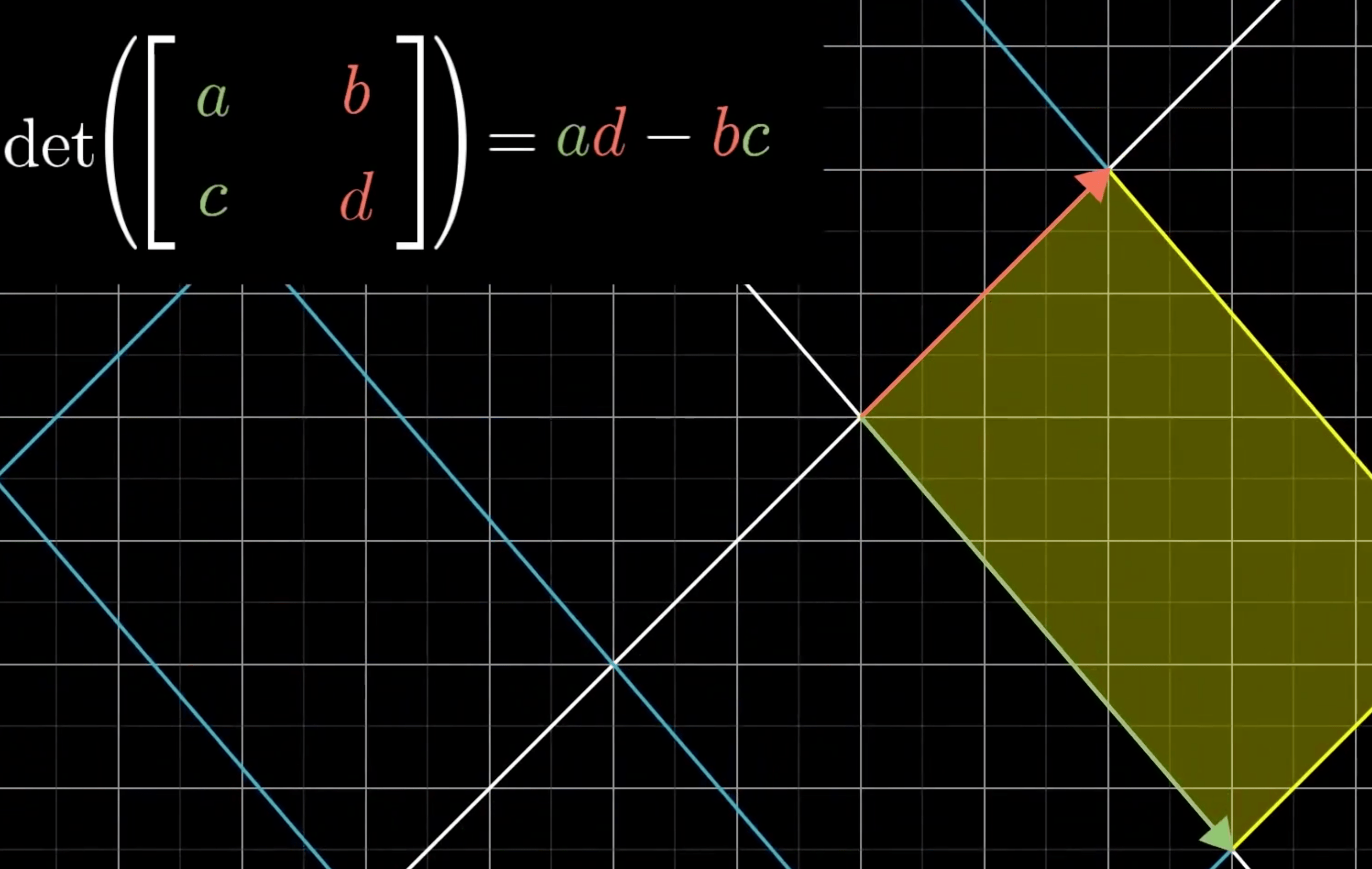
- \(a\): \(x\) 轴伸缩比例
- \(b\): 对角方向 拉伸/压缩 比例
- \(c\): 对角方向 拉伸/压缩 比例
- \(d\): \(y\) 轴伸缩比例
二阶行列式
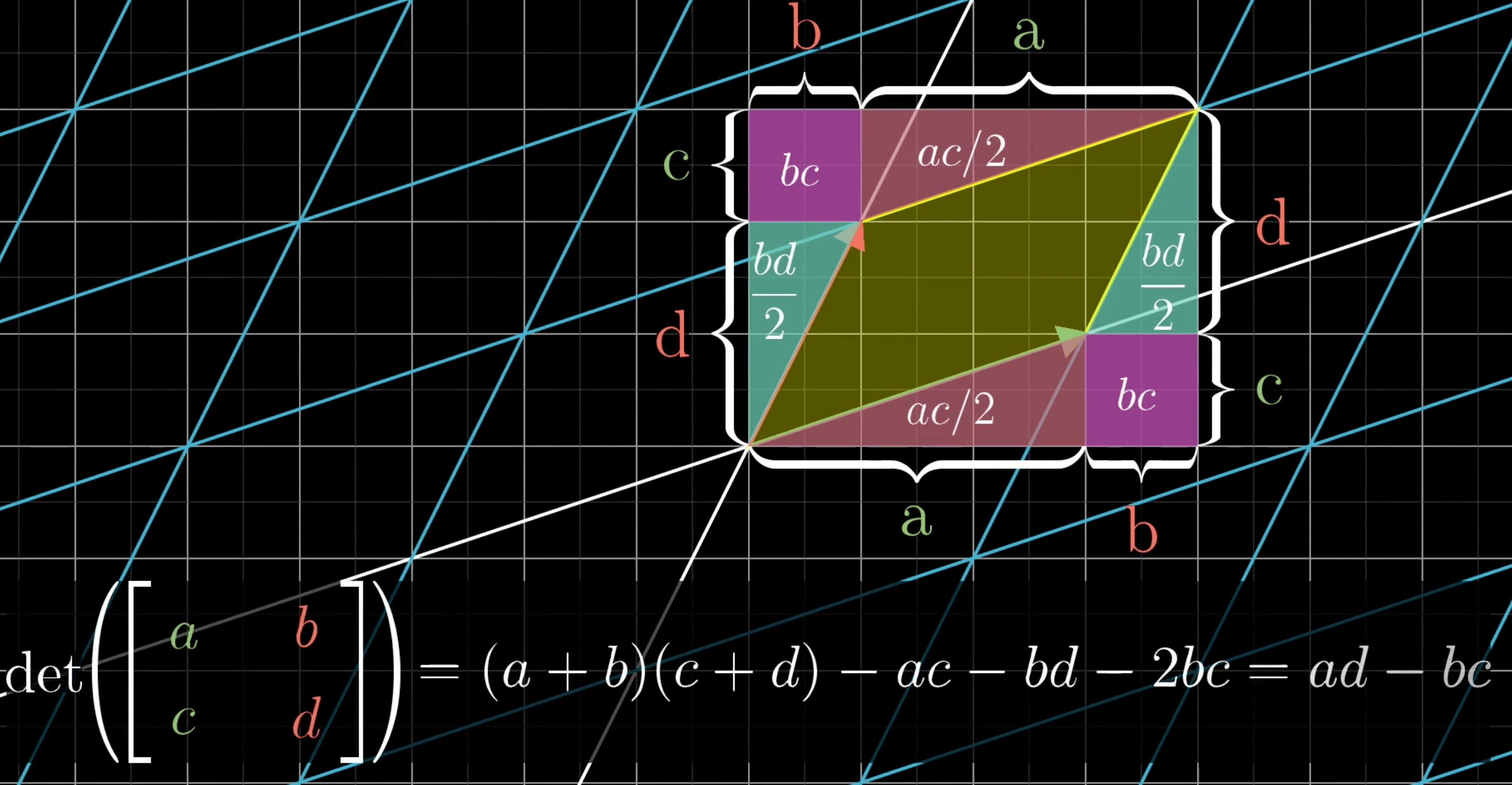
三阶行列式
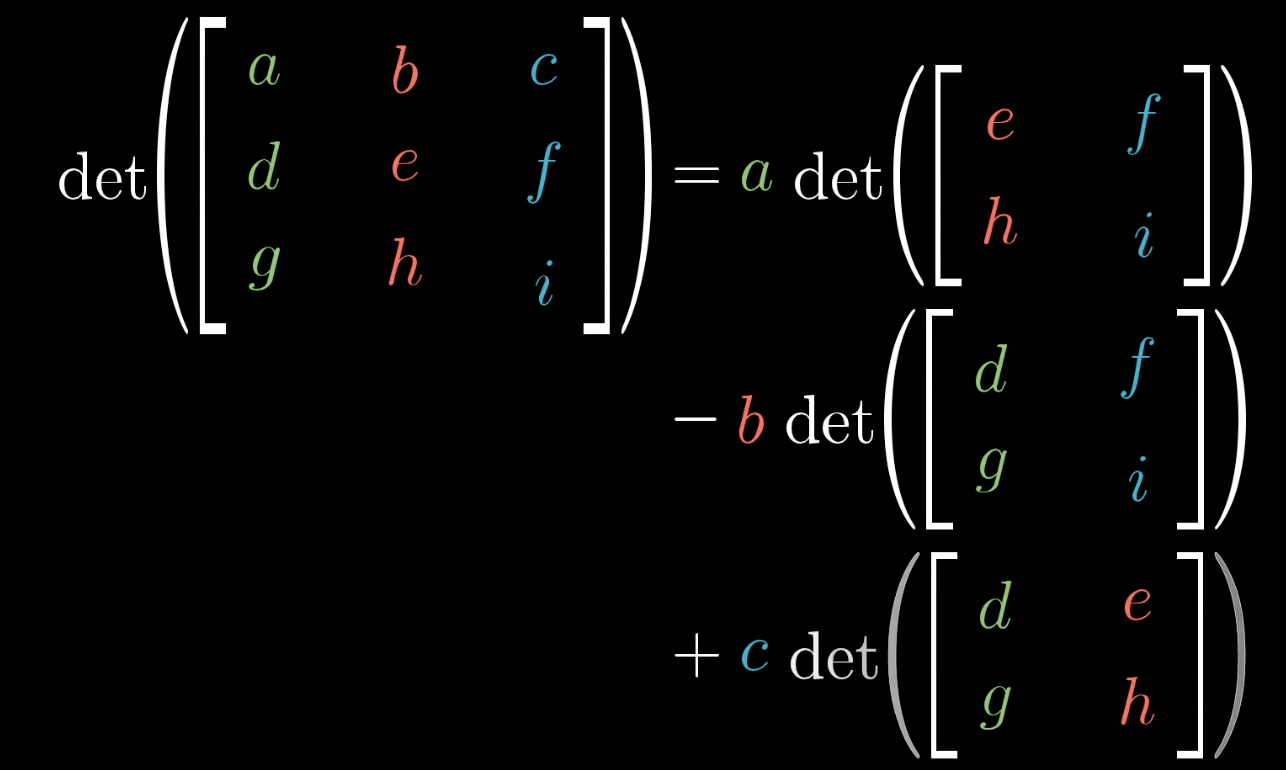
平行六面体的体积
矩阵
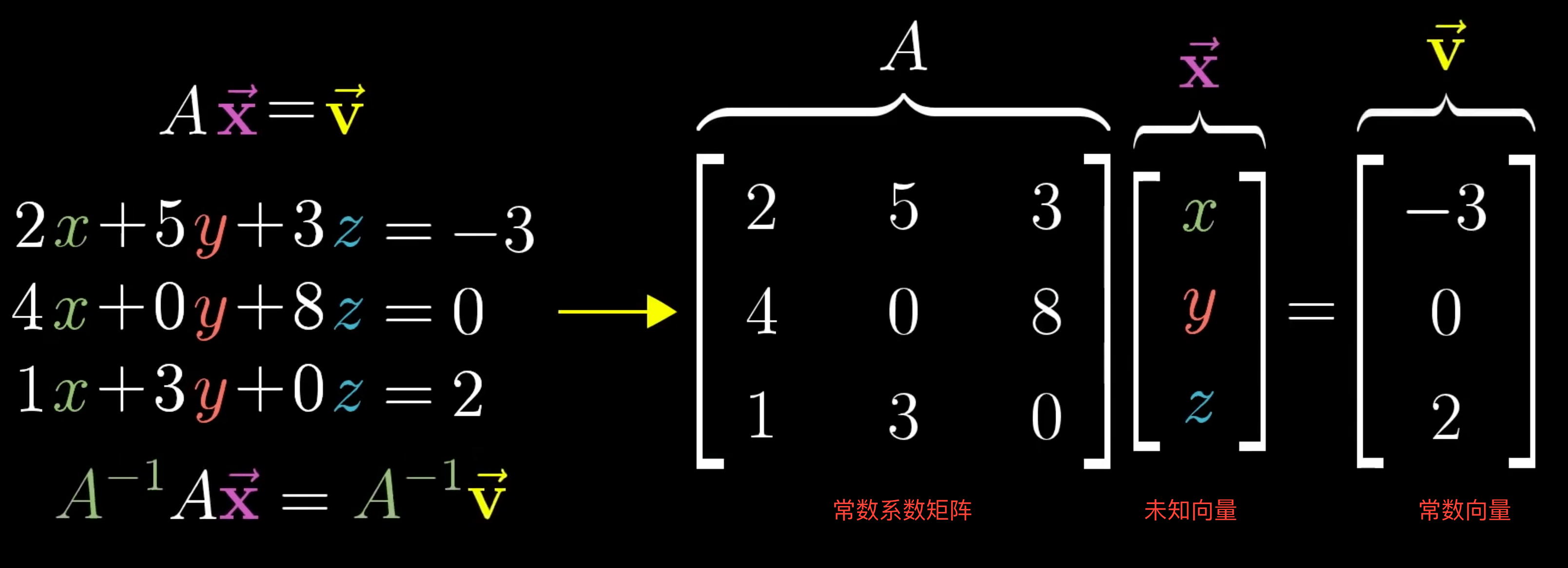
\(A\) 代表变换矩阵
逆矩阵
恒等变换:单位矩阵
\[ A^{-1}A = I \]
逆乘以 \(A\)
列空间:矩阵的列所张成的空间秩:列空间的维数(变换后空间的维数)
矩阵乘法
变换矩阵
行:变换后的独立坐标列:变换前的基向量零空间/核:变换后落在原点的向量的集合
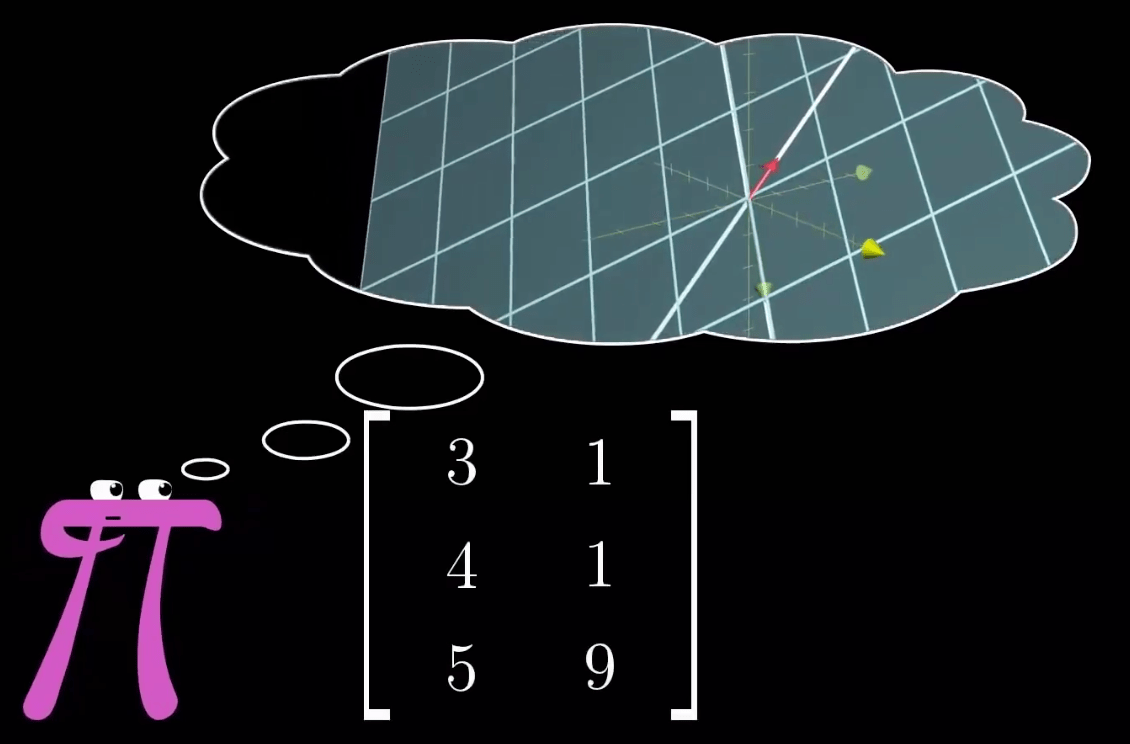
2 列 -> 3 行
=>
2 维 -> 3 维
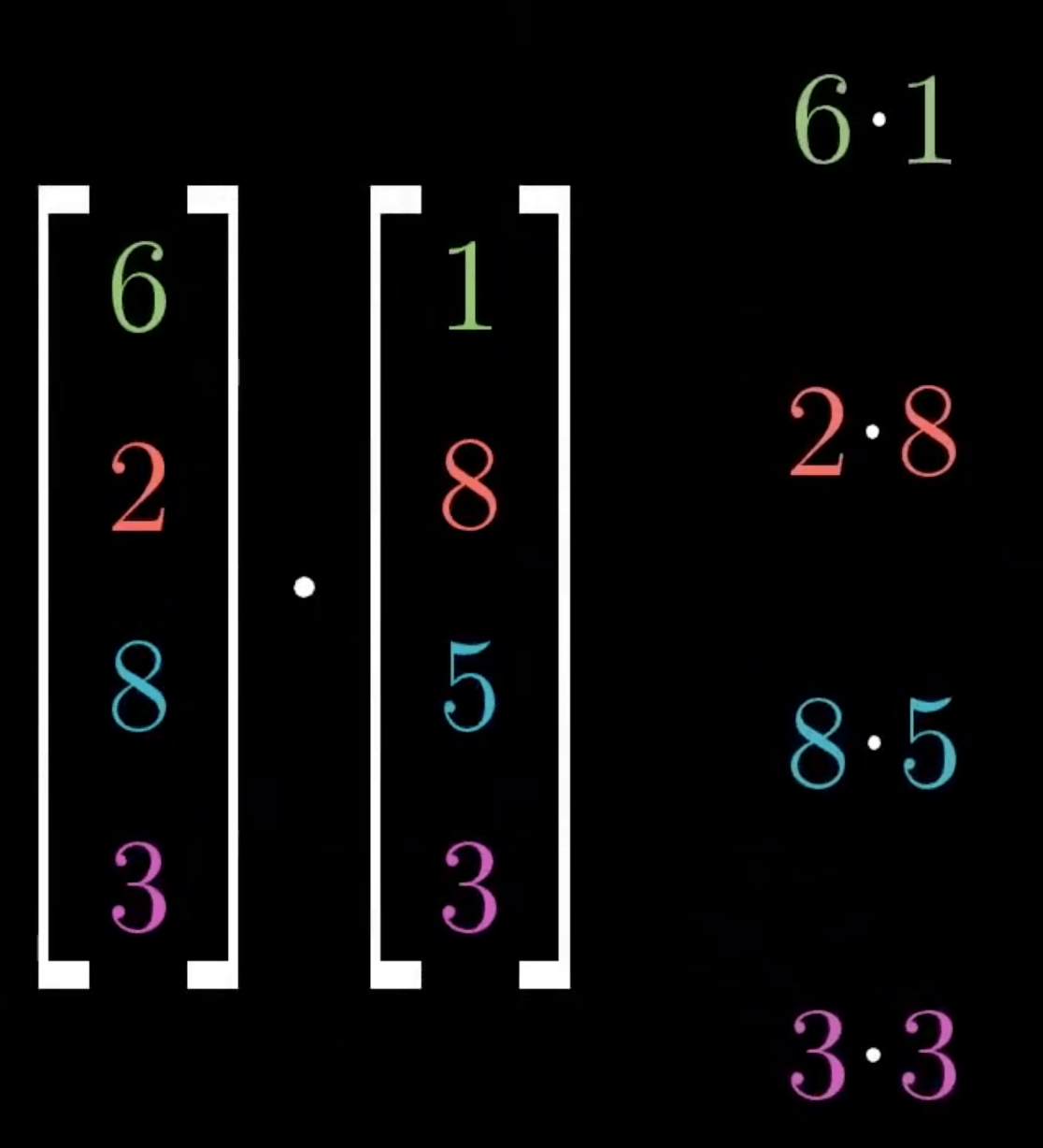
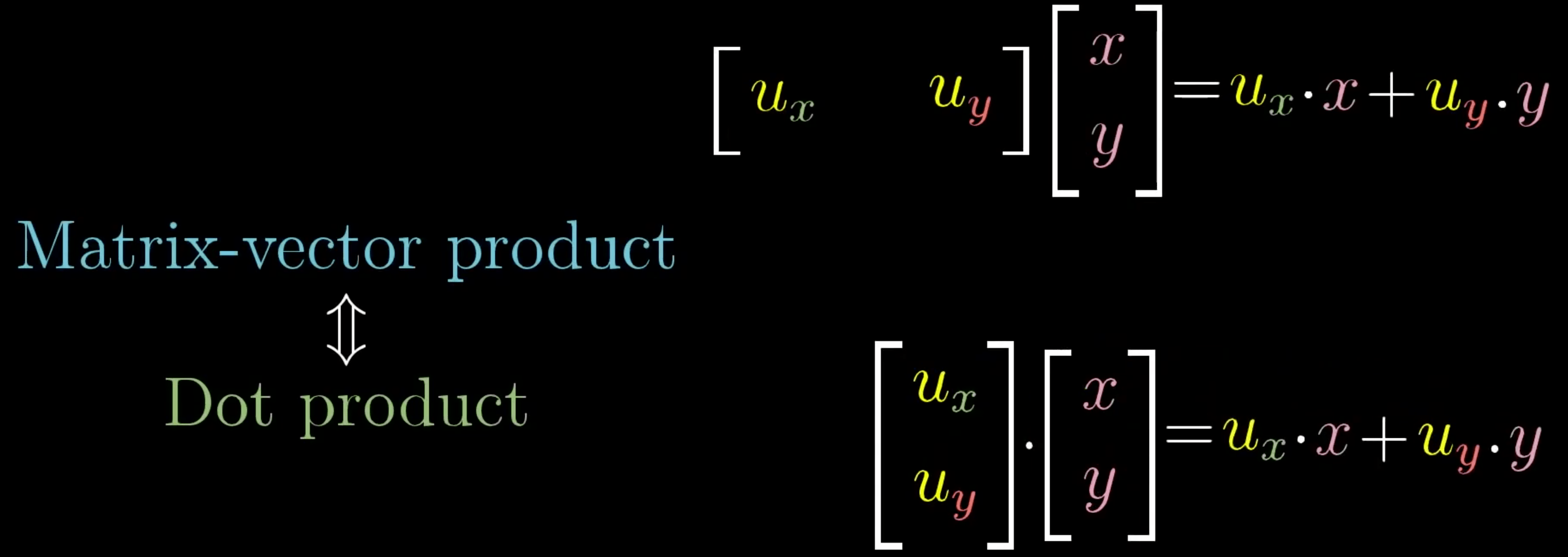
点积(数量积/标量积)
一种接受两个等长的数字序列(通常是坐标向量)、返回单个数字的代数运算
- 内积:两个笛卡尔坐标向量的点积常称为内积
代数定义
\[ \vec{a} \cdot \vec{b} = \sum_{i=1}^n a_ib_i = a_1b_1 + a_2b_2 + \cdots + a_nb_n \]
\[ \vec{a} \cdot \vec{b} = \vec{a}\vec{b}^T \]
几何定义
\[ \vec{a} \cdot \vec{b} = |\vec{a}| \, |\vec{b}| \cos \theta \; \]
- \(|\vec{a}|\):模长
- \(\theta\):夹角
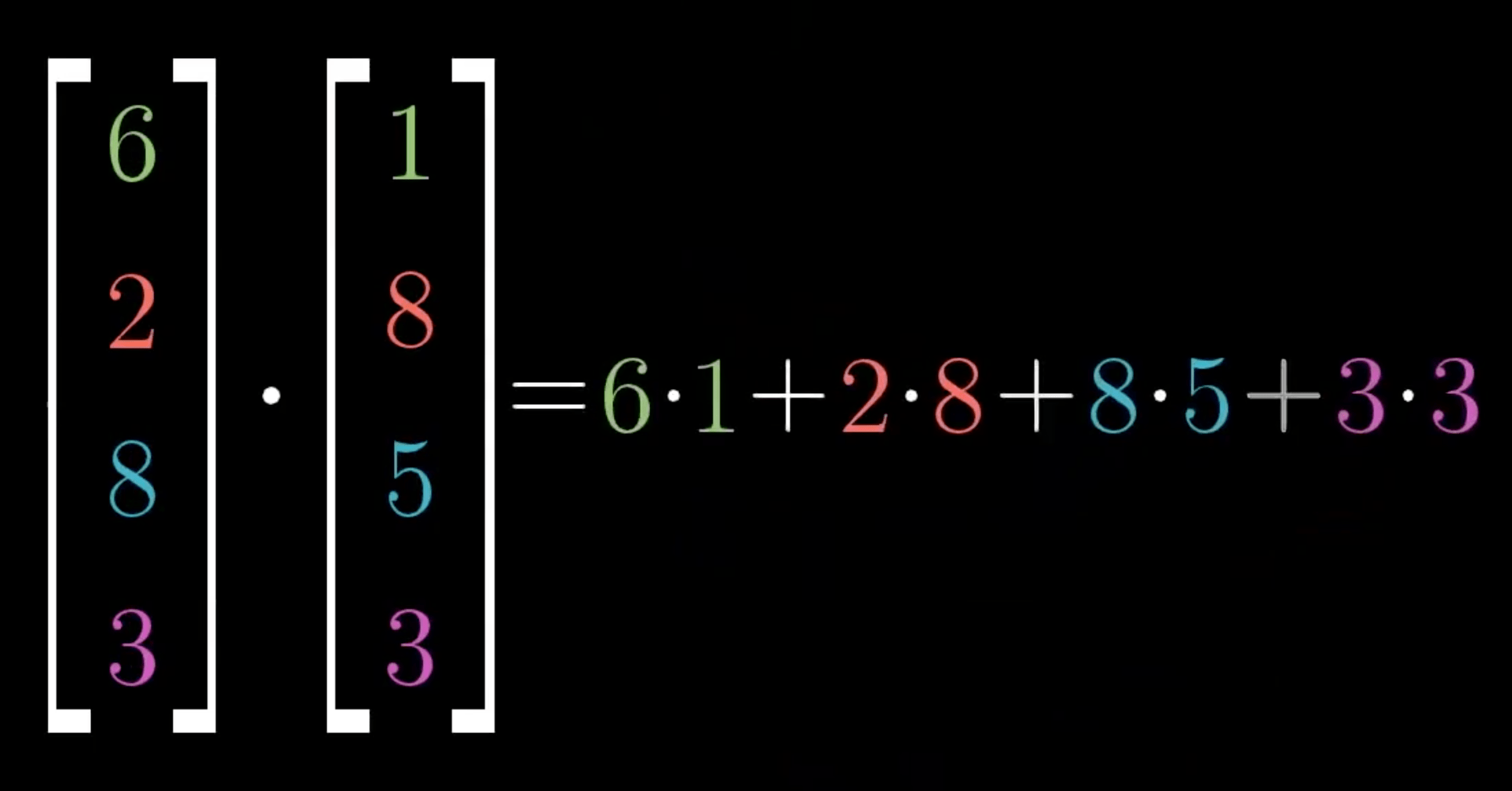
叉积
面积
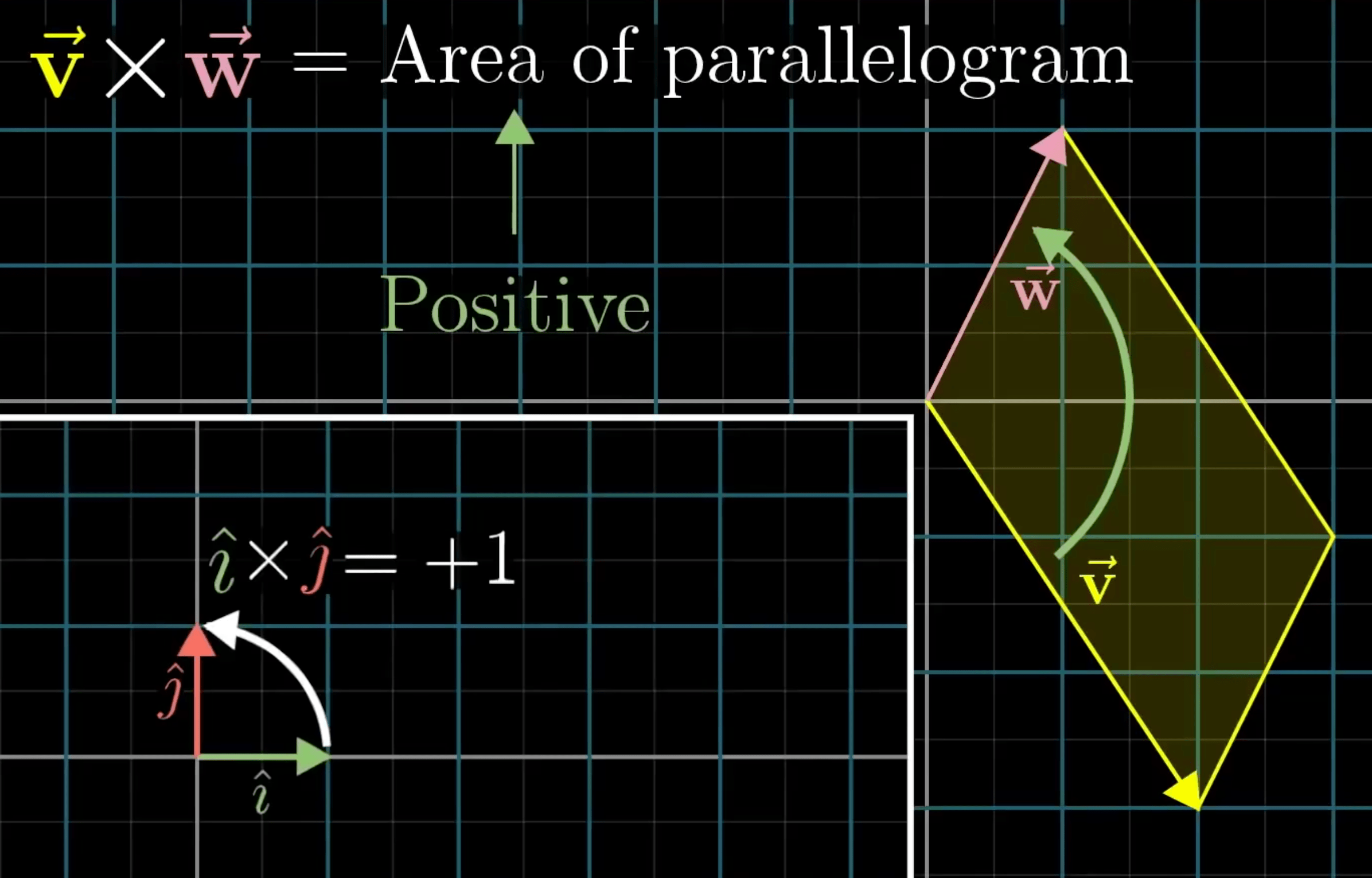
求行列式
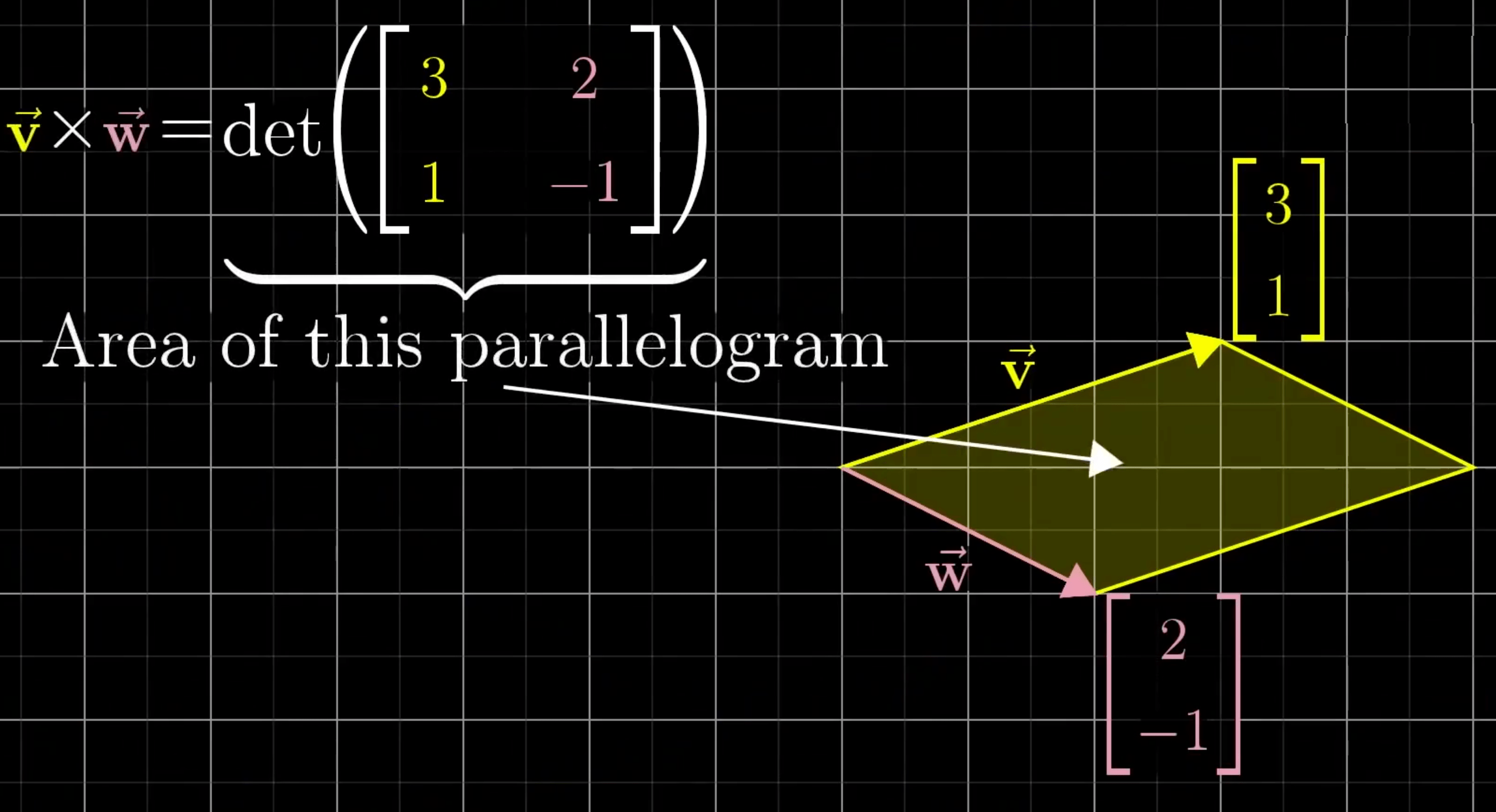
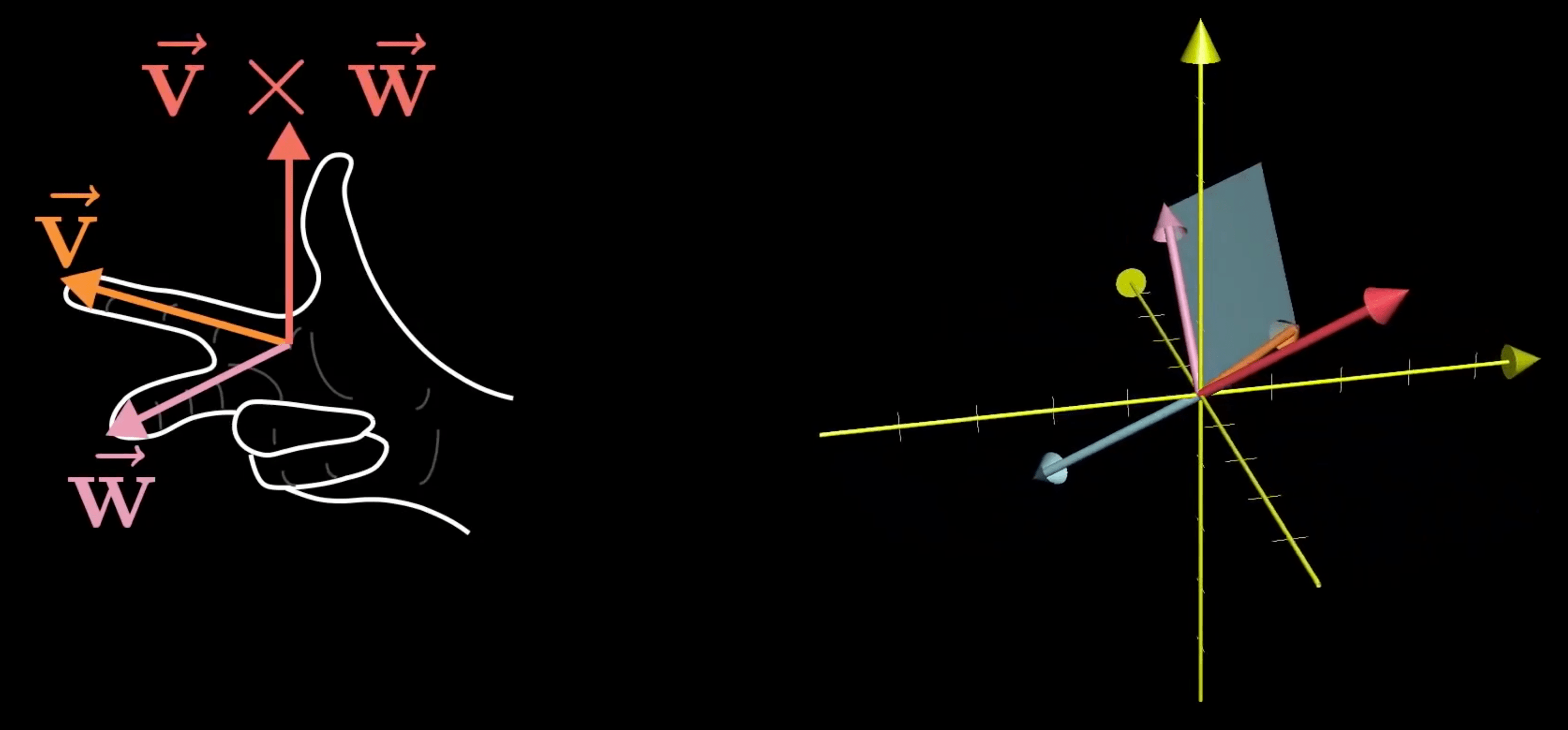
方向(右手定则)
特征向量 和 特征值 Eigenvectors and eigenvalues
- 特征向量:线性变换[a]之后,得到的新向量仍然与原来的向量保持在同一条直线上
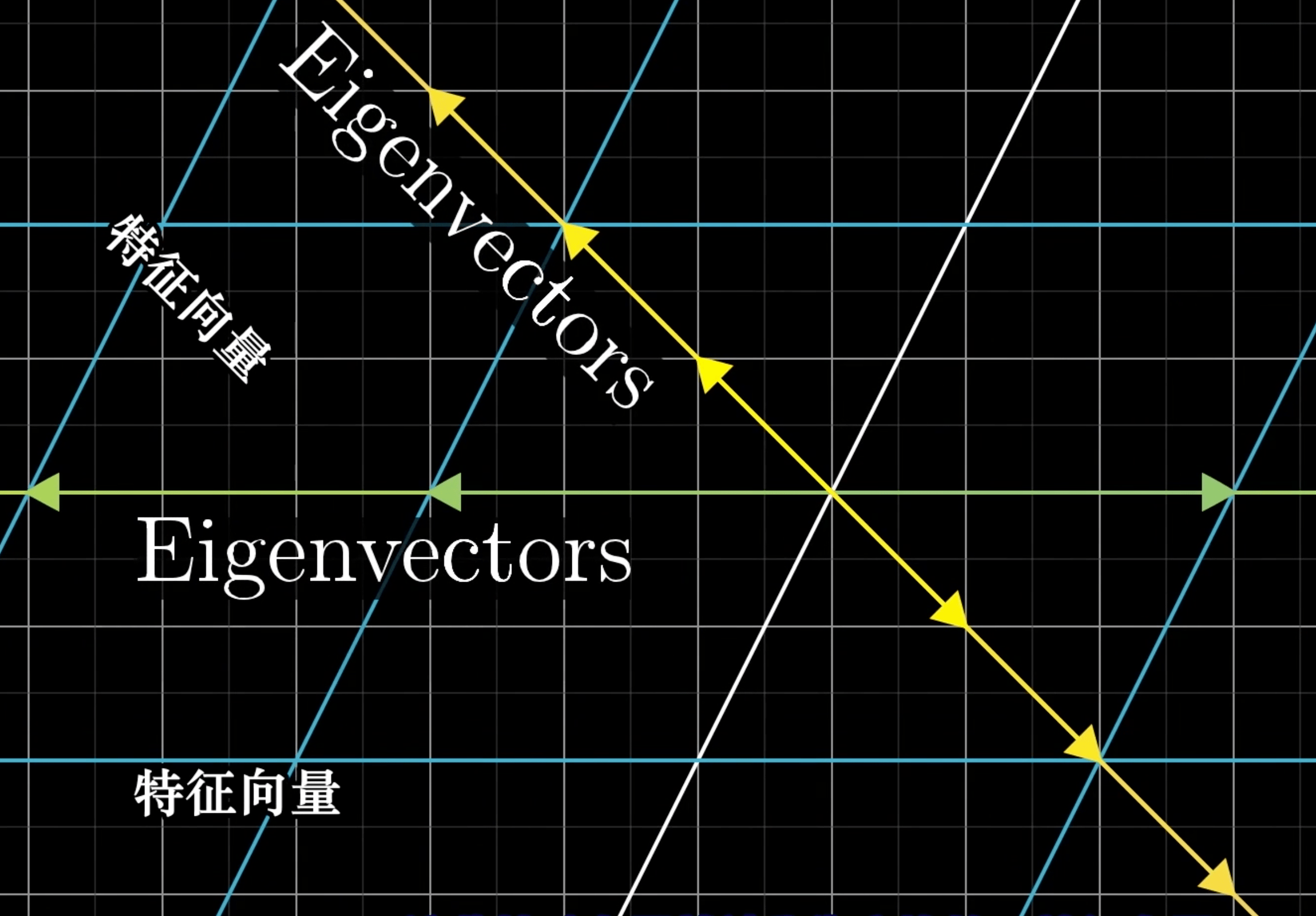
- 特征值:特征向量的长度在该线性变换下 缩放 的比例

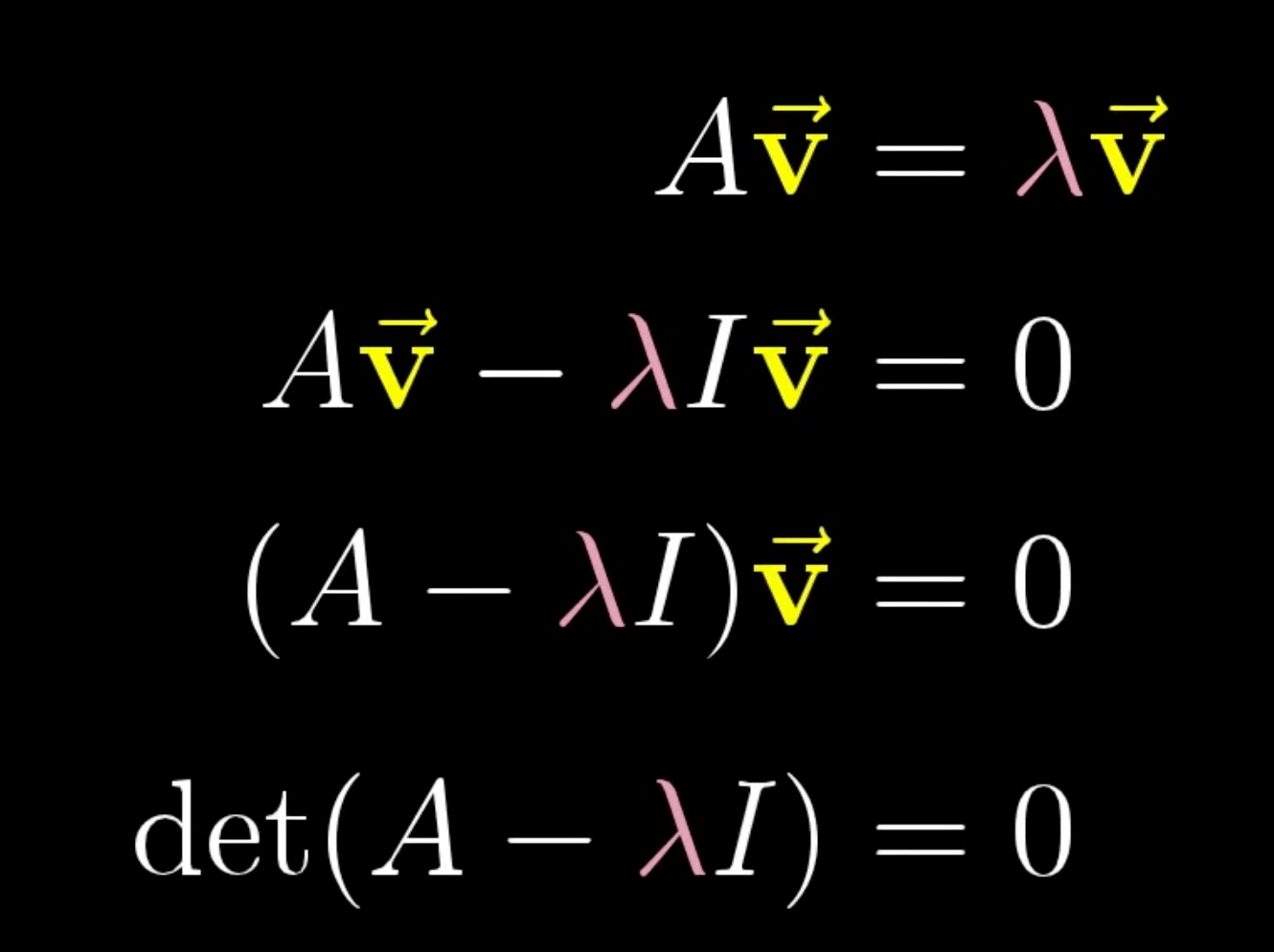
- 特征基:一组基向量(也是特征向量)构成的集合
抽象向量空间

函数 => 向量特性
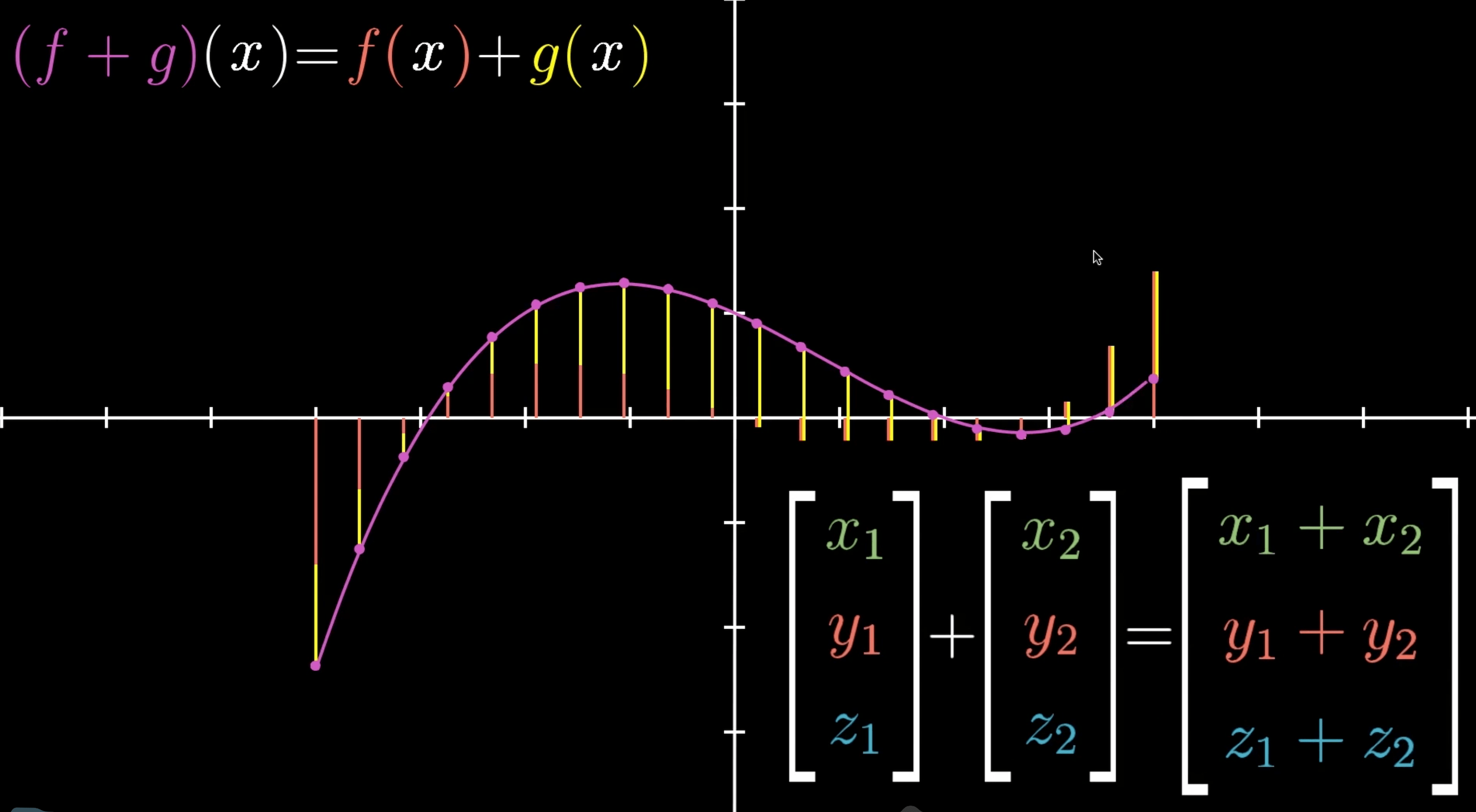
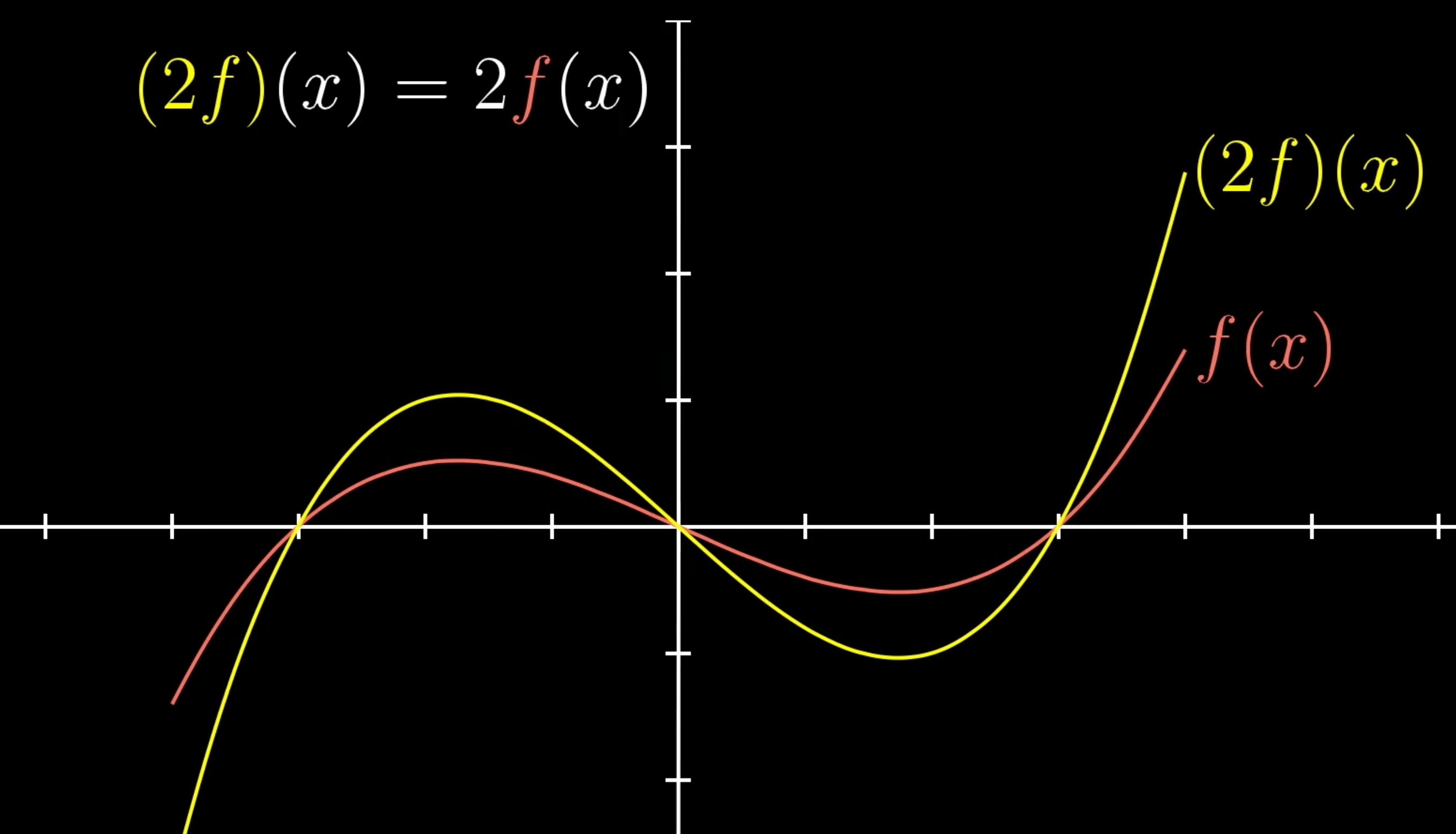
向量

函数
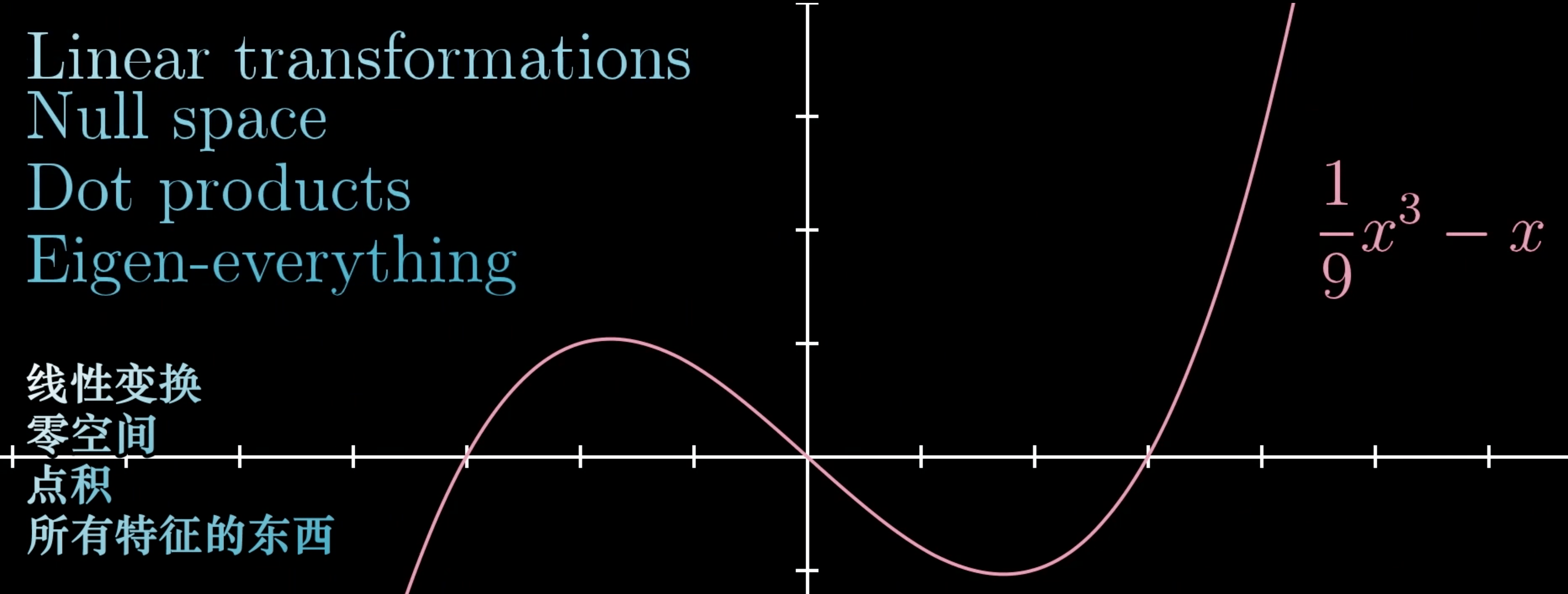
导数:函灵敏的线性变换
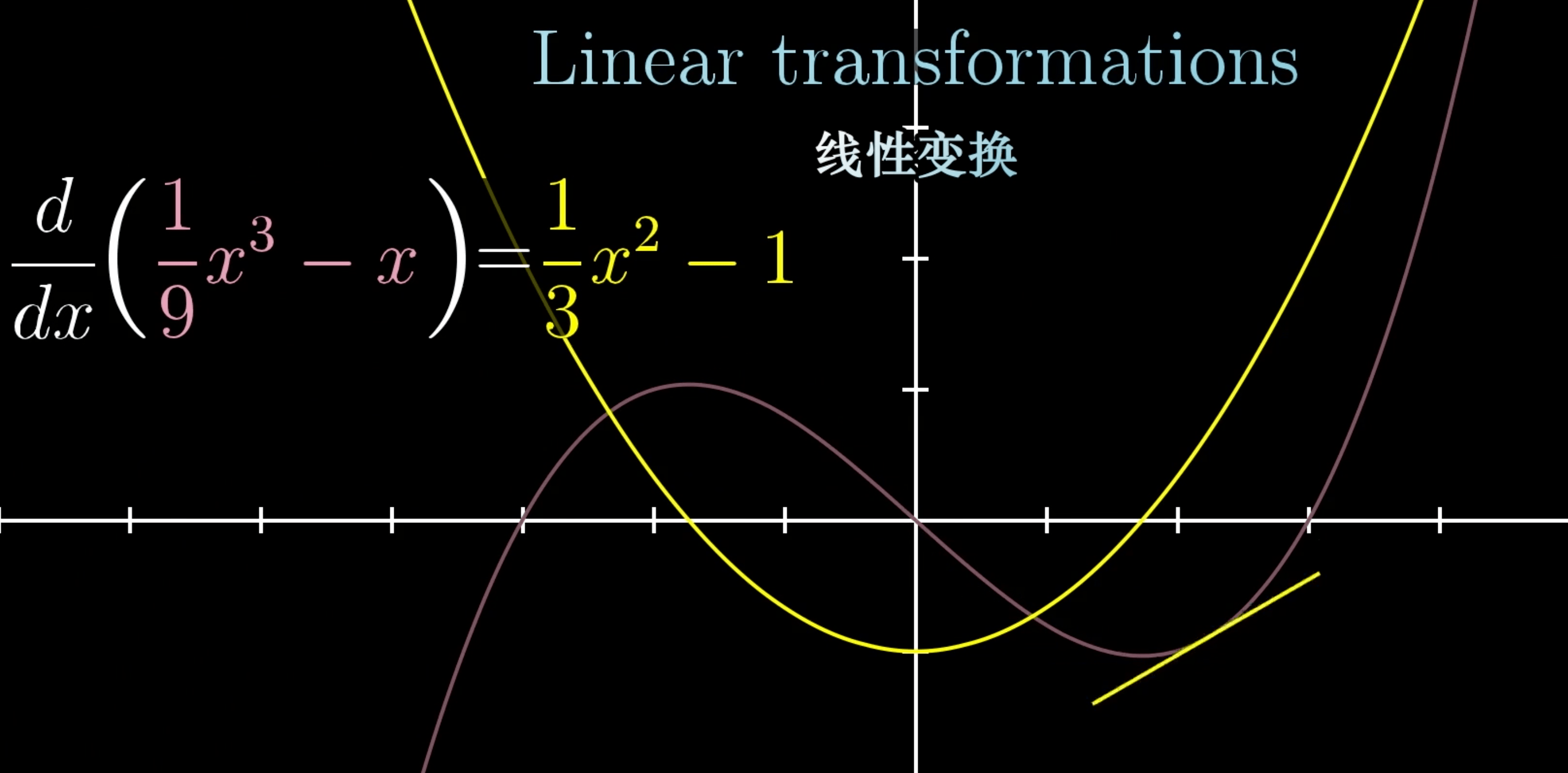
线性
线性变换保持向量 加法 运算和 数乘 运算
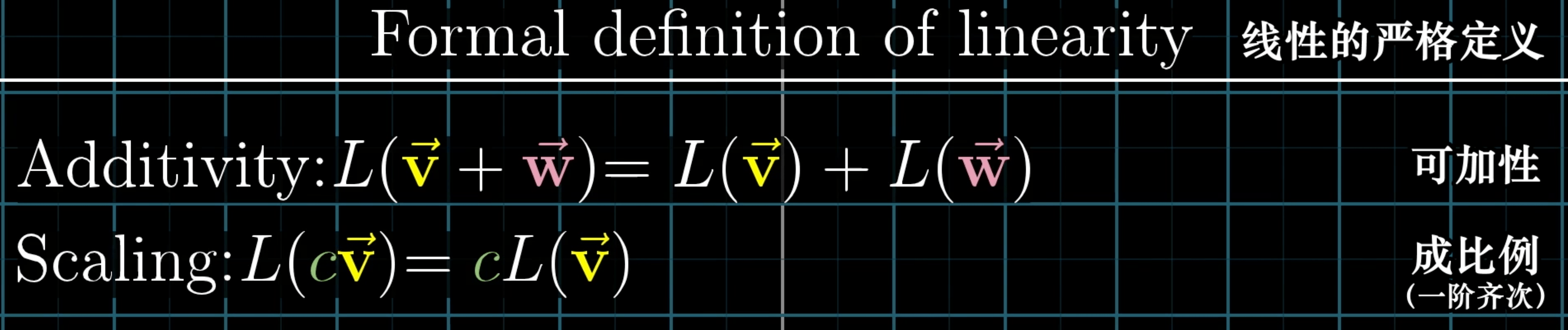
求导是线性的


基函数
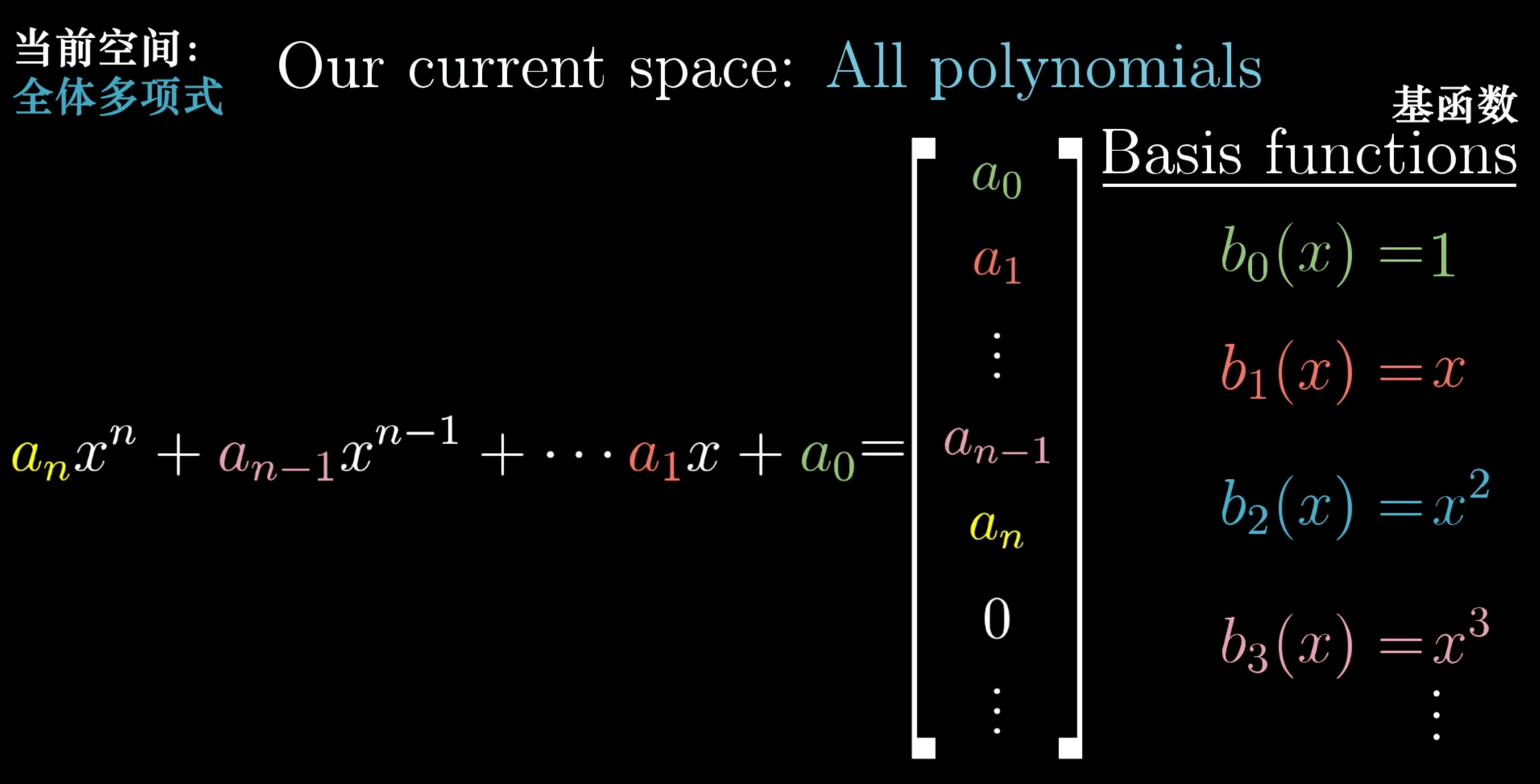
矩阵求导
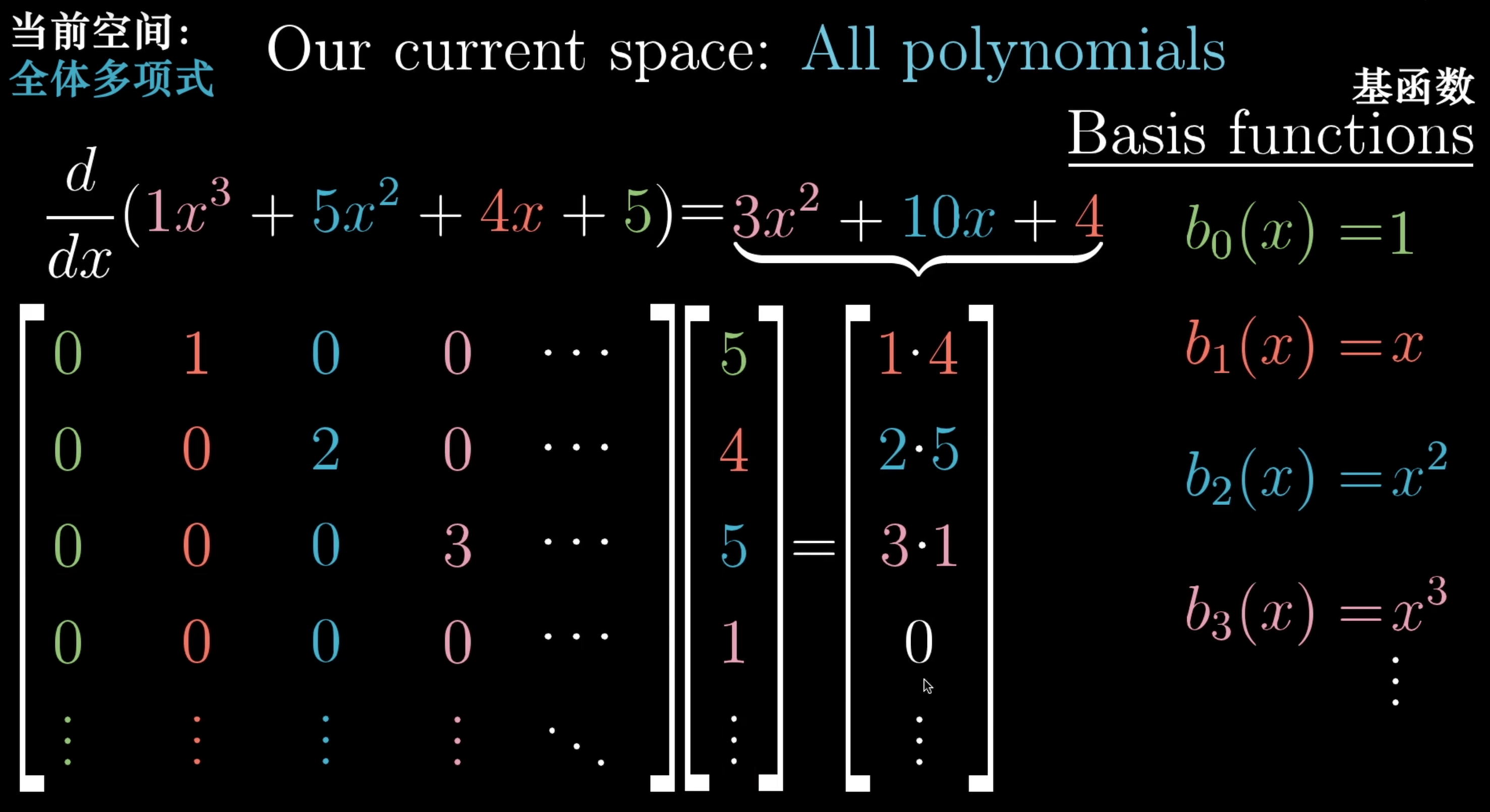
线性代数 vs 函数

向量空间
类似向量的事物
- 箭头 (物理)
- 一组数 (计算机)
- 函数
- ...
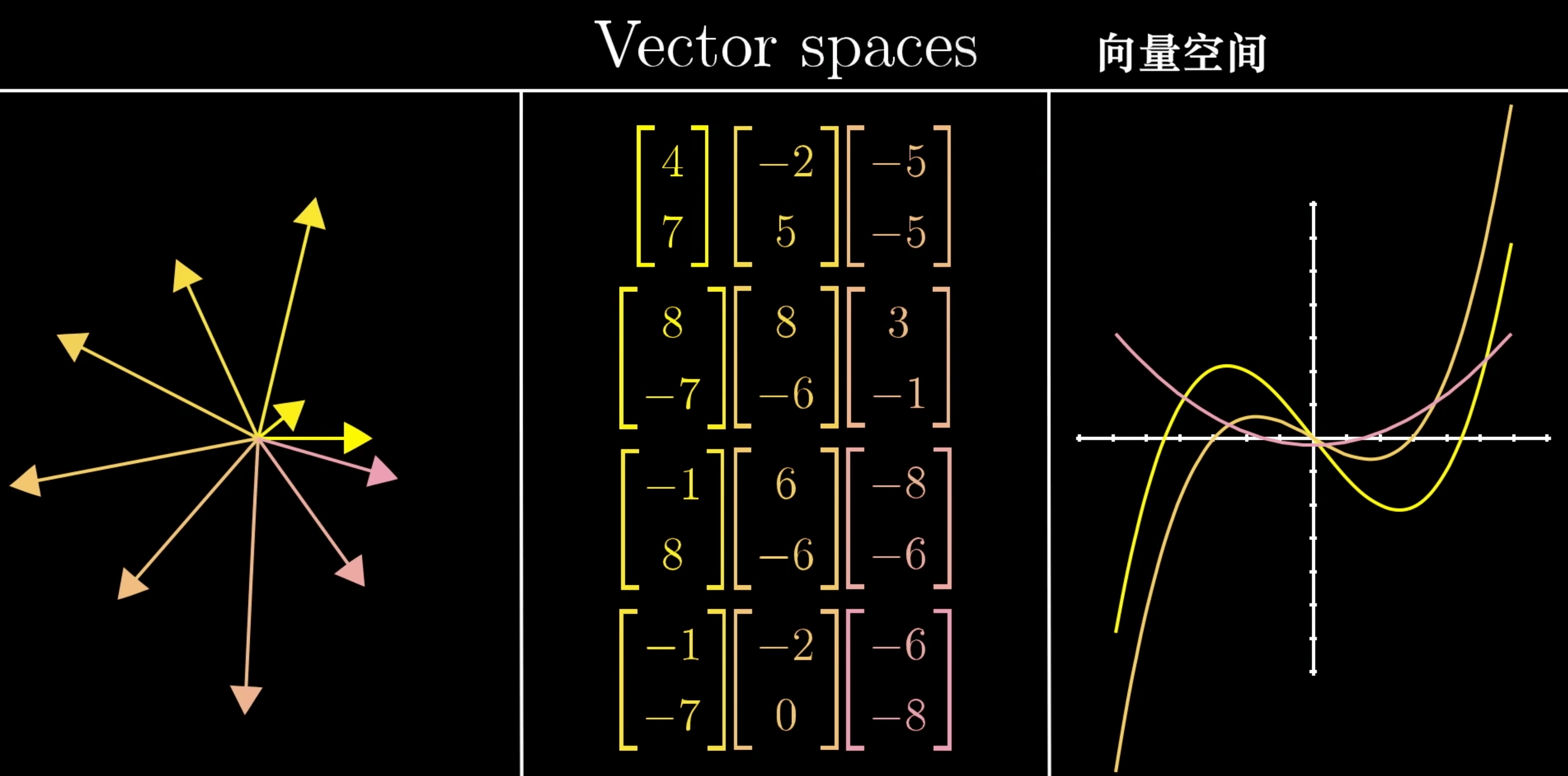
公理

在这里观看完整的“线性代数的本质”播放列表:https://goo.gl/R1kBdb