
书名:极简算法史:从数学到机器的故事
作者:[法]吕克·德·布拉班迪尔
译者:任轶
出版社:人民邮电出版社
出版时间:2018-12
ISBN:9787115500809
一位工程师、一位数学家、一位逻辑学家和一位哲学家一起在苏格兰旅行。他们走在一条路上,栖息在悬岩上的一只黑山羊看着他们路过。
“你们看到了吗?”工程师说,“在苏格兰,山羊都是黑色的!”
数学家反驳道:“可能你想说的是:有些苏格兰山羊是黑色的。”
逻辑学家补充道:“先不要妄下结论。我们只能说:苏格兰至少有一只黑山羊!”
最后,哲学家总结道:“我们唯一能真正确定的是:在这个地方的这只山羊是黑色的!”


















第一部分 莱布尼茨之梦
三次“抽象运动”的硕果
- 算术
- 几何
- 代数
第四次抽象运动
- 逻辑学
- 演绎法
- 这条街上的所有房子都很漂亮。
- 这座房子在这条街上。
- 这座房子很漂亮。
- 归纳法
- 这座房子在这条街上。
- 这座房子很漂亮。
- 在这条街上所有的房子都很漂亮。
- 溯因法
- 这座房子很漂亮。
- 在这条街上所有的房子都很漂亮。
- 这座房子在这条街上。
- 演绎法
数学与语言无关,逻辑却并非如此。
哥德尔证明,罗素是在浪费时间
- 三角形内角和为180°;
- 正方形的内角和为270°。
- 1 是正确的。
- 2 是错误的。
- 在定理中无法对 5 加以证明。
于是有两种可能的情况:
- 要么可以证明 5,但是,由于语句说明的情况与此相反,因而定理不具有逻辑的严密性;
- 要么无法证明 5,因而语句为真,但这意味着,定理不具有完备性。
悖论:“所有克里特人都是骗子”的现代版——
埃庇米尼得斯虽然这么宣布了,但他自己就是克里特人,如果他说的是真的,那么既然他也是克里特人,那说明他也是个骗子,他的话就不可信;而如果他说谎了,那么就印证了“所有克里特人都是骗子”这句话,那说明他所言为真……
第二部分 三座丰碑
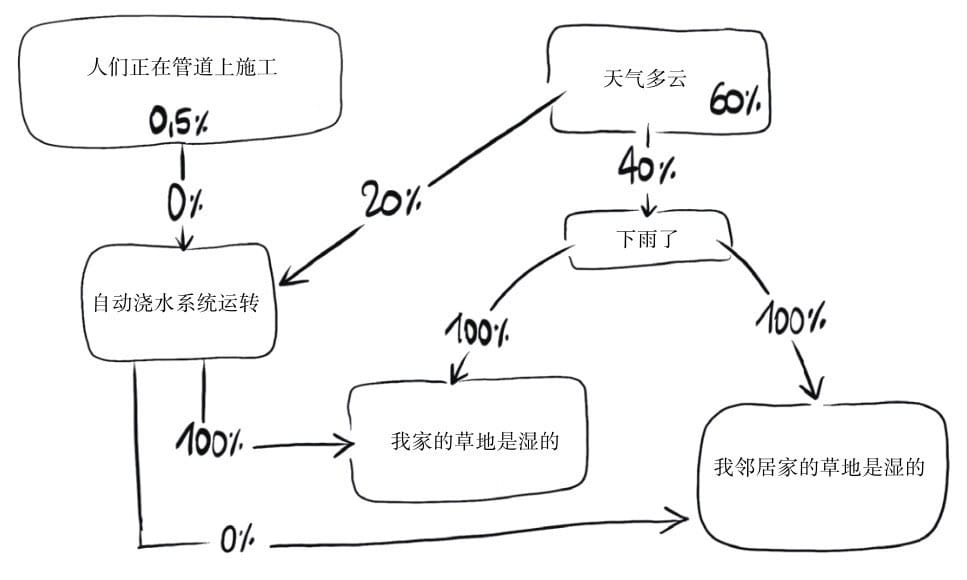
贝叶斯
《关于如何在机会论的框架下解决问题》(Anessay towards solving a problem in thedoctrine of Chance
每个罐子里装有40颗石子。1号罐子里装了30颗白色石子和10颗黑色石子,2号罐子里装有黑白石子各20颗。假设随机拿起一个罐子,并从这个罐子里随机取出一颗石子,且这颗石子是白色的,那么这颗白色石子来自1号罐子的概率是多少?
- 已知被选中的石子是白色的,用获得白色石子的概率乘以选择1号罐子的概率;
- 已知白色石子来自1号罐子,用选择1号罐子的概率乘以获得白色石子的概率。
A:1号罐子的假设
B:白色石子的假设
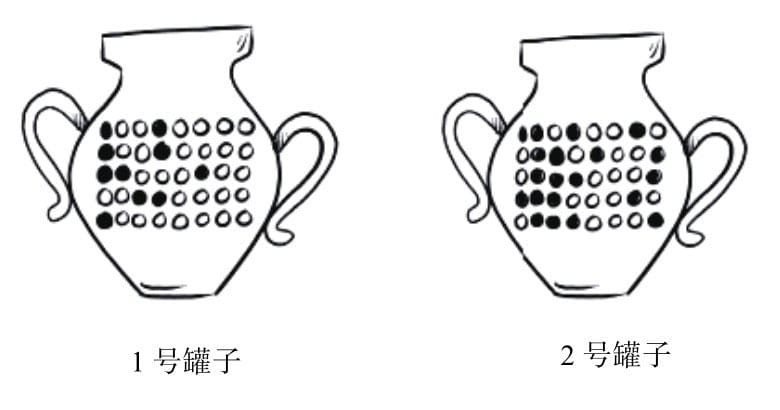
\[ p(\mathrm{B}). p(\mathrm{A} / 已知 \mathrm{B})=p(\mathrm{A}). p(\mathrm{B} / 已知 \mathrm{A}) \]
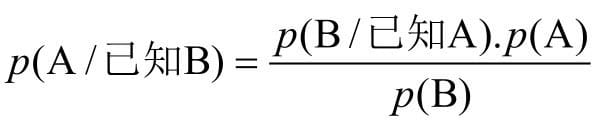
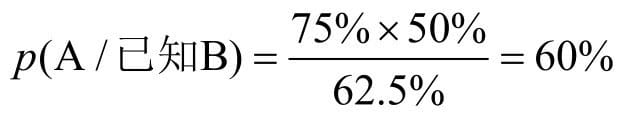
香农证明,如何计算1+1
信息动力学,两个定理分别探讨的是 信息量 和信息的 质量。
- 第一个定理涉及信息的压缩
- 编码一条信息所需的最少符号数量是多少?
- 第二个定理涉及信息的传输
- 为了在终点处获取从起点处发出的准确信息,需要哪些必要条件?
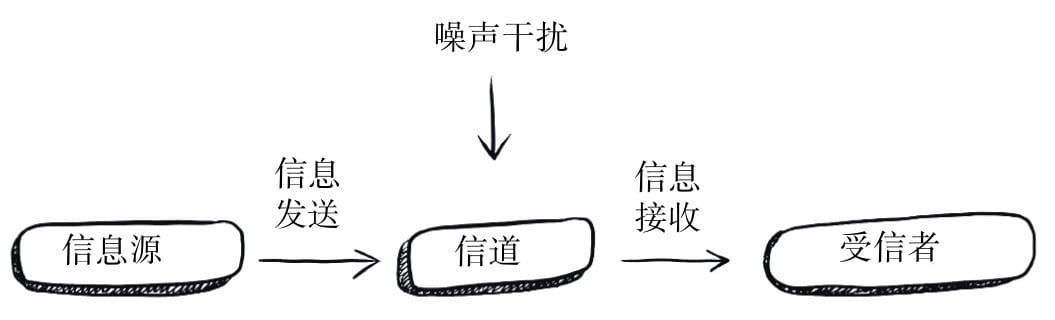
测量单位。就像卡路里可以量化热交换一样,香农提出的“比特”(bit,也叫位)的概念用于测量信息量。
比特是一个二进制数字,可以取0或1的值。
信息的测量应该满足一个苛刻的关系
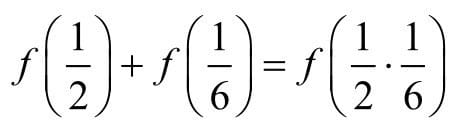
其中,\(f\) 只能是对数函数,因为根据定义,同一底数的两个正数的对数之和等于这两个数的积的对数。
香农的公式能让我们借助经验计算出摩尔斯电码的效率为85%!我们不得不佩服公式发明者出色的直觉。

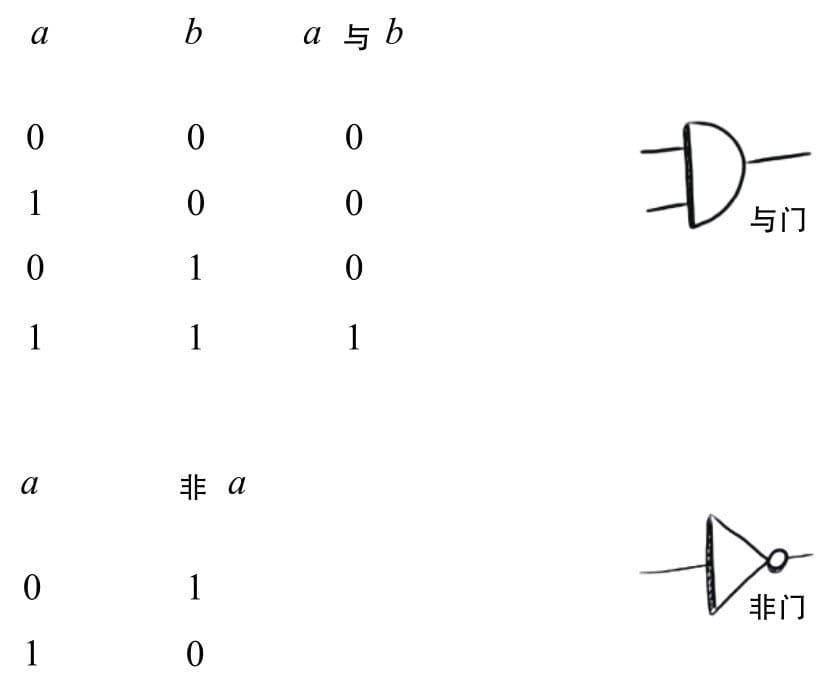
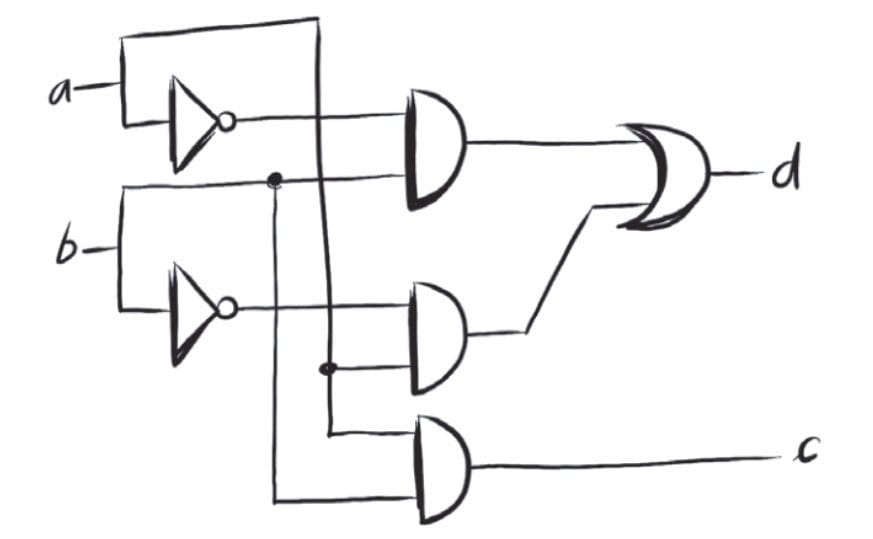
香农数:国际象棋棋局的理论数目,结果是 \(10^{120}\)
诺伯特·维纳与控制论(cybernetics)
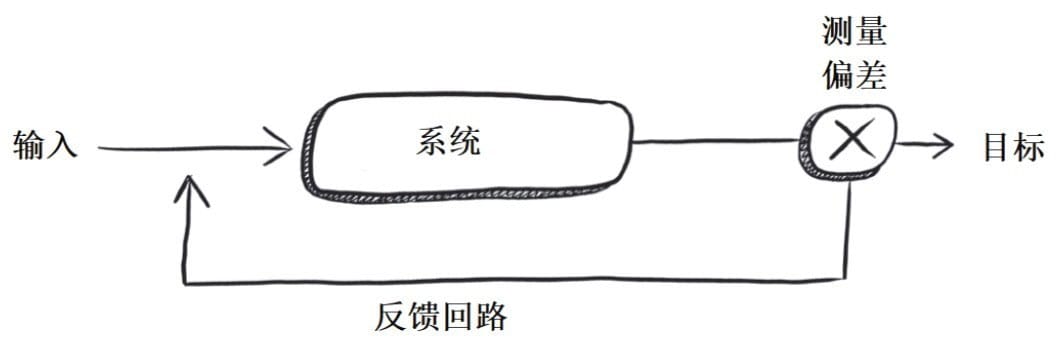
第三部分 自动化理性批判
科学是父亲教给儿子。
技术是儿子教给父亲。
——米歇尔·塞尔
算法(algorithm)
三种不确定性
- 圣诞节是在什么时候?你不知道,我也不知道。
- 谁将在2022年当选法国总统?你不知道,我也不知道。
- 因为我们甚至不知道“我们不知道”。
第三类不确定性涉及了“没人提出的问题”。在这种情况下,超级计算机也没有用了……因为没有什么可以计算的!
这类事件通常被称为 “黑天鹅”。
这一说法是用来纪念一位18世纪的英国探险家,这位探险家曾确信所有天鹅都是白色的,然而,他在澳大利亚逗留期间,惊讶地看到了一只黑天鹅——没有一个欧洲人曾对这类水禽的颜色提出过疑问。于是,黑天鹅成为第三类不确定性的象征。
全球化管理的重要性
- 互联网并非公共空间。
- 互联网并非全球性的。
- 互联网并非环保。
- 互联网既不是虚拟的,也不是非物质的。
- 互联网并非透明。(大数据)
- 互联网并非中立。(算法)
- 互联网在其运作过程中并没有完全被理解。
- 互联网并非市场经济的保障。
- 互联网并非民主的保障。
- 互联网并非掌握真相。
- 互联网积累的信息正在变得无用。
- 互联网并非友善。(暴力)
- 互联网是脆弱的。(Bug)
- 互联网并非自动。(参数)
- 互联网并非自由。(surf,原意是冲浪)
- 互联网只有部分是可访问的。(暗网)
- 互联网并非优质教育的保障。
- 互联网并非公平。
- 互联网并非免费。
- 互联网是我们的工具,而我们也是互联网的工具。(测试)
- 互联网不好也不坏。
- 互联网,尤其对民主国家来说,是空前的挑战。
死亡电脑社
互联网上的预言大师名为 奇点。
奇点指的是机器与人类彻底融合的时刻,这种情况注定会在某一天发生。
人工智能:许多问题之一
智商(IQ)
- 音乐智力,这种智力体现为对声音和节奏的感知度。它寻找音符的含义,并想象改编为其他乐曲的可能性。
- 运动智力,这种智力能释放身体各个部位的潜能。它组织了用来解决特定问题的最佳动作序列。
- 人际关系智力(或情感智力),这种智力能识别他人的感受和意图。它能感知到对于谈判、合作和互动等行为来说,什么是重要的因素。
- 视觉智力,这种智力可以从三个维度进行思考。它能让我们在建模之前、在空间内移动物体之前、在看到被要求思考的东西之前,就先进行想象。
- 语言智力,这种智力是利用语言反应的能力。如果有必要,这种智力甚至能够催生新的语言。
答案
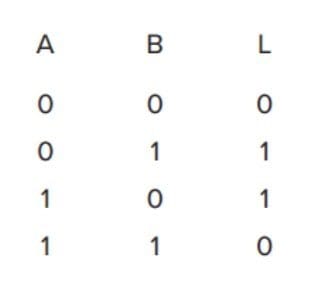
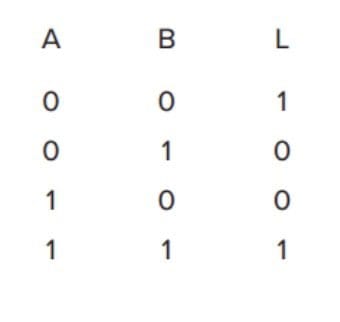
从古希腊哲学到数学,从逻辑推理到“无所不能”的计算机。柏拉图、莱布尼茨、罗素、香农、图灵……一个个伟大的思想家试图从数学公式中证明推理的合理性。
他们是凭借天赋制胜,还是在鲁莽地大胆一搏?
如何将逻辑赋予数学意义?
如何从简单运算,走向复杂智慧?
一场人类探索数学、算法与逻辑思维,并最终走向人工智能的梦想之旅,展现了哲学家、逻辑学家与数学家独特的思维方式,探讨了算法与人工智能对科学和社会的巨大影响。