数学它其实是一种思维模式,考验的是一个 人归纳、总结和抽象的能力
——《程序员的数学基础课》1。
如何学习新技术
- 第一阶段:怎么使用
- 第二阶段:如何实现,原理是什么
- 第三阶段:为什么这样实现
- 明确需求
- 用多少学多少
- 理解数学的本质
- 数学思想与数学逻辑
基础思想
二进制

余数
余数总是在一个固定的范围内。
同余定理用来 分类/均分 的。

迭代法
不断地用旧的变量值,递推计算新的变量值。
- 求数值的精确或者近似解
- 二分法(Bisection method)
- 牛顿迭代法 (Newton’s method)
- 在一定范围内查找目标值
- 二分查找
- 机器学习算法中的迭代
- K- 均值算法(K-means clustering)
- PageRank 的马尔科夫链(Markov chain)
- 梯度下降法(Gradient descent)
很多时候机器学习 的过程,就是根据已知的数据和一定的假设,求一个局部最优解

数学归纳法
数学归纳法的一般步骤是这样的:
- 证明基本情况(通常是 \(n = 1\) 的时候)是否成立;
- 假设 \(n = k-1\) 成立,再证明 \(n=k\) 也是成立的( \(k\) 为任意大于 \(1\) 的自然数)。
和使用迭代法的计算相比,数学归纳法 最大的特点就在于“归纳”二字。它已经总结出了规律。只要我们能够证明这个规律是正 确的,就没有必要进行逐步的推算,可以节省很多时间和资源。
递归调用的代码和数学归纳法的逻辑是一致的。

递归
- 初始状态,也就是 \(n=1\) 的时候,命题是否成立;
- 如果 \(n=k-1\) 的时候,命题成立。那么只要证明 \(n=k\) 的时候,命题也成立。其中 \(k\) 为大于 \(1\) 的自然数。

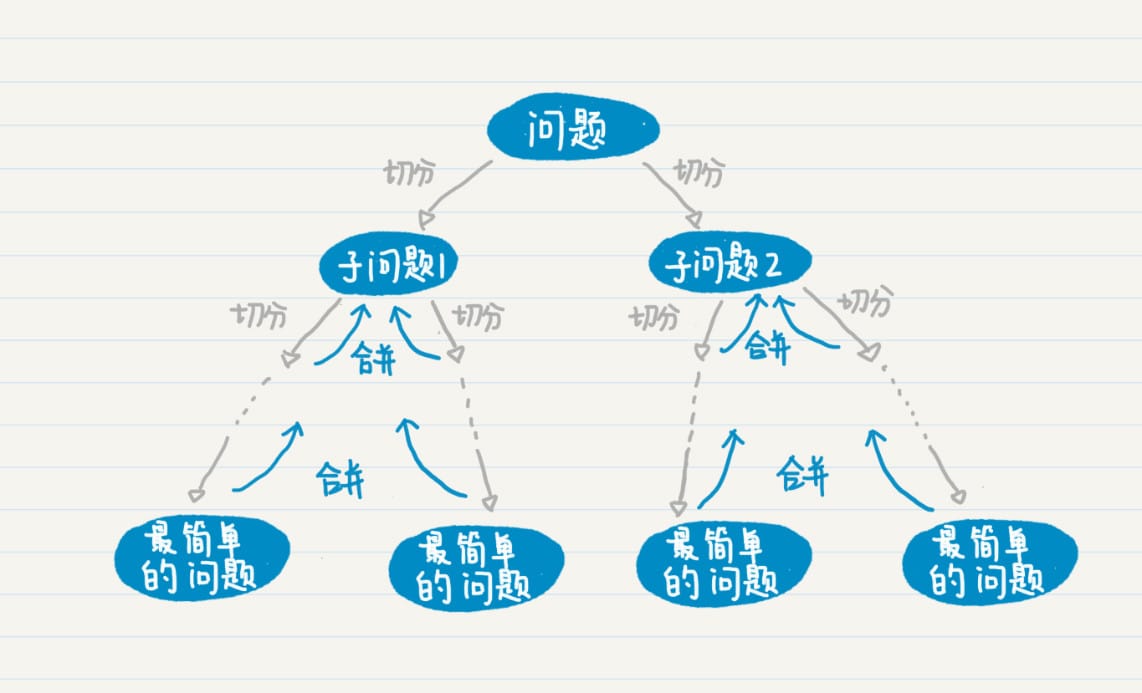
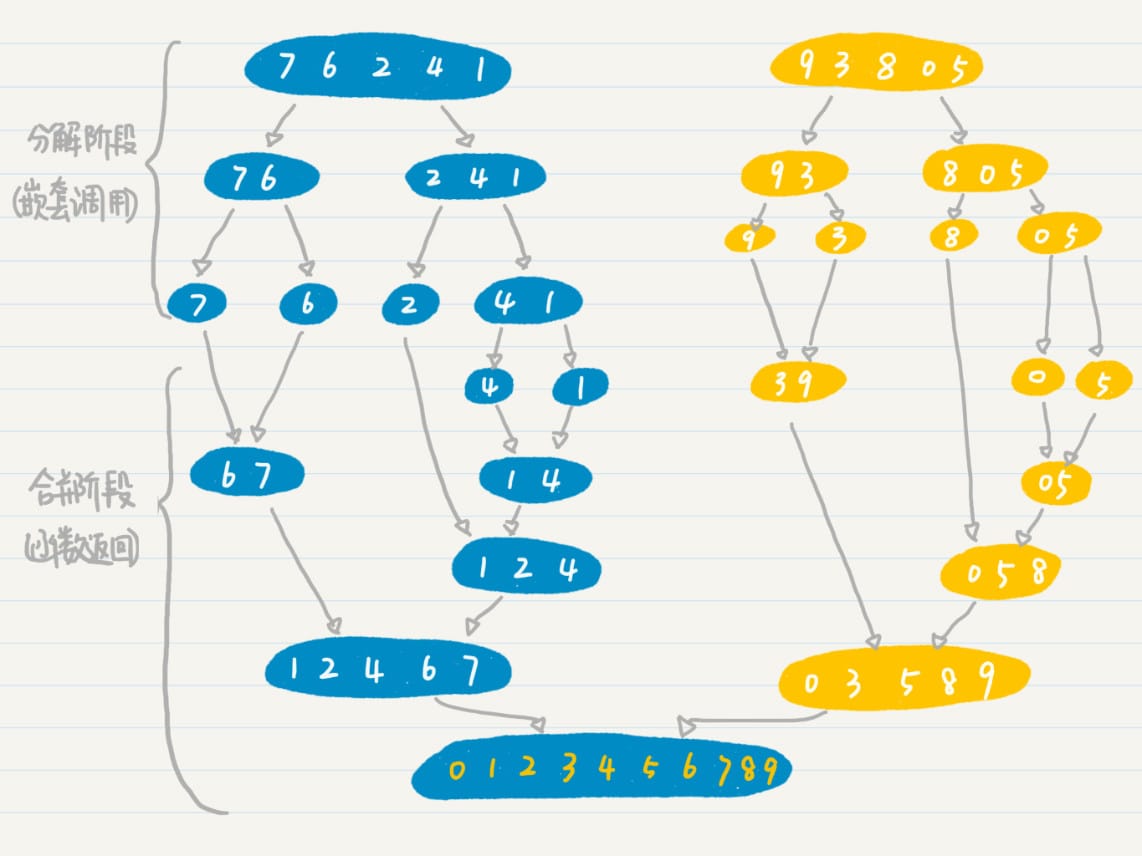
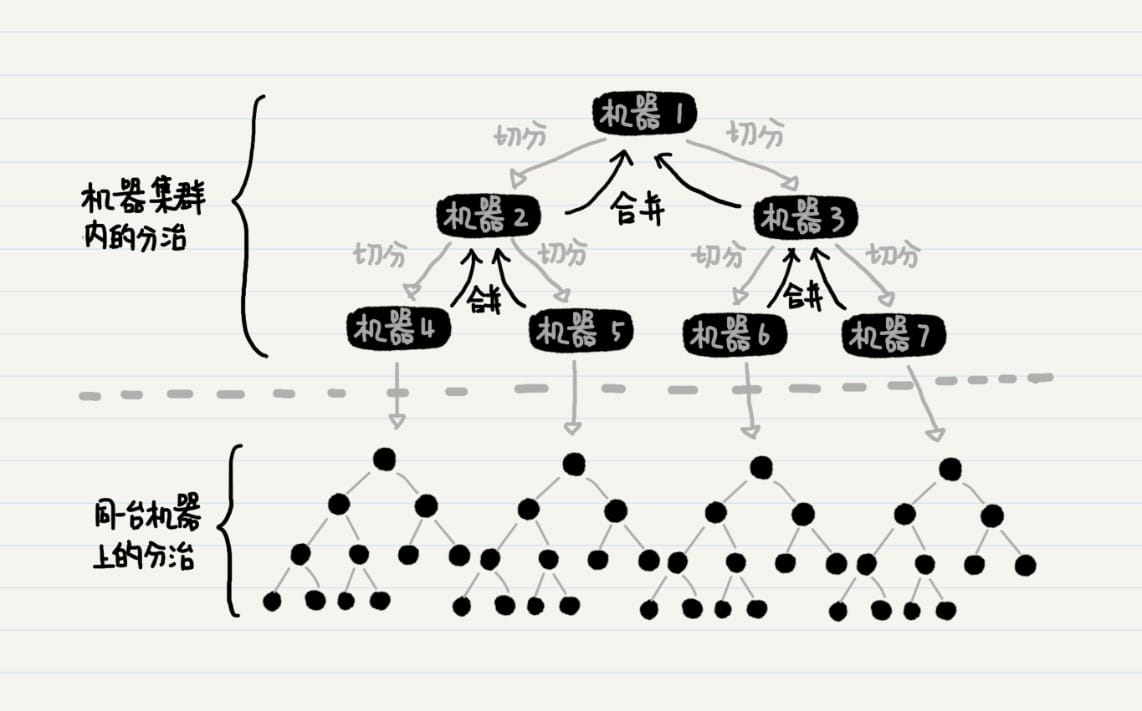

排列
排列,一般地,从 \(n\) 个不同元素中取出 \(m(m≤n)\) 个元素,按照一定的顺序排成一列,叫做从 \(n\) 个元素中取出 \(m\) 个元素的一个排列(permutation)。特别地,当 \(m=n\) 时,这个排列被称作全排列(all permutation)。

组合

动态规划


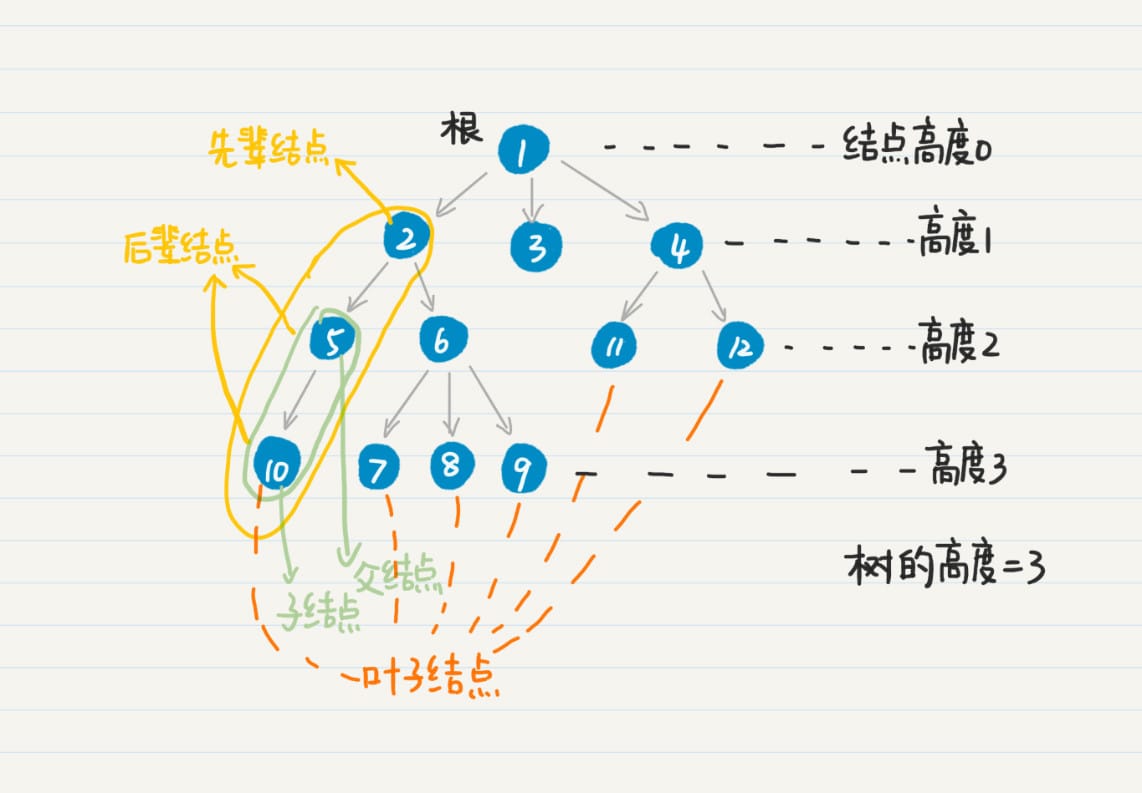
树的深度优先搜索
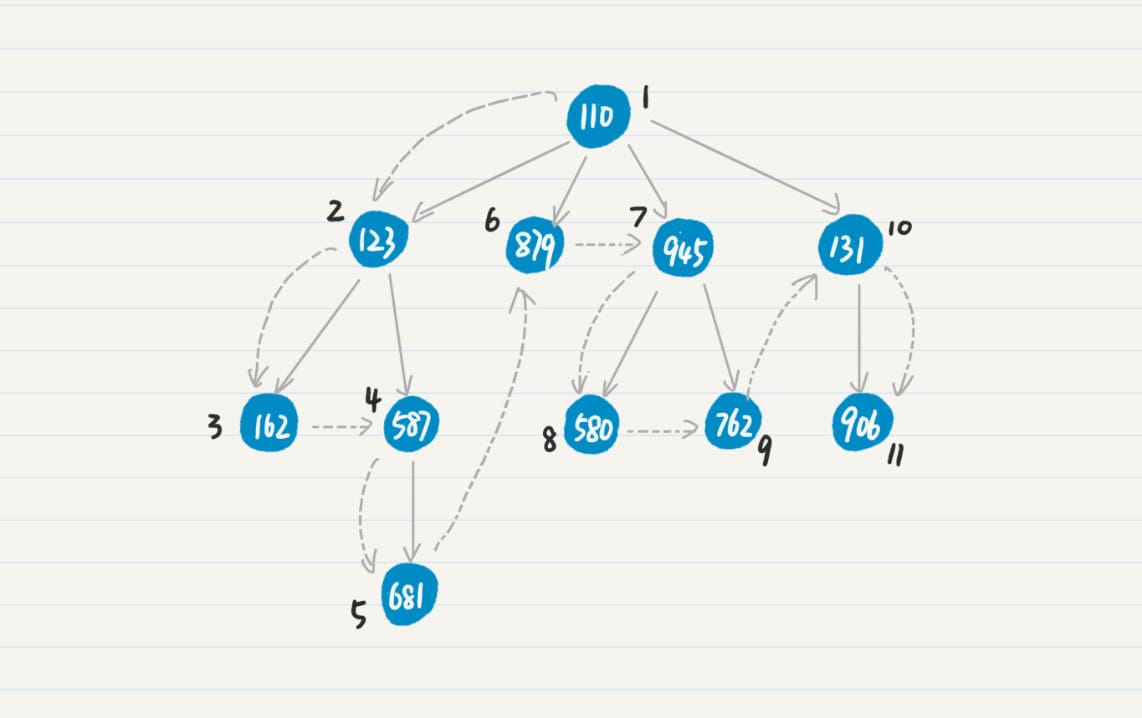


树的广度优先搜索
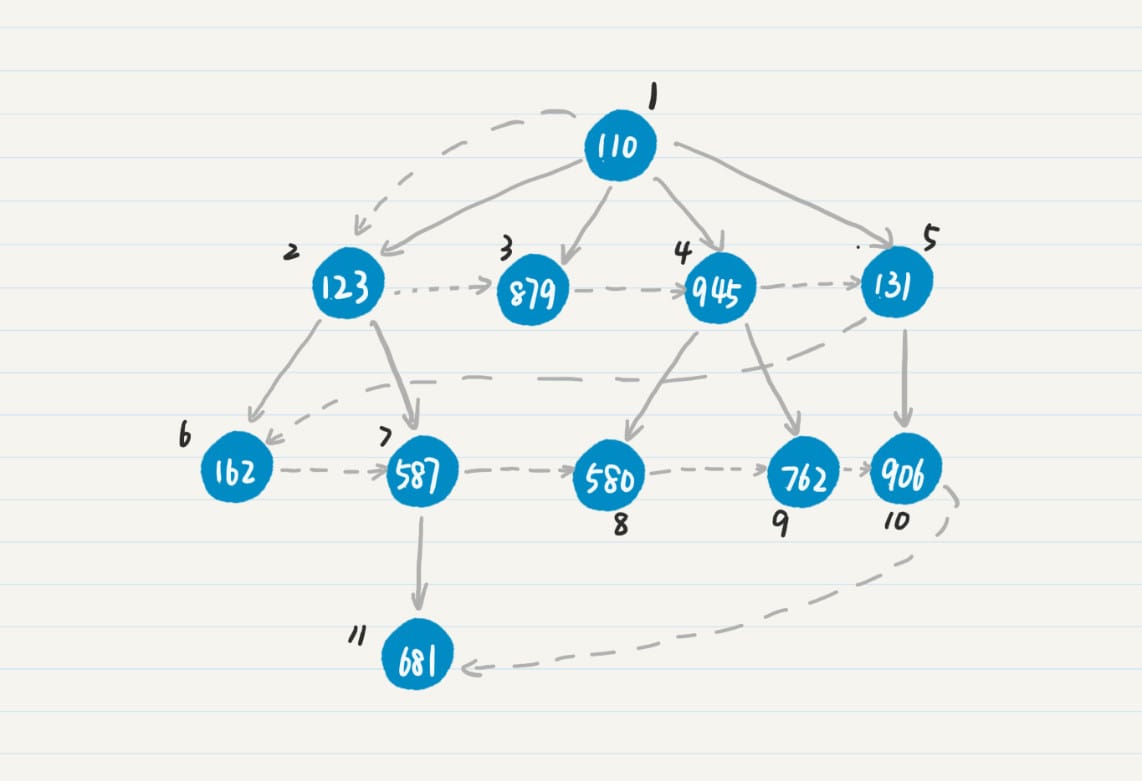


从树到图
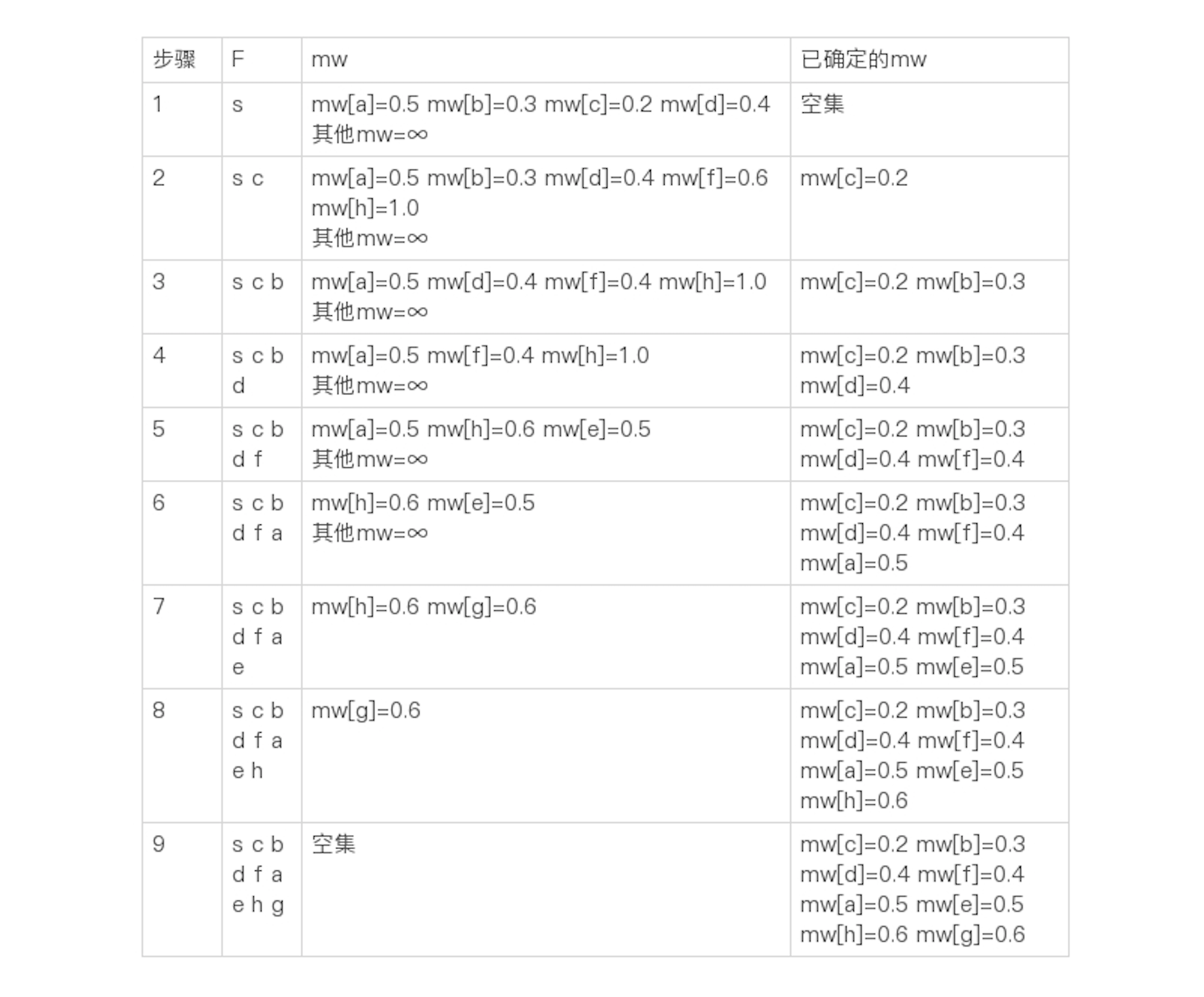

时间和空间复杂度

概率统计
概率和统计
概率(Probability)
- 随机变量(Random Variable):事件所有可能出现的状态
- 概率分布 (Probability Distribution):每个状态出现的可能性
- 离散 型随机变量(Discrete Random Variable)
- 连续型随机变量(Continuous Random Variable)
对于离散型随机变量,通过联合概率 \(P(x, y)\) 在 \(y\) 上求和,就可以得到 \(P(x)\),这个 \(P(x)\) 就 是边缘概率(Marginal Probability)
概率论研究的就是这些概率之间相互转化的关系,比如联合概率、条件概率和边缘概率。
- 决策树(Decision Tree)
- 信息熵(Entropy)/ 香农熵(Shannon Entropy)
- 信息增益(Information Gain)
- 基尼指数(Gini)
概率和统计 互逆
- 概率论是对数据产生的过程进行建模,然后研究某种模型所产生的数据有什么特性。
- 通过已知的数据,来推导产生这些数据的模型是怎样的。
概率基础
概率分布描述的其实就是随机变量的概率规律
参考:看见统计2
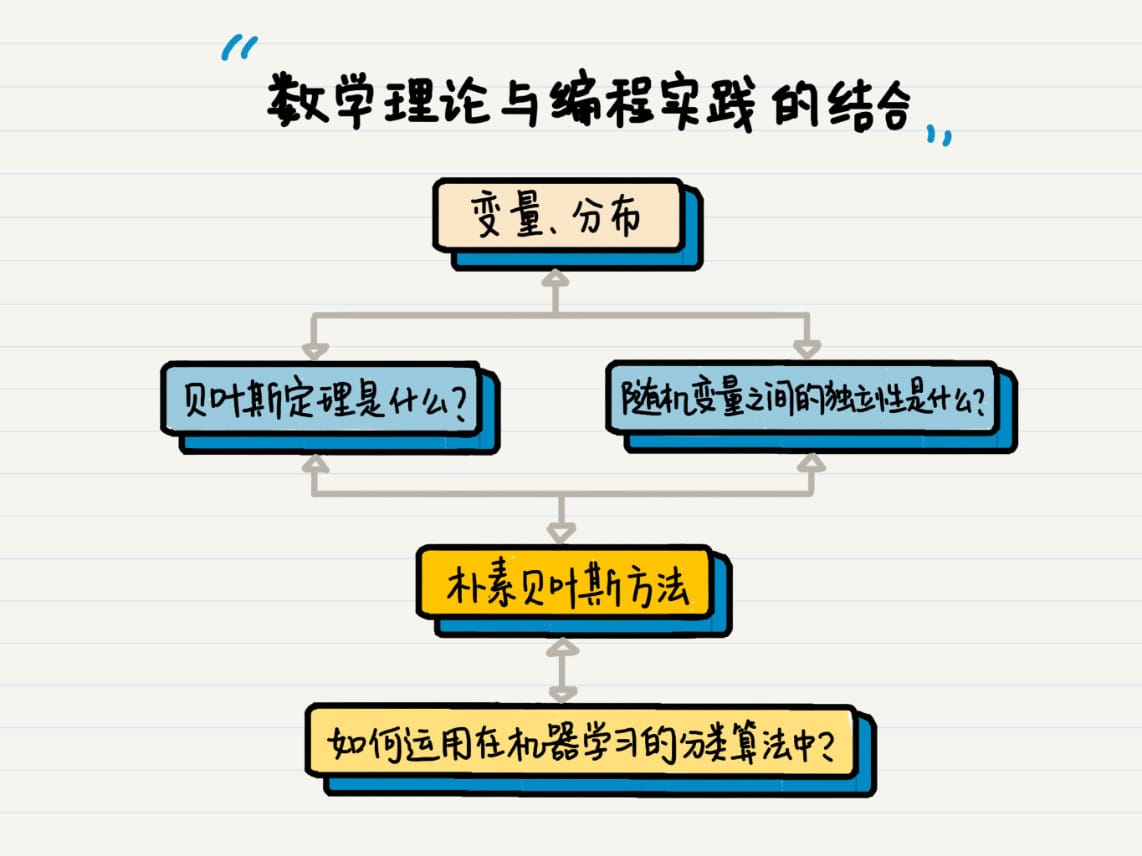
朴素贝叶斯

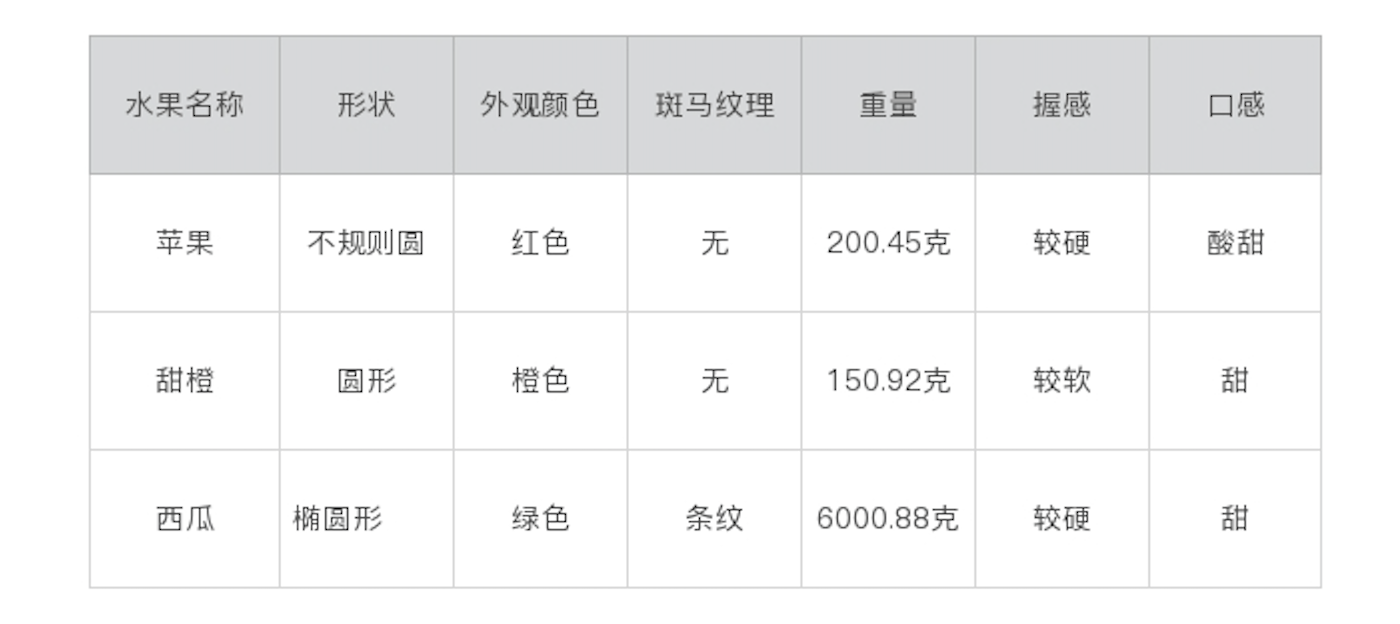
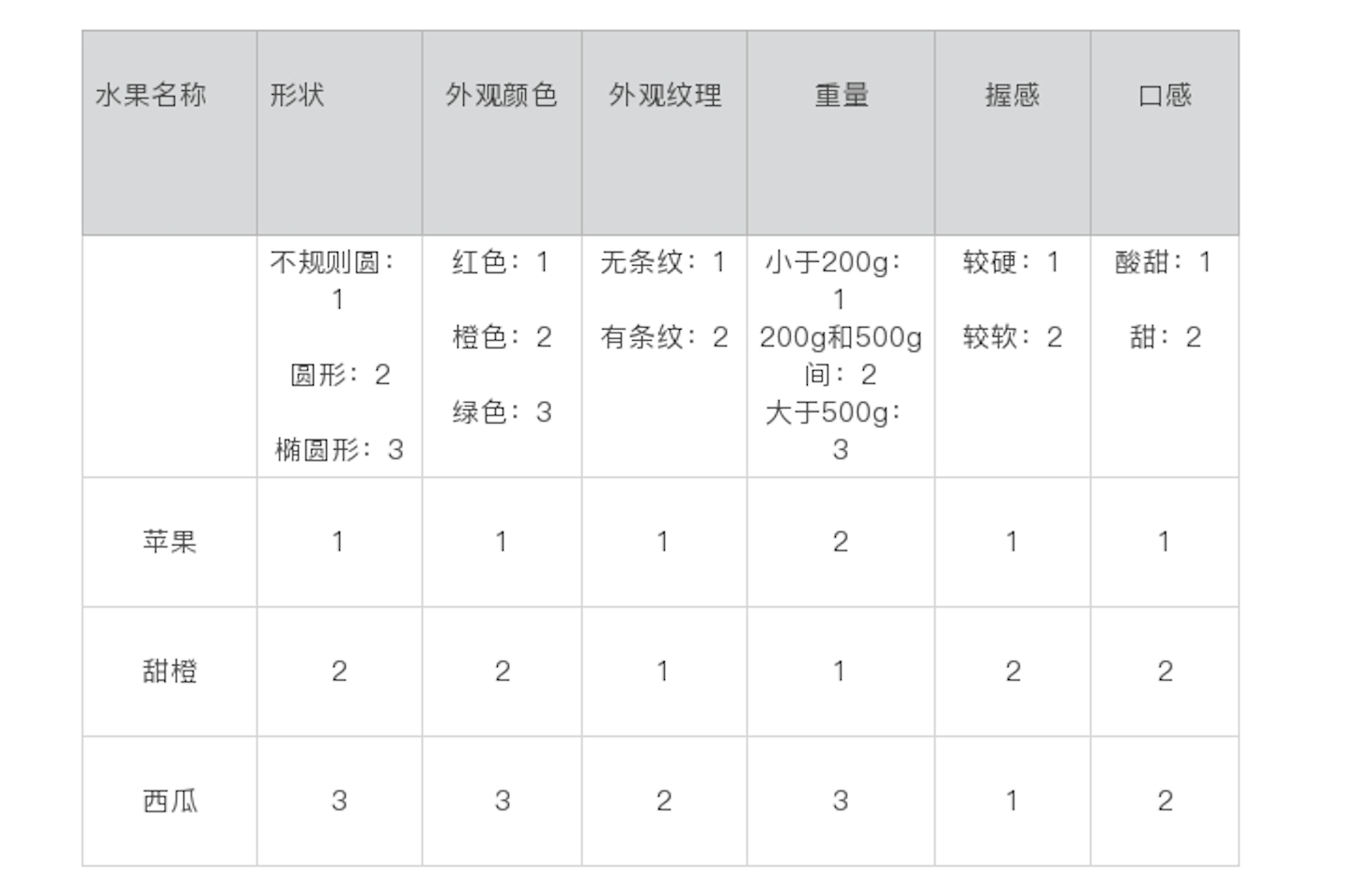
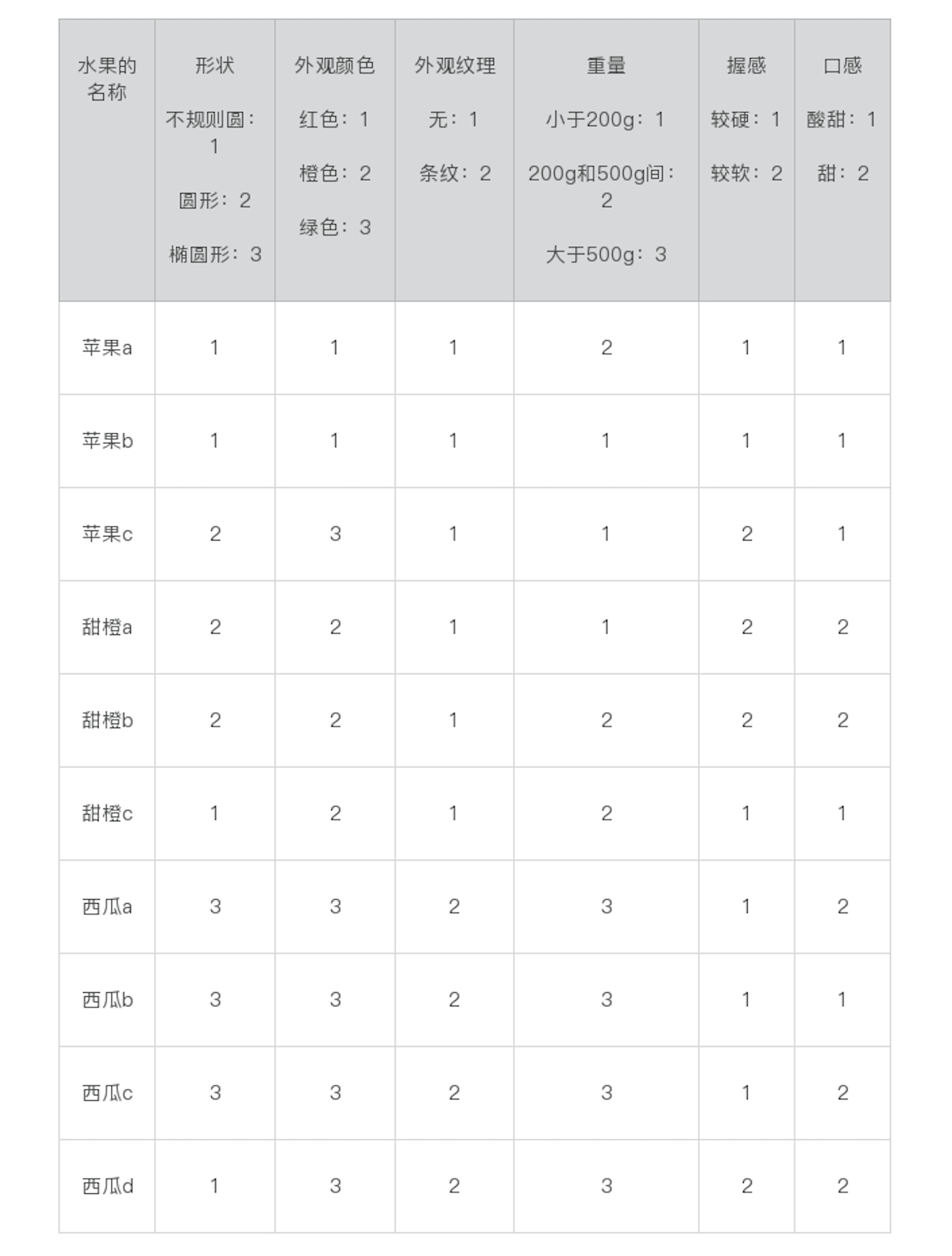
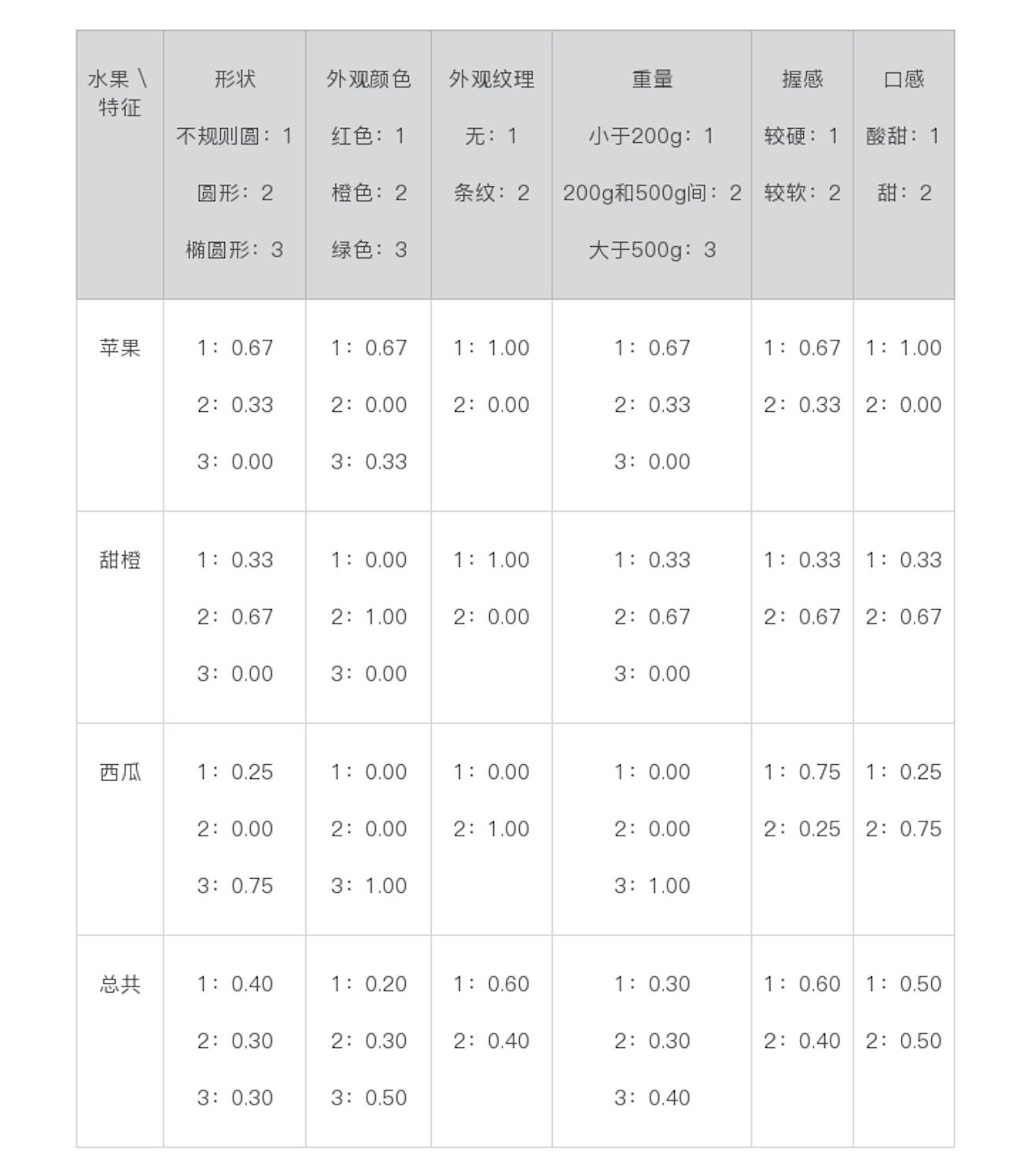
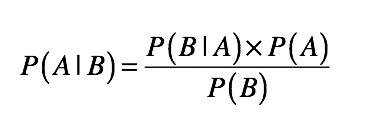

文本分类
文本分类系统的基本框架
- 采集训练样本
- 预处理自然语言
- 训练模型
- 实时分类预测

基于自然语言的预处理
- 分词
- 基于字符串匹配
- 基于统计和机器学习
- 隐马尔科夫模 型(HMM,Hidden Markov Model)
- 条件随机场(CRF,Conditional Random Field)
- 取词干和归一化
- 停用词
- 同义词和扩展词
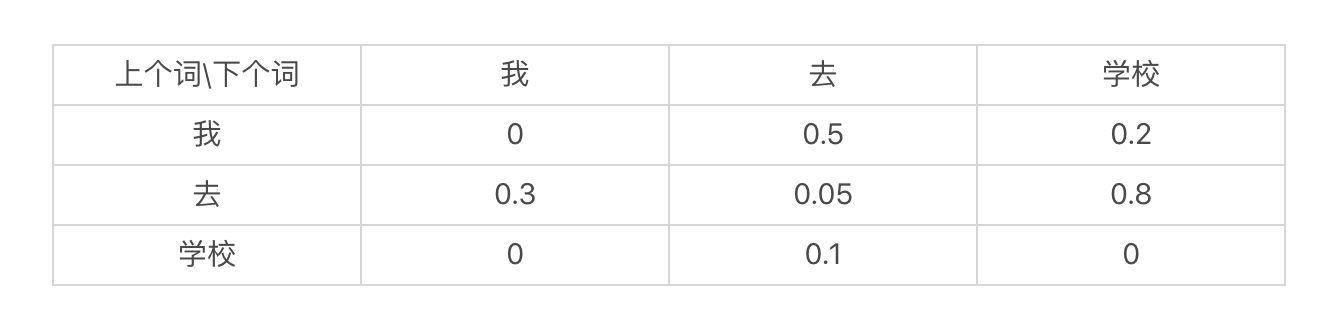
语言模型
语言模型是什么?
- 链式法则
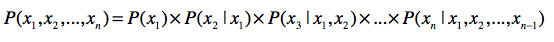
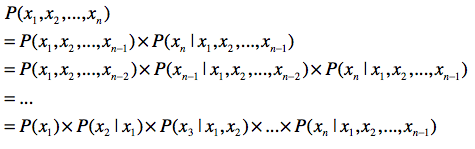
- 马尔科夫假设
理解了链式法则,我们再来看看马尔可夫假设。
这个假设的内容是:
任何一个词 \(w_{i}\) 出现的概率只和它前面的 \(1\) 个或若干个词有关。
基于这个假设,我们可以提出 多元文法 (Ngram)模型。Ngram 中的“N”很重要,它表示任何一个词出现的概率,只和它前 面的 \(N-1\) 个词有关。
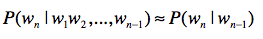
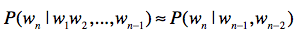
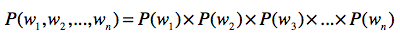
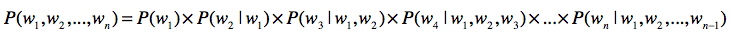
语言模型的应用
- 信息检索
- 中文分词
第一,使用联合概率,条件概率和边缘概率的“三角”关系,进行相互推导。链式法则就 是很好的体现。
第二,使用马尔科夫假设,把受较多随机变量影响的条件概率,简化为受较少随机变量影 响的条件概率,甚至是边缘概率。
第三,使用贝叶斯定理,通过先验概率推导后验概率。在信息检索中,给定查询的情况下 推导文档的概率,就需要用到这个定理。
马尔科夫模型
假设:每个词出现的概率和 之前的一个或若干个词有关。
如果把词抽象为一个状态,那么我们就可以认为,状态到状态之间是有关联的。前一个状 态有一定的概率可以转移到到下一个状态。如果多个状态之间的随机转移满足马尔科夫假 设,那么这类随机过程就是一个马尔科夫随机过程。而刻画这类随机过程的统计模型,就是 马尔科夫模型(Markov Model)。
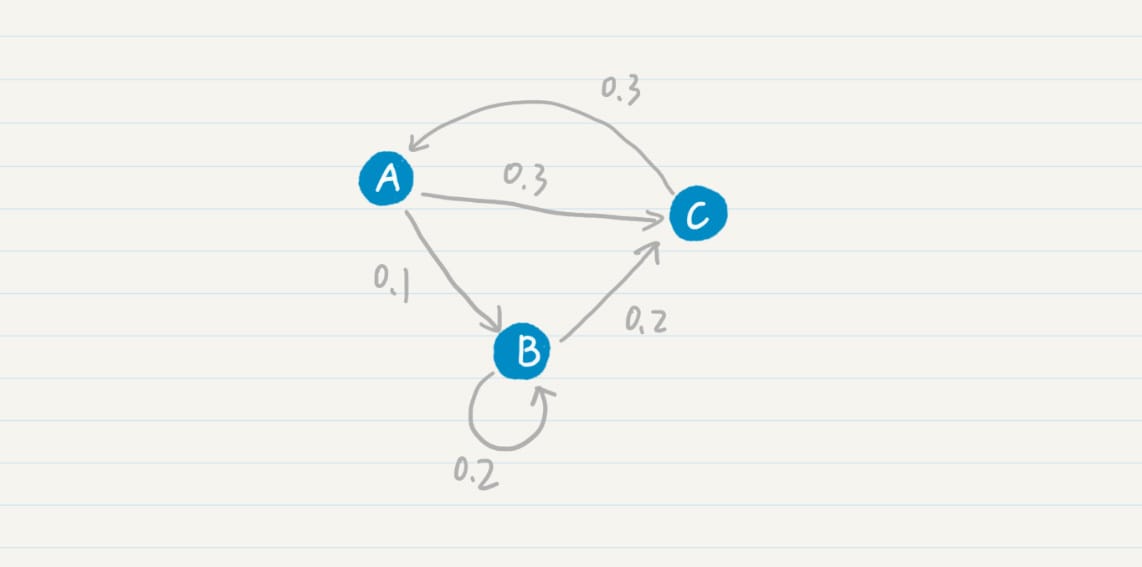
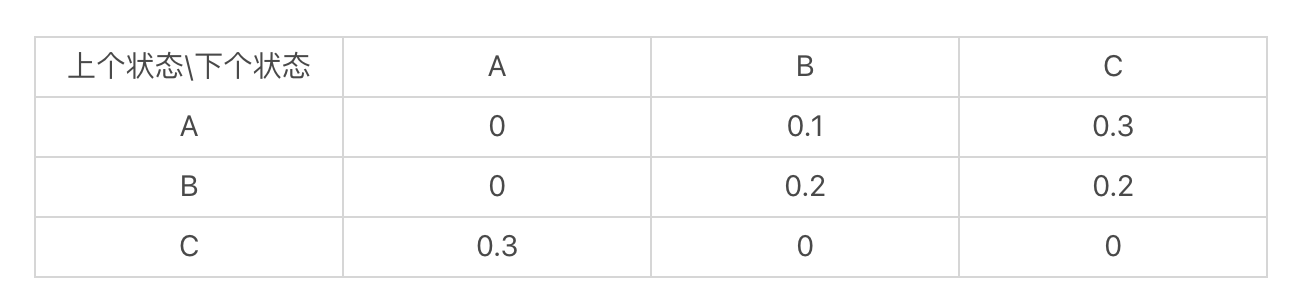
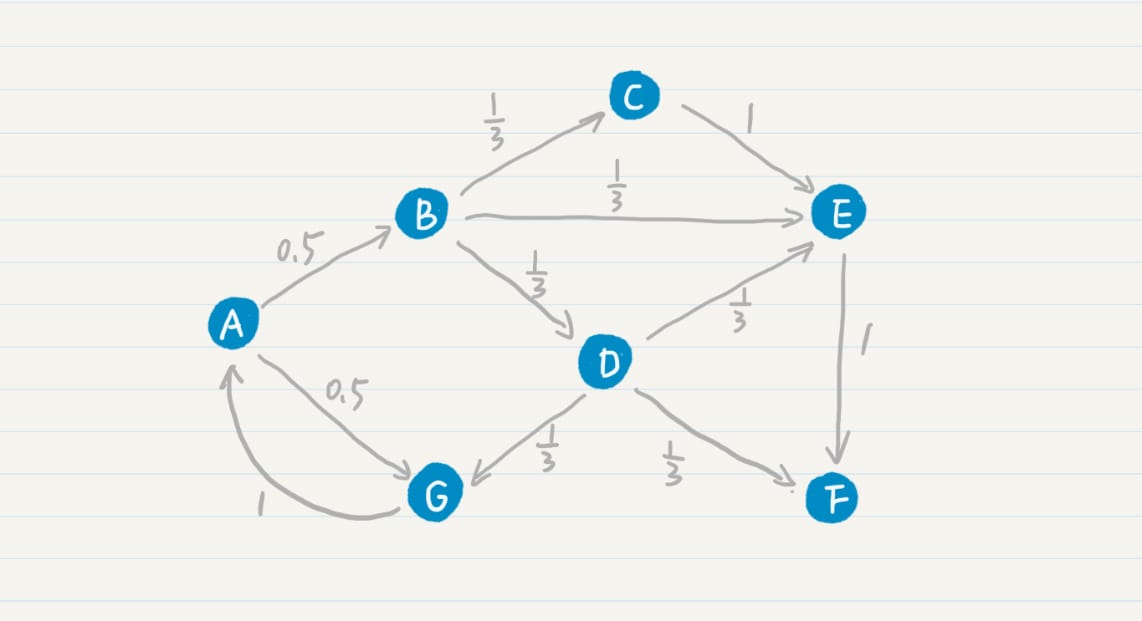
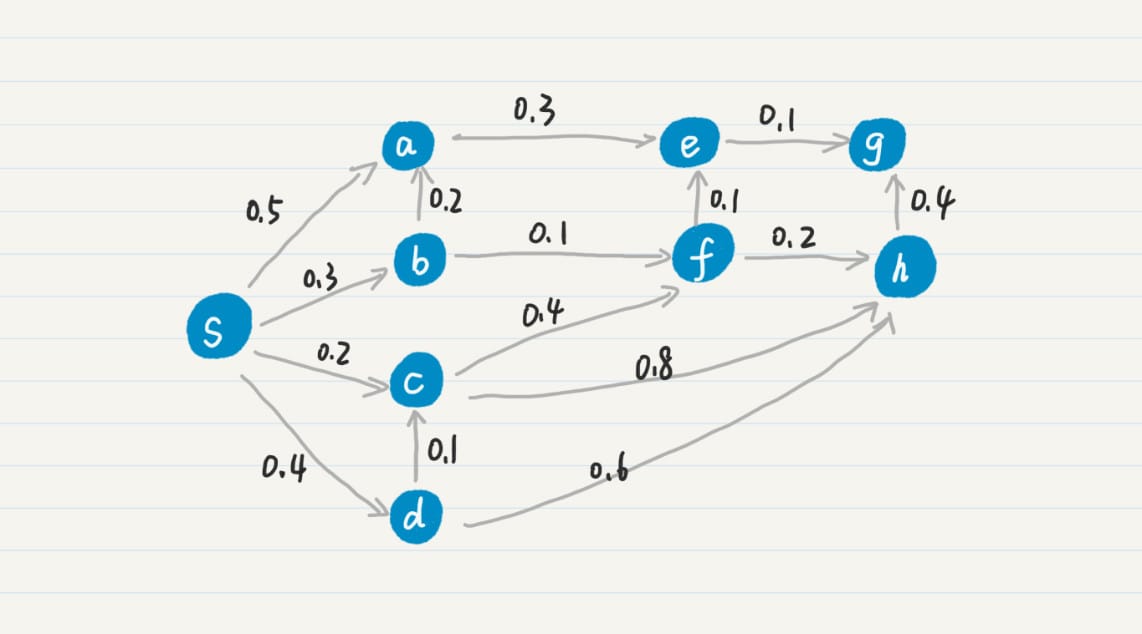
PageRank 公式
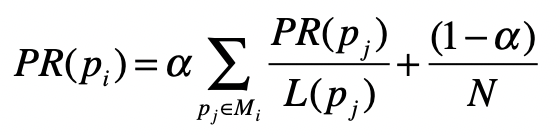
隐马尔科夫模型
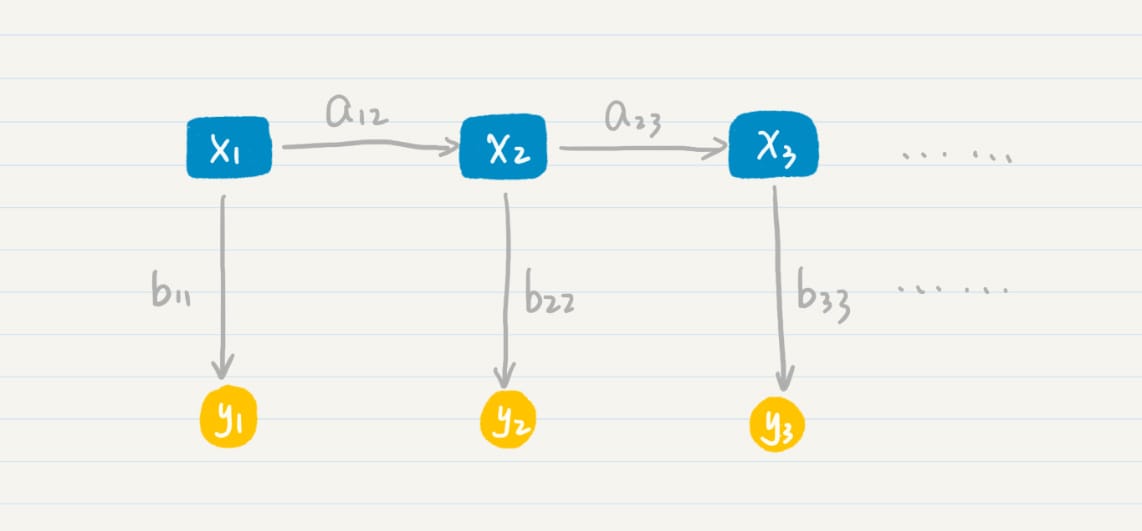
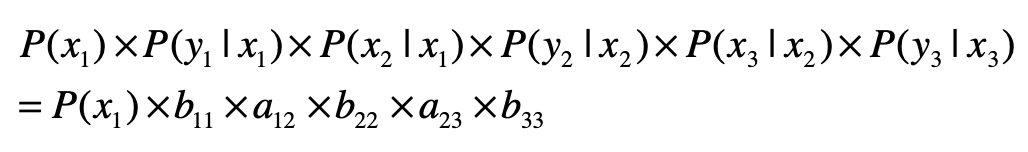
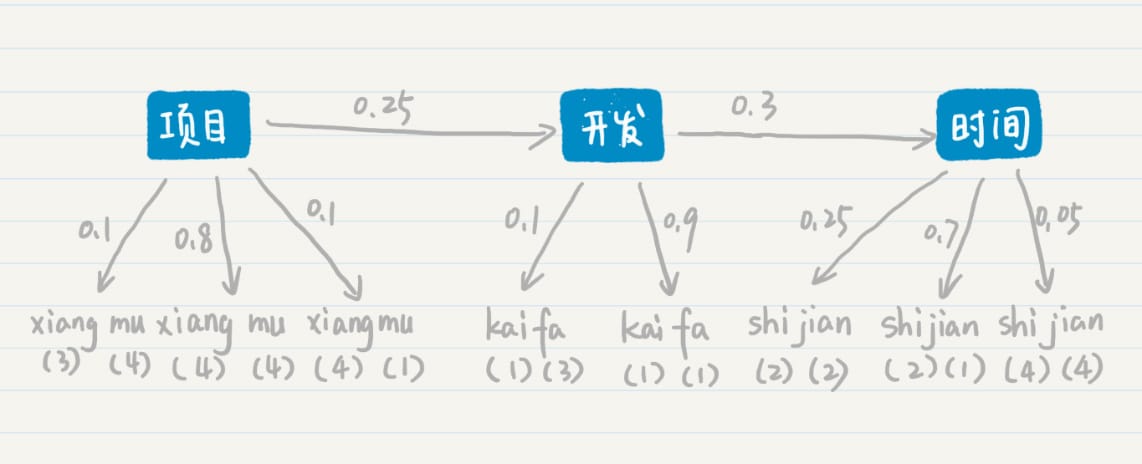
信息熵

- 信息量:信息论中的一个度量
- 信息量应该为正数;
- 一个事件的信息量和它发生的概率成反比;
- 信息熵(Entropy):集合的 纯净度的一个指标
- 一个集合里的元素全部是属于同一个分组,这个时候就表示最纯净,我们就说熵为 0;
- 如果这个集合里的元素是来自不同的分组,那么熵是大于 0 的值。其具体的计算公式 如下:
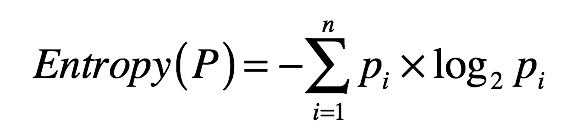
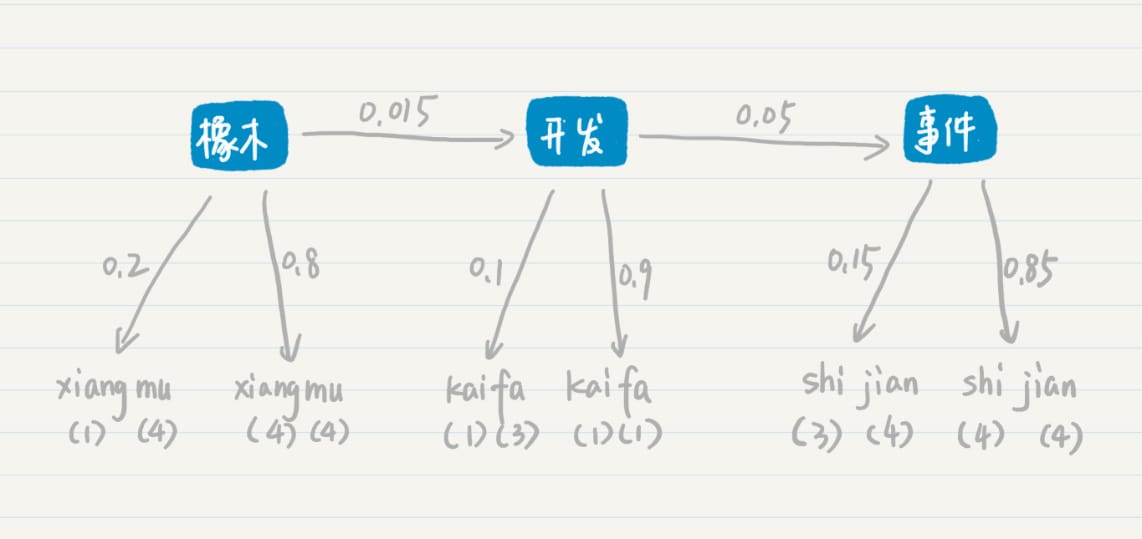
一个集合中所包含的分组越多、元素在这些分组里分布 得越均匀,熵值也越大。
而熵值表示了纯净的程度,或者从相反的角度来说,是混乱的程 度。
信息量期望
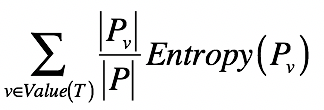
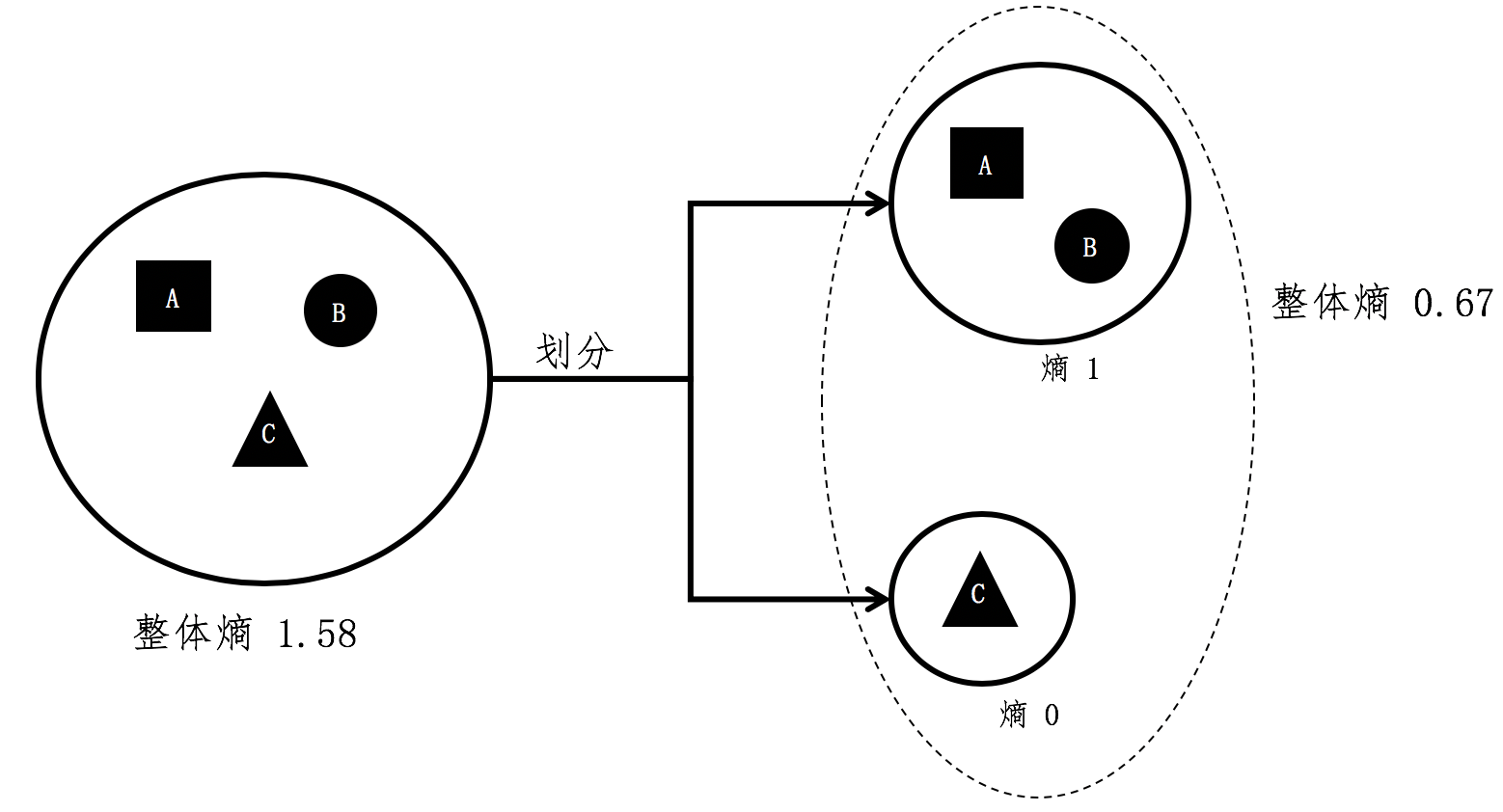
对于多个小集合而言,其整体的熵等于各个小集合之熵的加权平均。
- 信息增益(Information Gain):划分后整体熵的下降
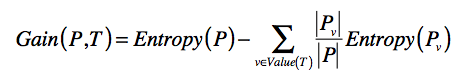
决策树
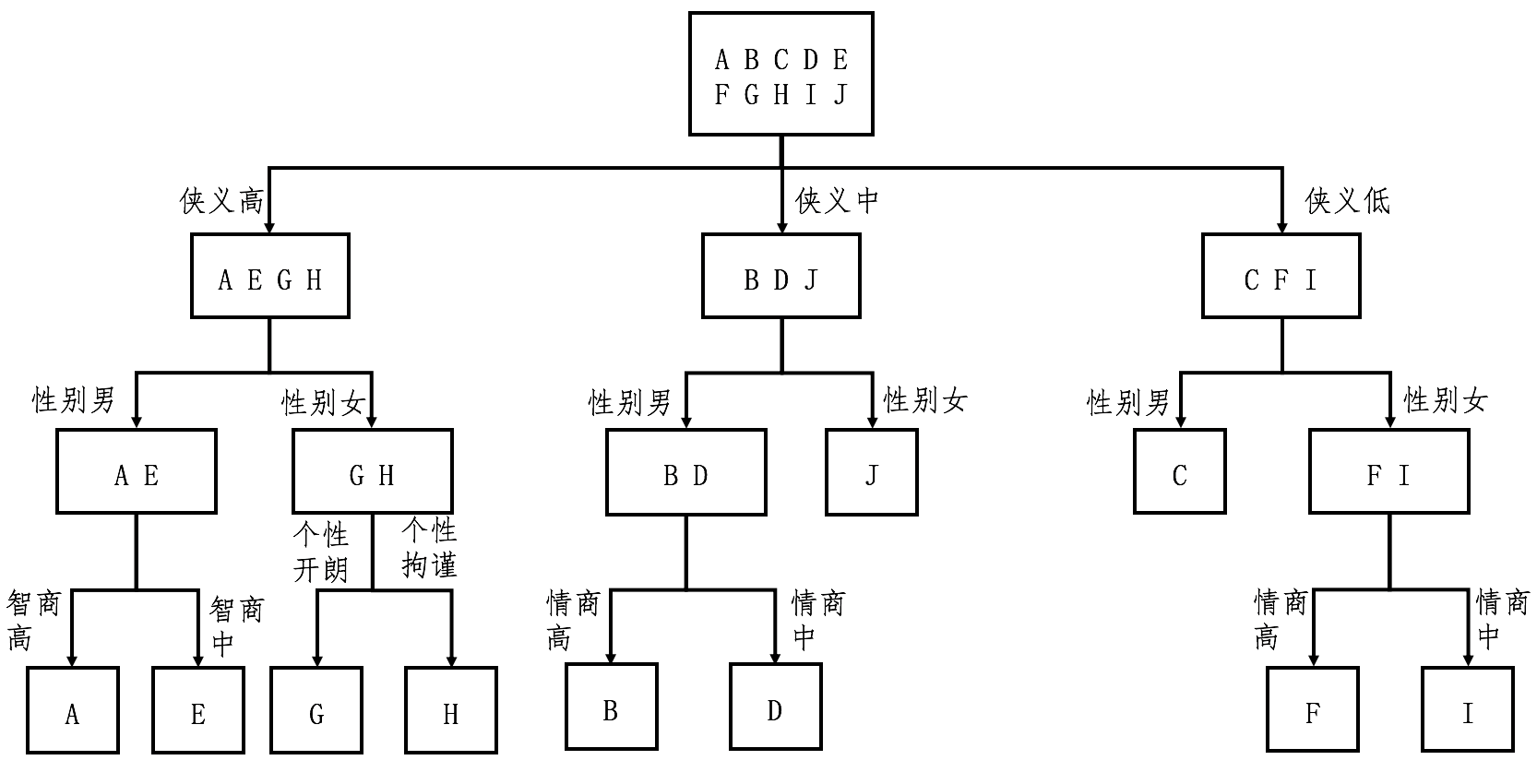
- 第一步,根据集合中的样本分类,为每个集合计算信息熵,并通过全部集合的熵之加权平 均,获得整个数据集的熵。注意,一开始集合只有一个,并且包含了所有的样本。
- 第二步,根据信息增益,计算每个特征的区分能力。挑选区分能力最强的特征,并对每个 集合进行更细的划分。
- 第三步,有了新的划分之后,回到第一步,重复第一步和第二步,直到没有更多的特征, 或者所有的样本都已经被分好类。
- ID3(Iterative Dichotomiser 3,迭代二叉树 3 代)
- 信息增益
- 优先考虑具有较多取值的特征
- C4.5 算法
- 信息增益率(Information Gain Ratio)
- 分裂信息(Split Information)
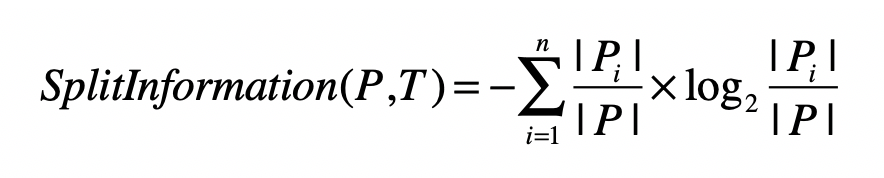
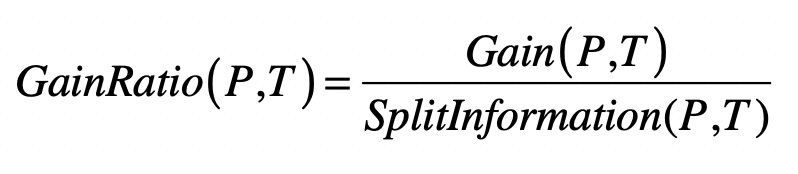
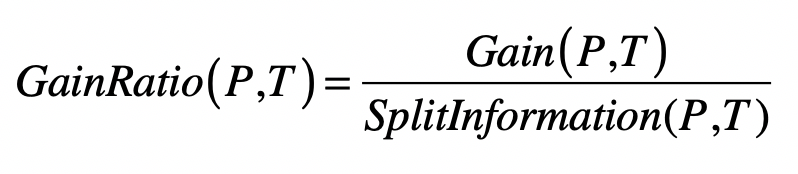
- CART 算法(Classification and Regression Trees,分类与回归 树)
- 基尼指数(Gini)
- 二叉树
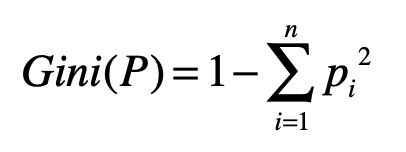
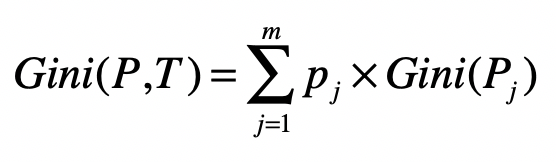
- 优化
- 剪枝
- 预剪枝
- 后剪枝
- 随机森林
- 剪枝
熵、信息增益和卡方
利用卡方检验进行特征选择
如果两者独立,证明特征和分类没有明显的相关性,特征对于分类来说没有提供足够的信息量。
归一化和标准化
为什么需要特征变换?
- 线性回归模型:因变量和自变量为线性关系
- 非线性回归分析模型:因变量和自变量为非线性关系
多元线性回归
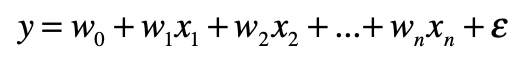
两种常见的特征变换方法
- 归一化(Normalization)。
它其实就是获取原始数据的最大值和最小值,然后把原始值线性变换到 [0,1] 之间
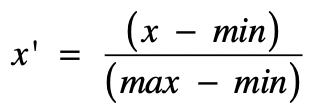
- 标准化
基于正态分布的 z 分数(z-score)标准化(Standardization)。
该方法假设数据呈现标准正态分布。
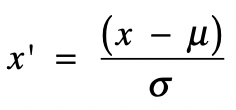
\[ x^{\prime}=\frac{(x-\mu)}{\sigma} \]
其中 \(x\) 为原始值,\(\mu\) 为均值,\(\sigma\) 为标准差,\(x^{\prime}\) 是变换后的值。
统计意义
A/B 测试
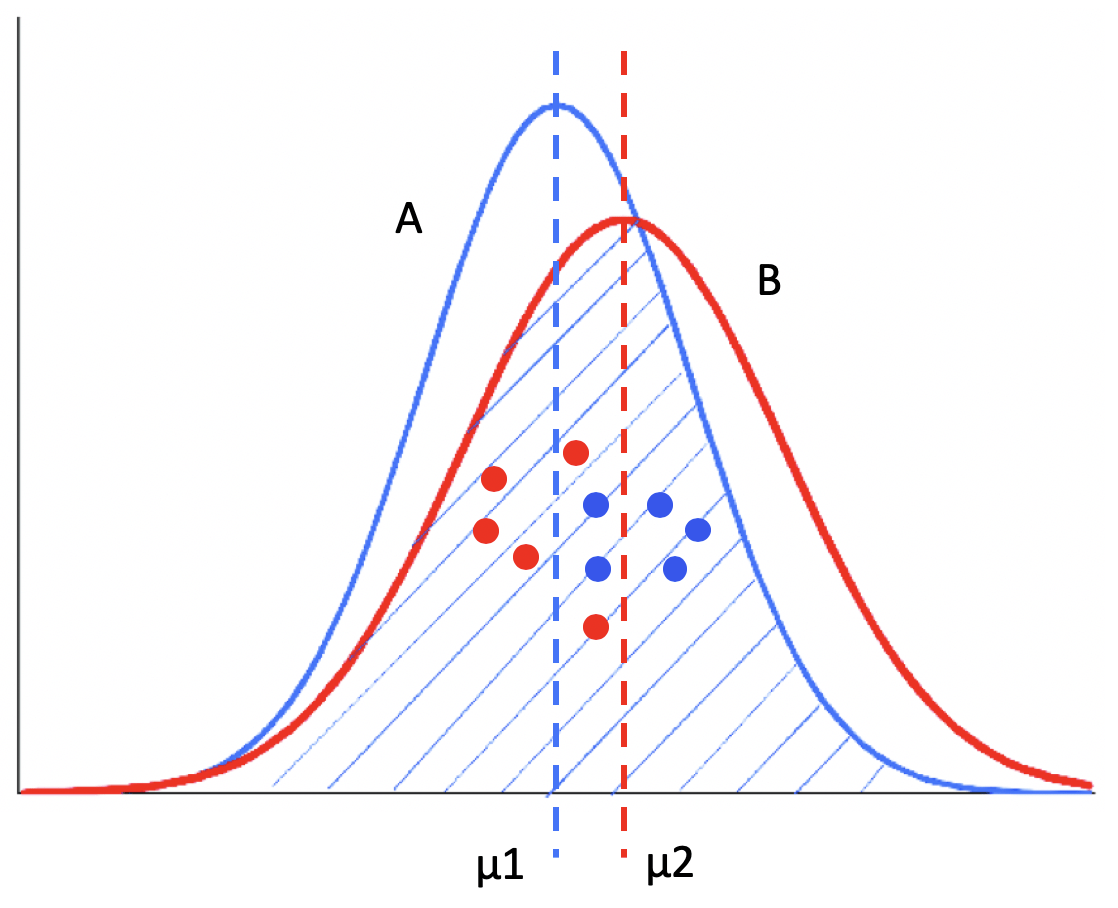
显著性差异(Significant Difference)
- 第一,两个分布之间的差异。
- “有显著性差异”
- 第二,采样引起的差异。
- “无显著性差异”
“具有显著性差异”,称为“差异具有统计意义”或者“差异具有显著性”
统计假设检验和显著性检验
统计假设检验是指事先对随机变量的参数或总体分布做出一个假设,然后利用样本信息来 判断这个假设是否合理。
在统计学上,我们称这种假设为虚无假设(Null Hypothesis),也叫原假设或零假设,通常记作 H0。
而和虚无假设对立的假设,我们称为对立假设(Alternative Hypothesis),通常记作 H1。也就是说,如果证明虚无假设不成立,那么就可以推出对立假设成立。
通常我们把概率不超 过 0.05 的事件称为“小概率事件”
P 值(P-value)
P 值中的 P 代表 Probability,就是当 H0 假 设为真时,样本出现的概率,或者换句话说,其实就是我们所观测到的样本数据符合原假 设 H0 的可能性有多大。
方差分析
方差分析(Analysis of Variance, ANOVA),也叫 F检验。
- 随机性:样本是随机采样的;
- 独立性:来自不同组的样本是相互独立的;
- 正态分布性:组内样本都来自一个正态分布;
- 方差齐性:不同组的方差相等或相近。
自由度(degree of freedom),英文缩写是 df,它是指采样中能够自由变化的数据个 数。
拟合
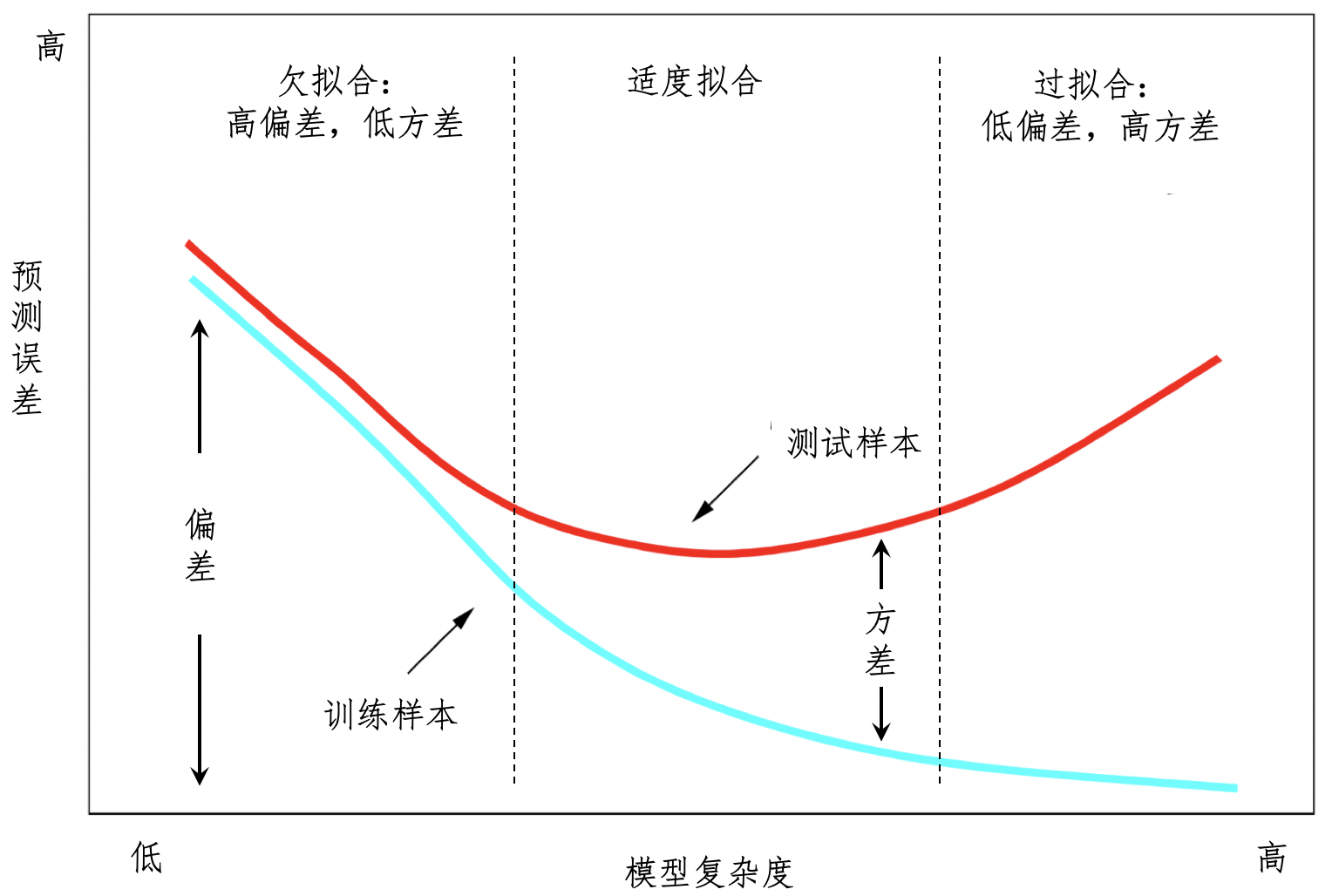
- 欠拟合问题 产生的主要原因 是特征维度过少,拟合的模型不够复杂,无法满足训练样本,最终导致误差较大。
- 过拟合问题 产生的主要原因则是特征维度过多,导致拟合的模型过于完美地符 合训练样本,但是无法适应测试样本或者说新的数据。
交叉验证(Cross Validation)的划分方式来保持训练数 据和测试数据的一致性。
线性代数
线性代数
向量和向量空间
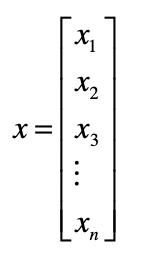
向量的每个元素就代表 一维特征,而元素的值代表了相应特征的值,我们称这类向量为 特征向量(Feature Vector)。
矩阵的特征向量(Eigenvector)
向量的运算
- 加法
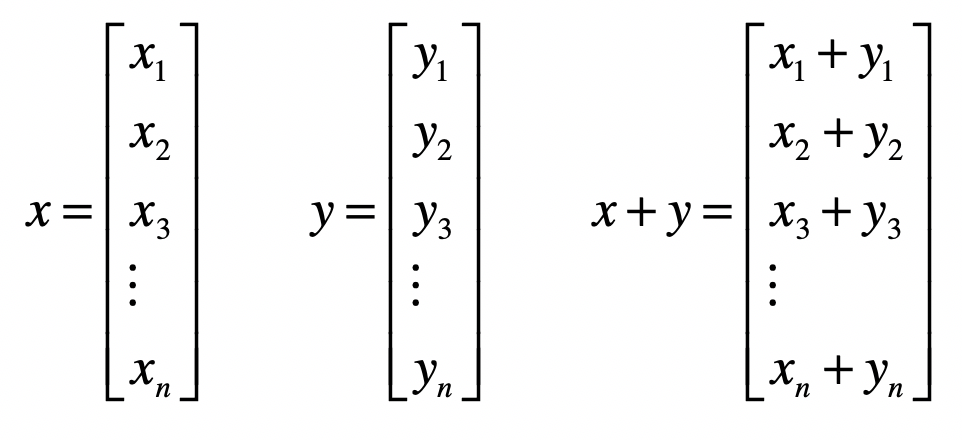
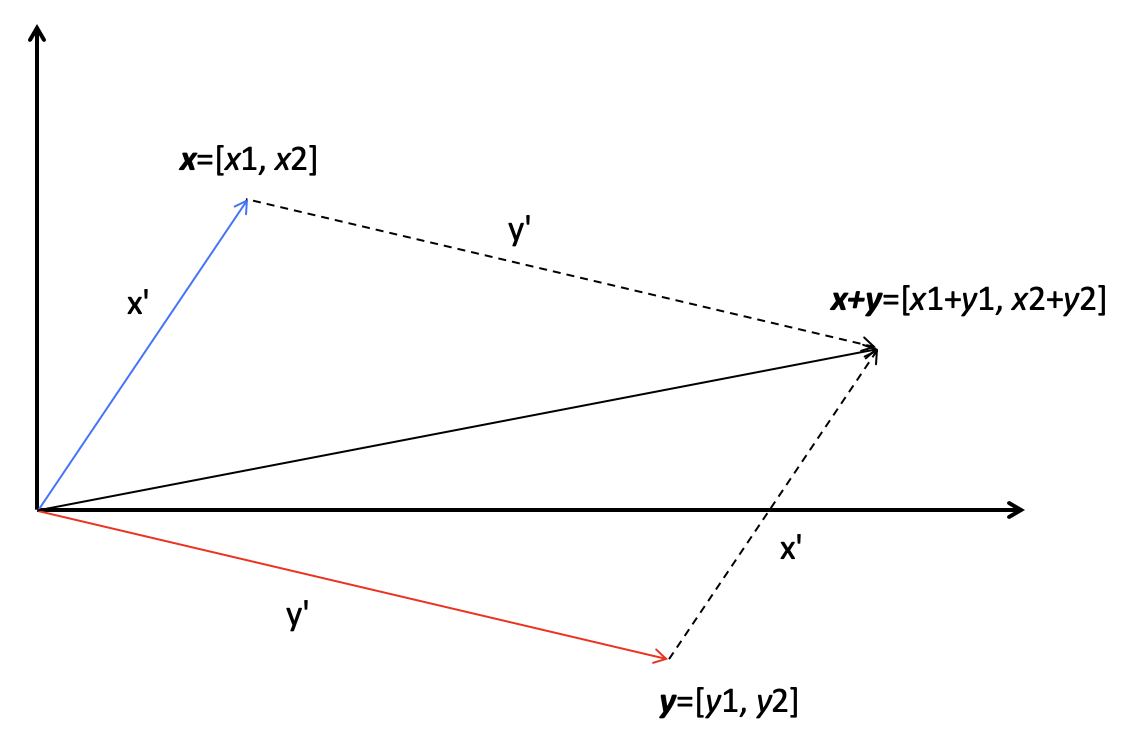
- 乘法(或点乘)
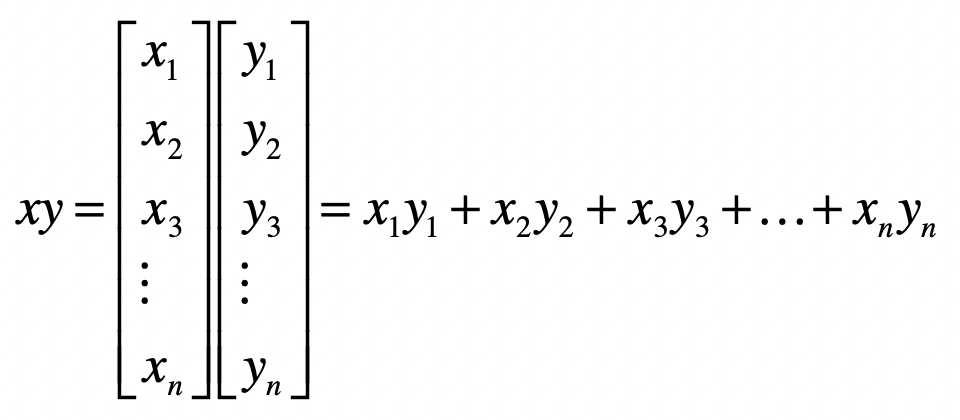
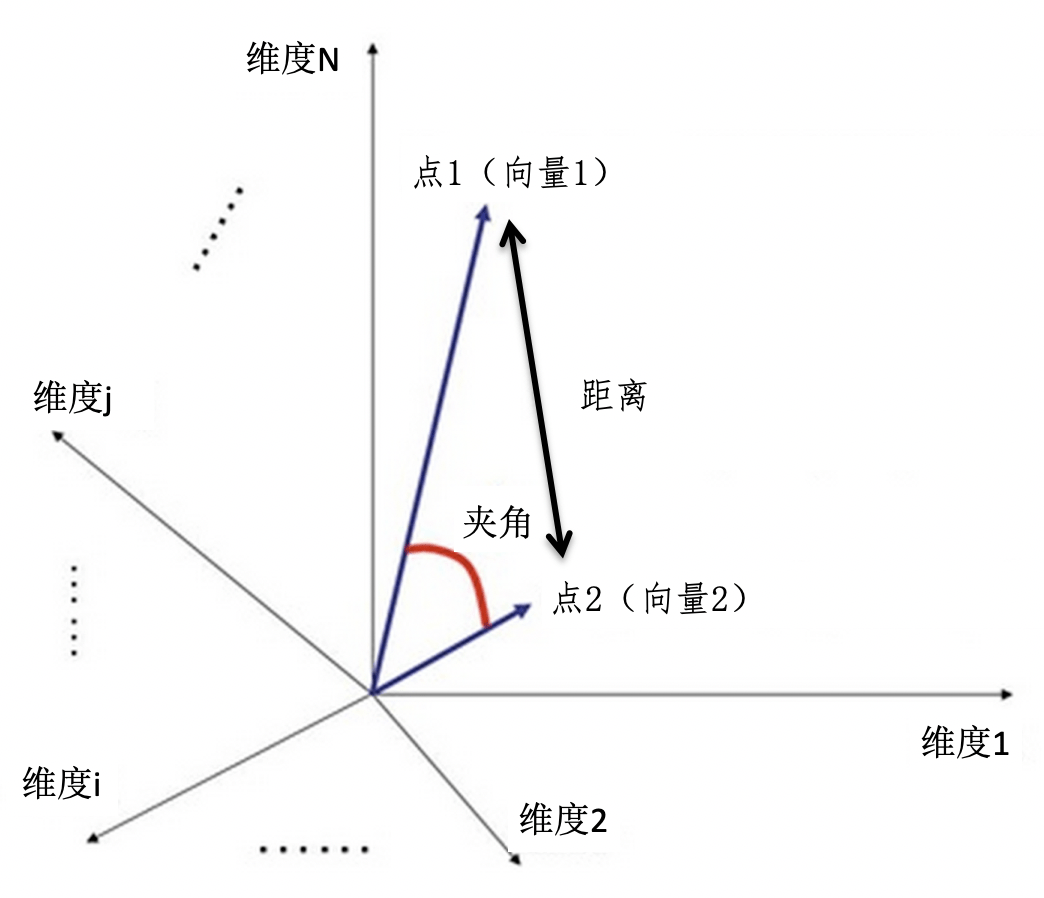
- 距离
- 夹角
矩阵的运算
矩阵由多个长度相等的向量组成,其中的每列或者每行就是一个向量。
因此,我们把向量延伸一下就能得到矩阵(Matrix)。
矩阵乘法
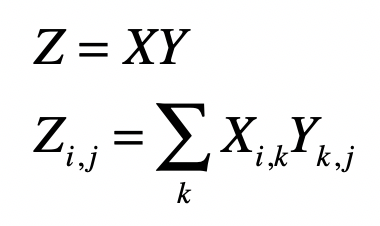
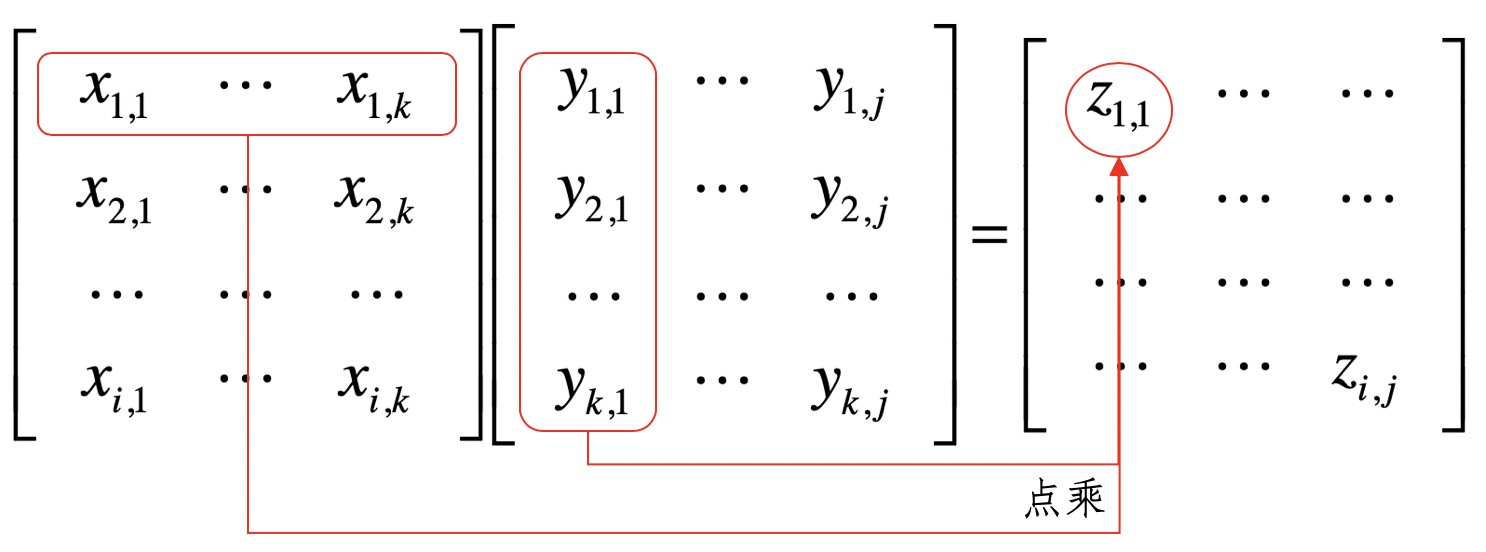
两个矩阵中对应元素进行相乘,称它为 元素对应乘积,或者 Hadamard 乘积
转置(Transposition)是指矩阵内的元素行索引和纵索引互换
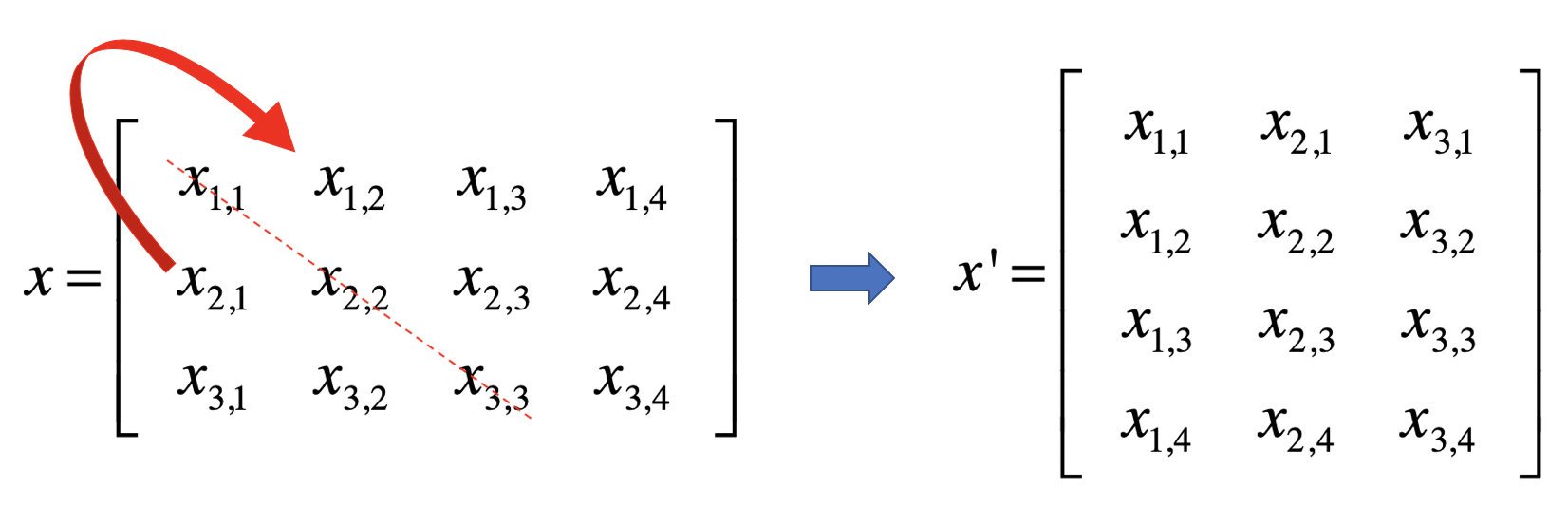
单位矩阵(Identity Matrix)
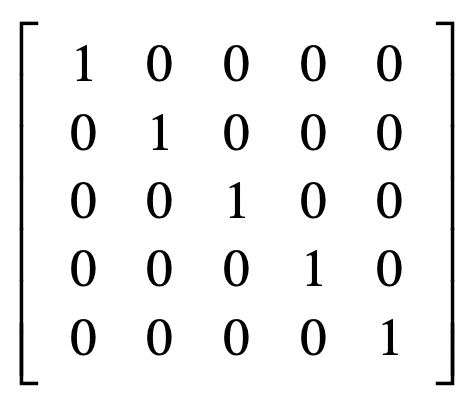
矩阵逆(Matrix Inversion)
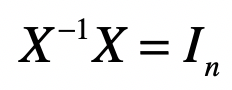
向量空间模型
向量之间的距离
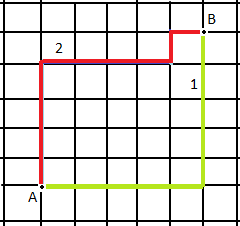
- 曼哈顿距离(Manhattan Distance)
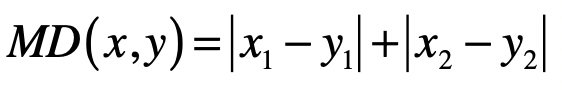
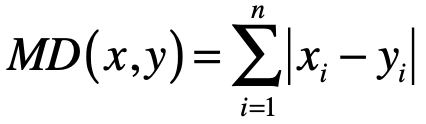
- 欧氏距离(Euclidean Distance)
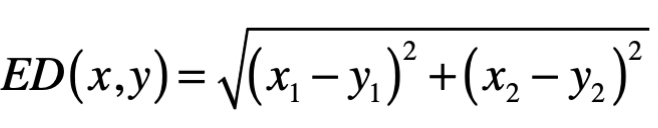
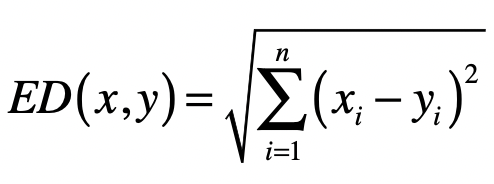
- 切比雪夫距离(Chebyshev Distance)
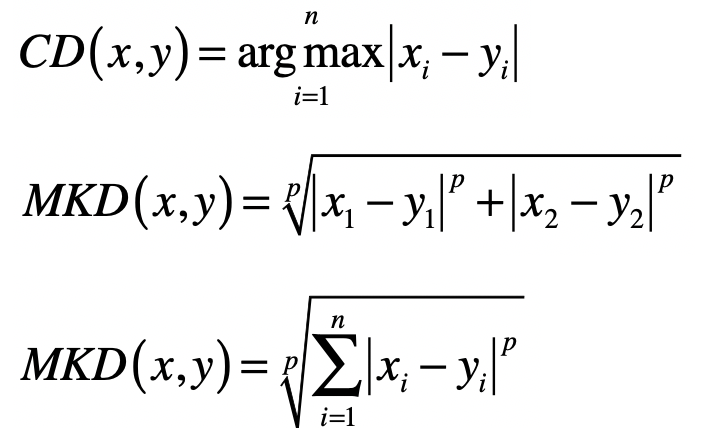
向量的长度
- \(L_{1}\) 范数 \(\|x\|\) ,它是为 \(x\) 向量各个元素绝对值之和,对应于向量和原点之间的曼哈顿距离。
\(L_{2}\) 范数 \(\|x\|_2\) ,它是向量 \(x\) 各个元素平方和的 \(\frac{1}{2}\) 次方,对应于向量 \(x\) 和原点之间的欧氏距离。
\(L_{p}\) 范数 \(\|x\|_p\) ,为向量各个元素绝对值 \(p\) 次方和的 \(1/p\) 次方,对应于向量 \(x\) 和原点之间的闵氏距离。
\(L_{\infty}\) 范数 \(\|x\|_{\infty}\),为 \(x\) 向量各个元素绝对值最大那个元素的绝对值,对应于向量 \(x\) 和原点之间的切比雪夫距离。
所以,在讨论向量的长度时,我们需要弄清楚是 L几范数。
向量之间的夹角
\[ \operatorname{cosine}(X, Y)=\frac{\sum_{i=1}^{n}\left(x_{i} \times y_{i}\right)}{\sqrt{\sum_{i=1}^{n} x_{i}^{2} \times \sum_{i=1}^{n} y_{i}^{2}}} \]
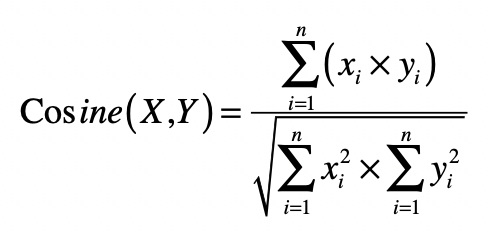
向量空间模型(Vector Space Model)
文本检索
信息检索就是让计算机根据用户信息需求,从大规模、非结构化的数据中,找 出相关的资料。
信息检索中的向量空间模型
- 第一步,把文档集合都转换成向量的形式。
- 第二步,把用户输入的查询转换成向量的形式,然后把这个查询的向量和所有文档的向 量,进行比对,计算出基于距离或者夹角余弦的相似度。
- 第三步,根据查询和每个文档的相似度,找出相似度最高的文档,认为它们是和指定查询 最相关的。
- 第四步,评估查询结果的相关性。
文本聚类
聚类算法
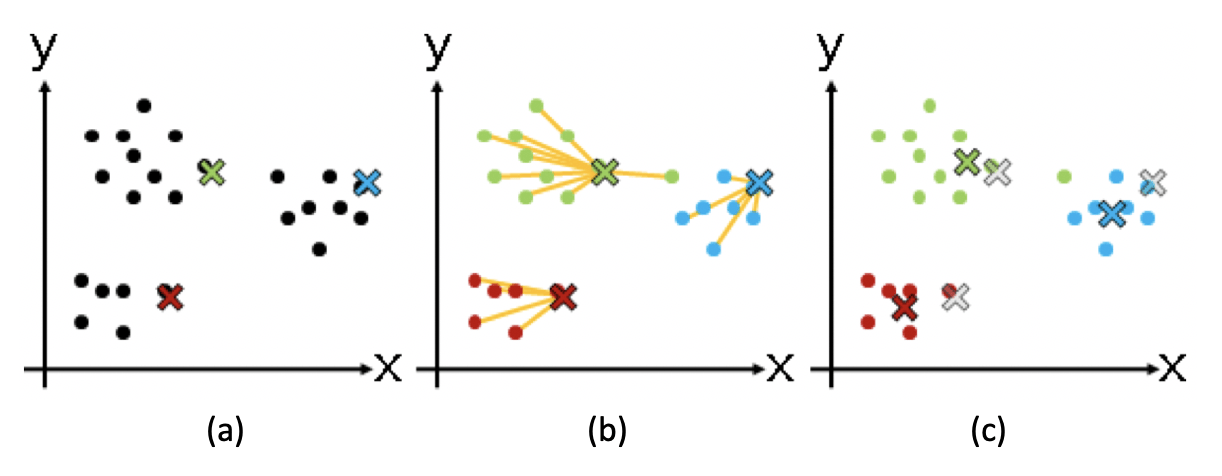
K 均值(K-Means)聚类算法
尽量最大化总的 群组内相似度,同时尽量最小化群组之间的相似度。
- 从 N 个数据对象中随机选取 k 个对象作为质心,这里每个群组的质心定义是,群组内 所有成员对象的平均值。因为是第一轮,所以第 i 个群组的质心就是第 i 个对象,而且 这时候我们只有这一个组员。
- 对剩余的对象,测量它和每个质心的相似度,并把它归到最近的质心所属的群组。这里 我们可以说距离,也可以说相似度,只是两者呈现反比关系。
- 重新计算已经得到的各个群组的质心。这里质心的计算是关键,如果使用特征向量来表 示的数据对象,那么最基本的方法是取群组内成员的特征向量,将它们的平均值作为质心的向量表示。
- 迭代上面的第 2 步和第 3 步,直至新的质心与原质心相等或相差之值小于指定阈值,算法结束。
矩阵
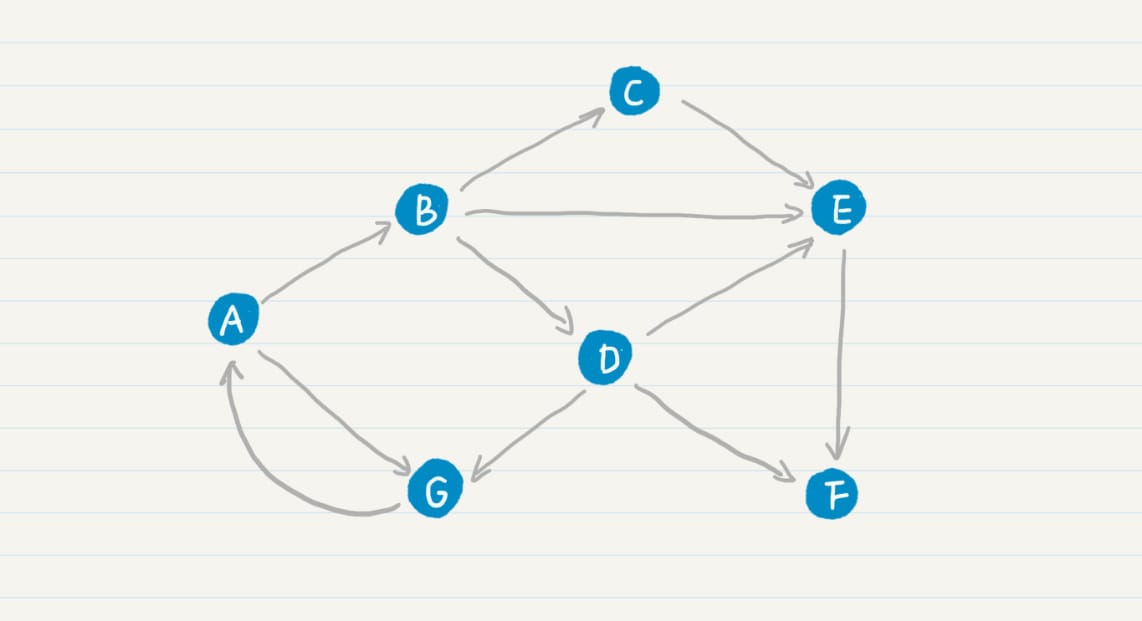
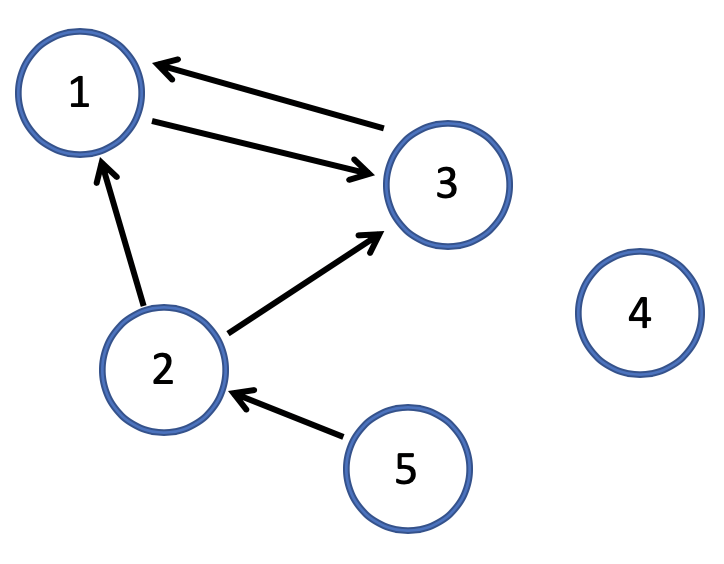
PageRank 链接分析算法
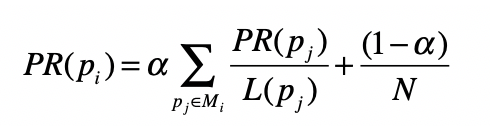
简化 PageRank 公式
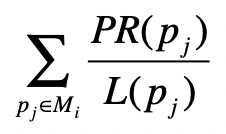
矩阵点乘
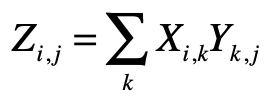
拓扑图
原始矩阵
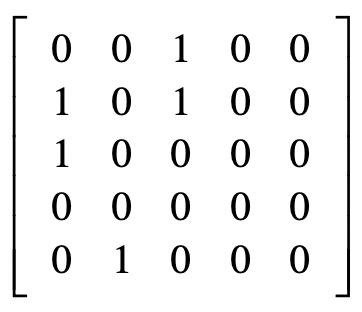
归一化
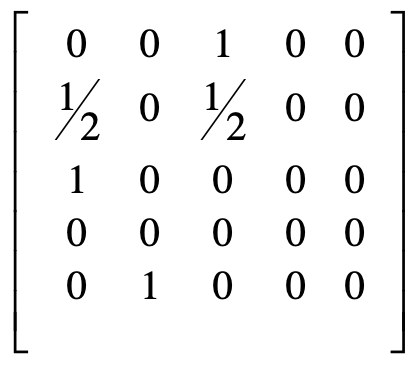
初始值都设为 1
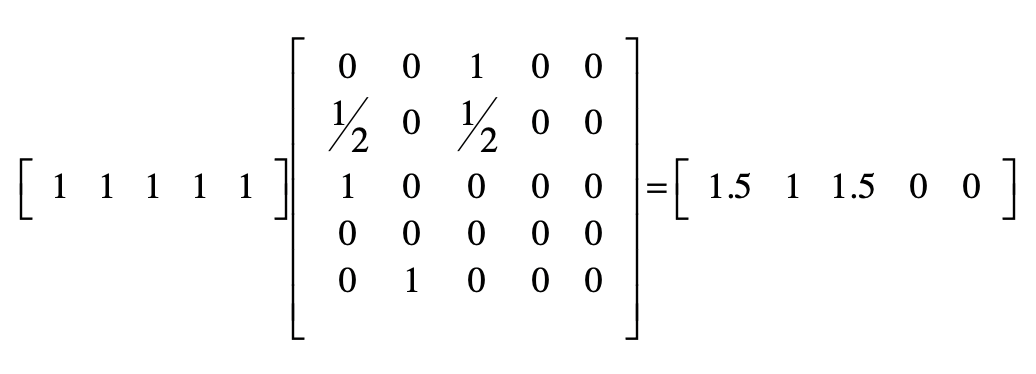
考虑随机跳转
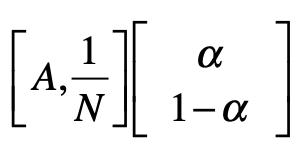
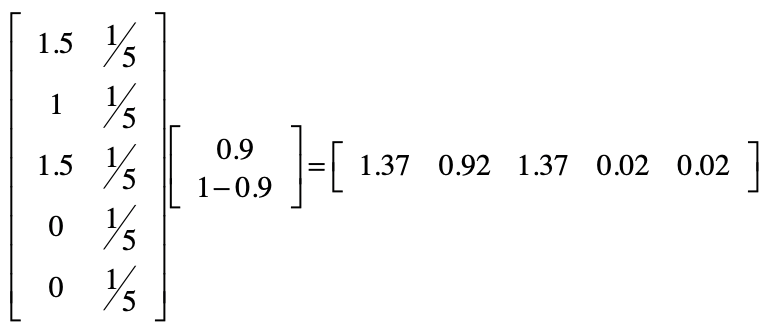
用矩阵实现推荐系统的核心思想

基于用户的过滤
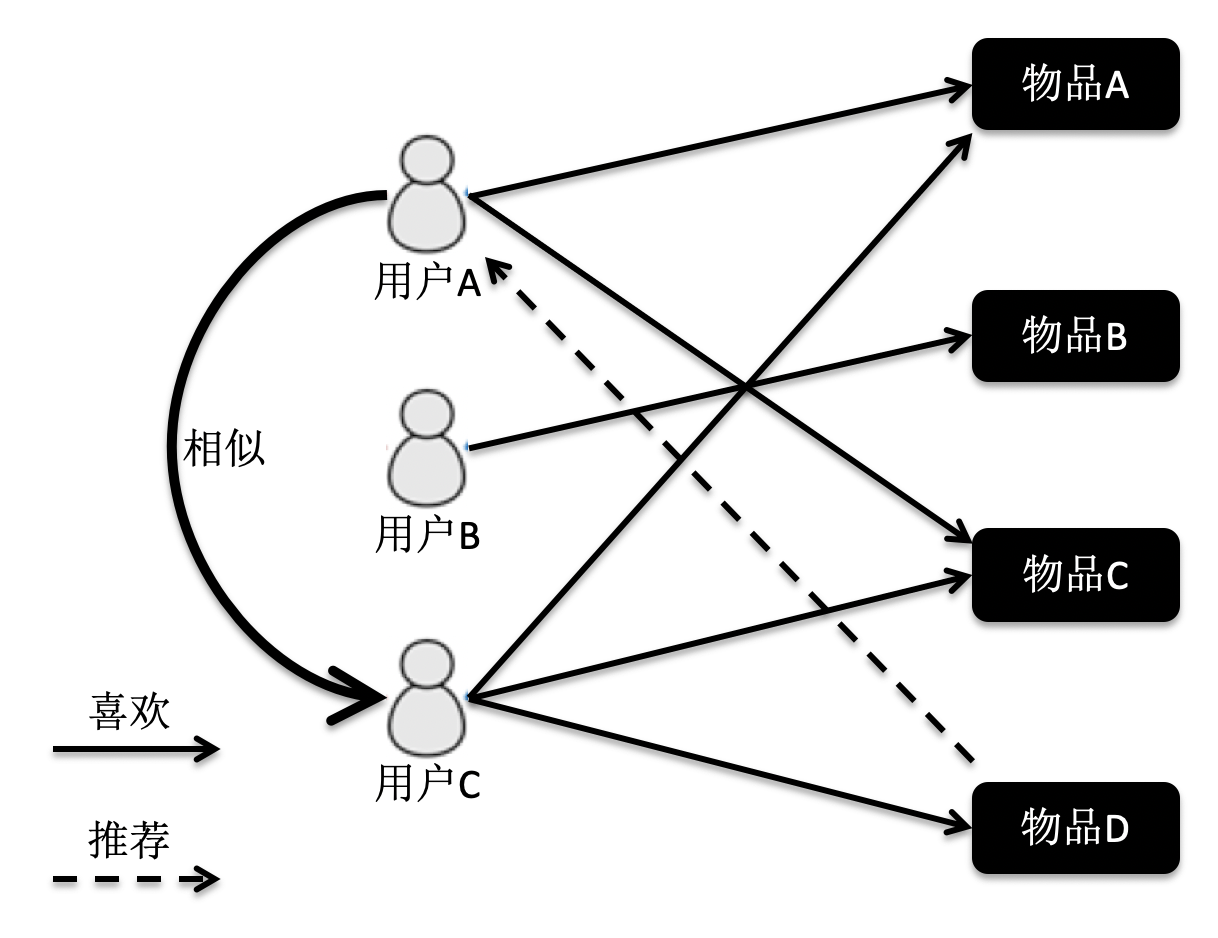
基于物品的过滤
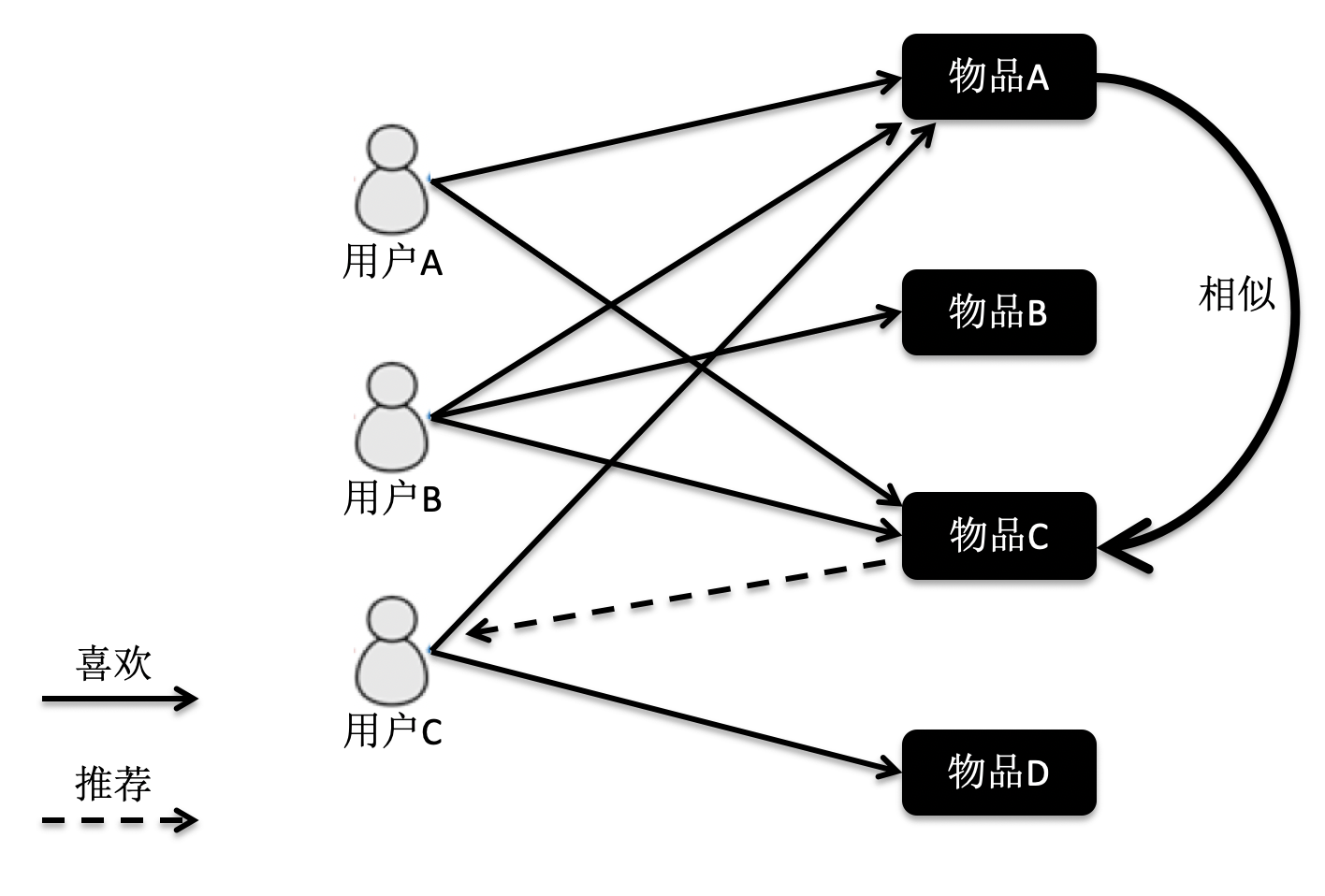
线性回归
\[ \begin{aligned} &2 x_{1}+x_{2}+x_{3}=0\\ &4 x_{1}+2 x_{2}+x_{3}=56\\ &2 x_{1}-x_{2}+4 x_{3}=4 \end{aligned} \]
高斯消元法
使用矩阵实现高斯消元法
系数矩阵
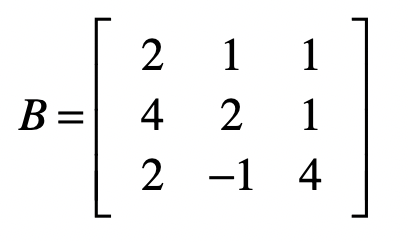
消元
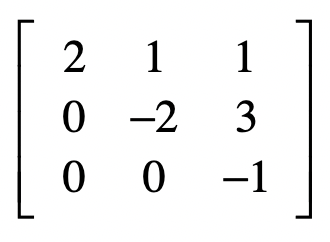
系数
\[ \begin{array}{l} 1 \cdot x_{1}+0 \cdot x_{2}+0 \cdot x_{3}=71 \\ 0 \cdot x_{1}+1 \cdot x_{2}+0 \cdot x_{3}=-86 \\ 0 \cdot x_{1}+0 \cdot x_{2}+1 \cdot x_{3}=-56 \end{array} \]
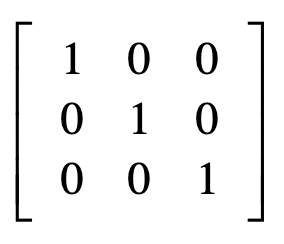
增广矩阵
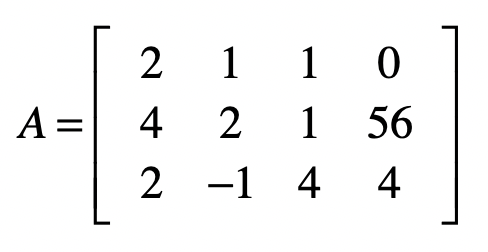
线性回归
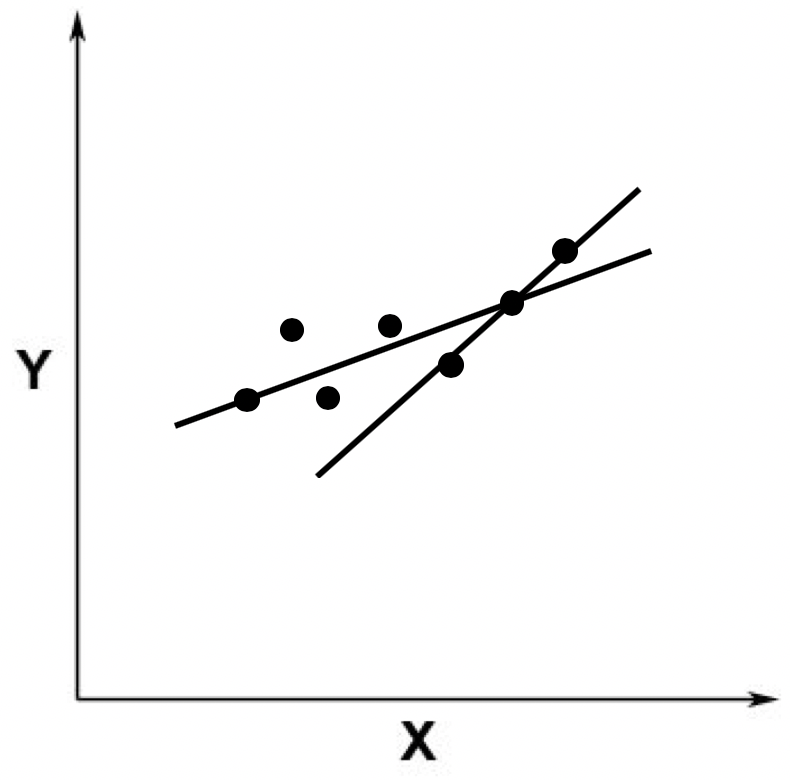
最小二乘法
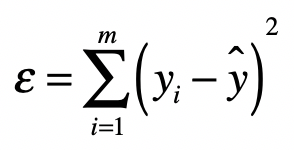
PCA主成分分析(Principal Component Analysis)
标准化样本矩阵中的原始数据;
获取标准化数据的协方差矩阵;
计算协方差矩阵的特征值和特征向量;
依照特征值的大小,挑选主要的特征向量; 5. 生成新的特征。
标准化原始数据
\[ x^{\prime}=\frac{x-\mu}{\sigma} \]
- 获取协方差矩阵
- 协方差(Covariance):衡量两个变 量的总体误差
\[ \operatorname{cov}(x, y)=\frac{\sum_{k=1}^{m}\left(x_{k}-\bar{x}\right)\left(y_{k}-\bar{y}\right)}{m-1} \]
- 协方差矩阵
\[ \operatorname{cov}\left(X_{, i}, X_{, j}\right)=\frac{\sum_{k=1}^{m}\left(x_{k, i}-\bar{X}_{, i}\right)\left(x_{k, j}-\bar{X}_{, j}\right)}{m-1} \]
\[ C O V=\left[\begin{array}{ccccc} \operatorname{cov}\left(X_{1}, X_{1}\right) & \operatorname{cov}\left(X_{1}, X_{2}\right) & \cdots & \operatorname{cov}\left(X_{1}, X_{n-1}\right) & \operatorname{cov}\left(X_{1}, X_{n}\right) \\ \operatorname{cov}\left(X_{2}, X_{1}\right) & \operatorname{cov}\left(X_{2}, X_{2}\right) & \cdots & \operatorname{cov}\left(X_{2}, X_{n-1}\right) & \operatorname{cov}\left(X_{2}, X_{n}\right) \\ \cdots & \cdots & \cdots & \cdots & \cdots \\ \operatorname{cov}\left(X_{n}, X_{1}\right) & \operatorname{cov}\left(X_{n}, X_{2}\right) & \cdots & \operatorname{cov}\left(X_{n}, X_{n-1}\right) & \operatorname{cov}\left(X_{n}, X_{n}\right) \end{array}\right] \]
- 计算协方差矩阵的特征值和特征向量
\[ X v=\lambda v \]
特征 值的推导过程
\[ \begin{aligned} &X v=\lambda v\\ &X v-\lambda v=0\\ &X v-\lambda I v=0\\ &(X-\lambda I) v=0 \end{aligned} \]
矩阵的行列式
\[ |(X-\lambda I)|= \left| \left[ \begin{array}{cccccc} x_{1,1}-\lambda & x_{1,2} & x_{1,3} & \cdots & x_{1, n-1} & x_{1, n} \\ x_{2,1} & x_{2,2}-\lambda & x_{2,3} & \cdots & x_{2, n-1} & x_{2, n} \\ x_{3,1} & x_{3,2} & x_{3,3}-\lambda & \cdots & x_{3, n-1} & x_{3, n} \\ \cdots & \cdots & \cdots & \cdots & \cdots & \cdots \\ x_{n-1,1} & x_{n-1,2} & x_{n-1,3} & \cdots & x_{n-1, n-1}-\lambda & x_{n-1, n} \\ x_{n, 1} & x_{n, 2} & x_{n, 3} & \cdots & x_{n, n-1} & x_{n, n}-\lambda \end{array}\right] \right| =0 \]
\[ (\lambda I-X)\left[\begin{array}{l} x_{1} \\ x_{2} \\ \dots \\ x_{n} \end{array}\right] \]
- 挑选主要的特征向量,转换原始数据
SVD 奇异值分解(Singular Value Decomposition)
方阵的特征分解
方阵(Square Matrix) 是一种特殊的矩阵,它的行数和列数相等。如果一个矩阵的行数和列数 都是 n,那么我们把它称作 n 阶方阵。
如果一个矩阵和其转置矩阵相乘得到的是单位矩阵,那么它就是一个 酉矩阵(Unitary Matrix)。
\[ X^{\prime} X=I \]
其中 X’表示 X 的转置,I 表示单位矩阵。
换句话说,矩阵 X 为酉矩阵的充分必要条件是 X 的转 置矩阵和 X 的逆矩阵相等。
\[ X^{\prime}=X^{-1} \]
特征分解(Eigendecomposition)
\[ \begin{aligned} &X V V^{-1}=V \Sigma V^{-1}\\ &X I=V \Sigma V^{-1}\\ &X=V \Sigma V^{-1} \end{aligned} \]
主要考量因素
- 硬件的性能
- 命中率
- 更新周期
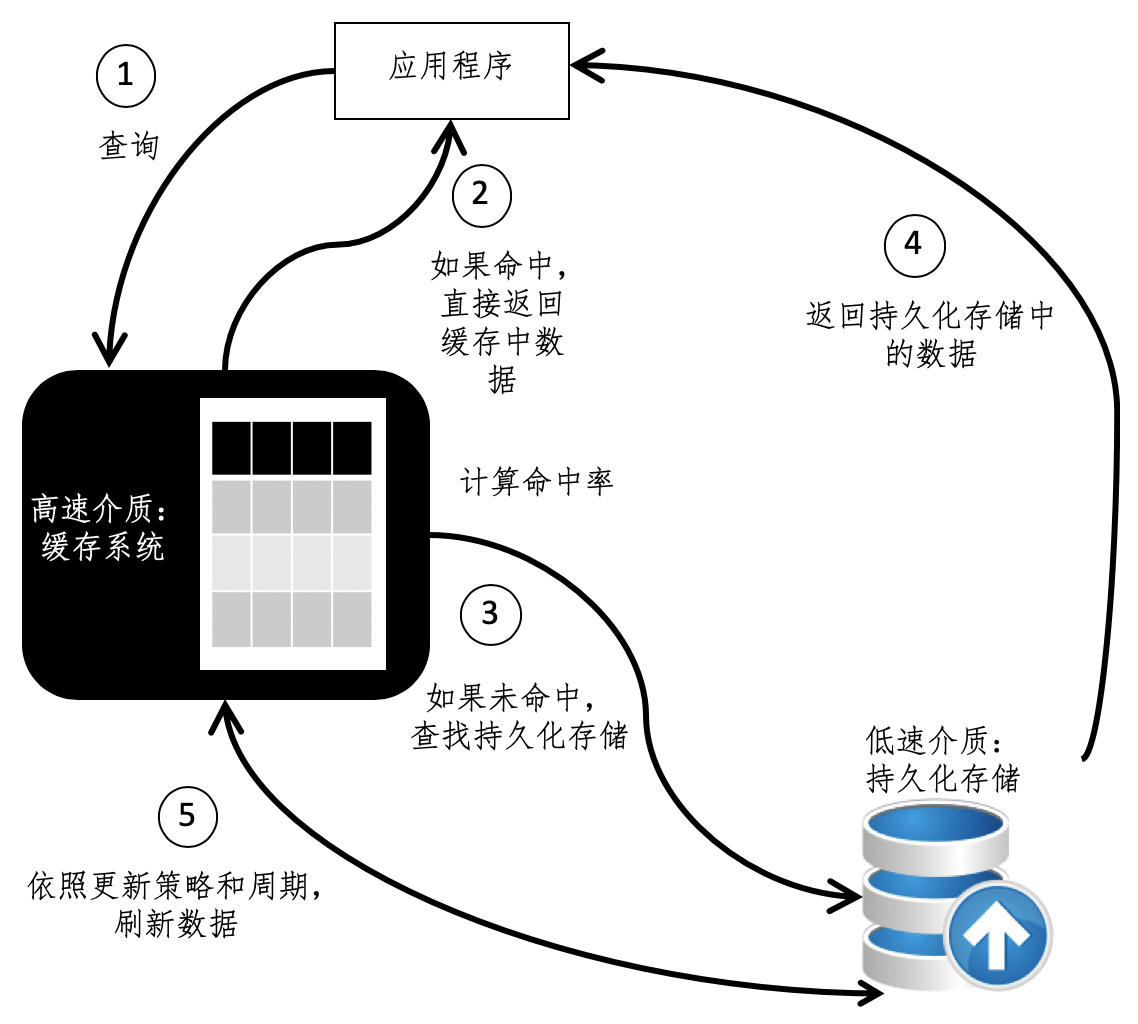
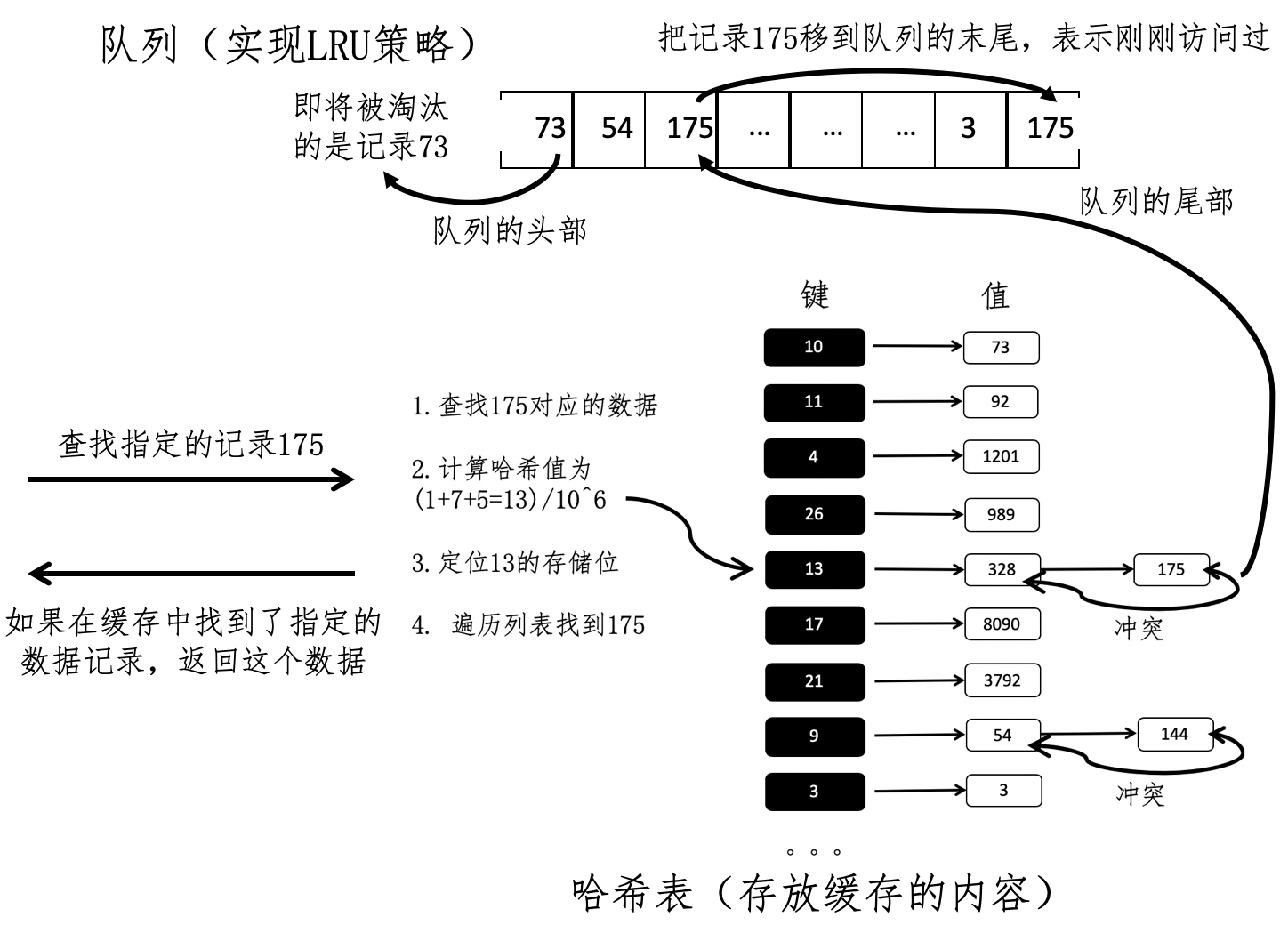
搜索引擎
搜索引擎的设计框架
- 离线的预处理
- 在线的查询
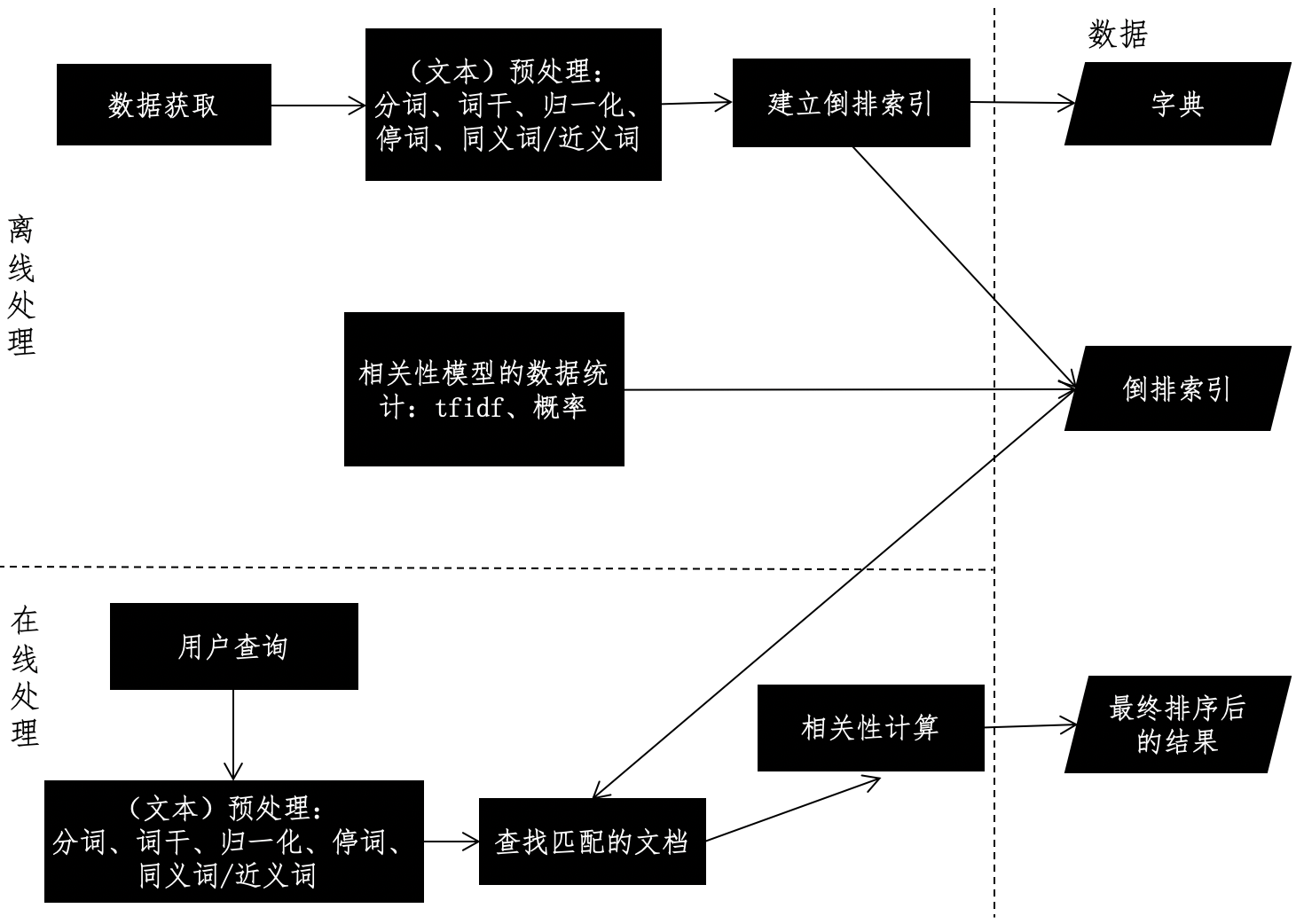
倒排索引的设计
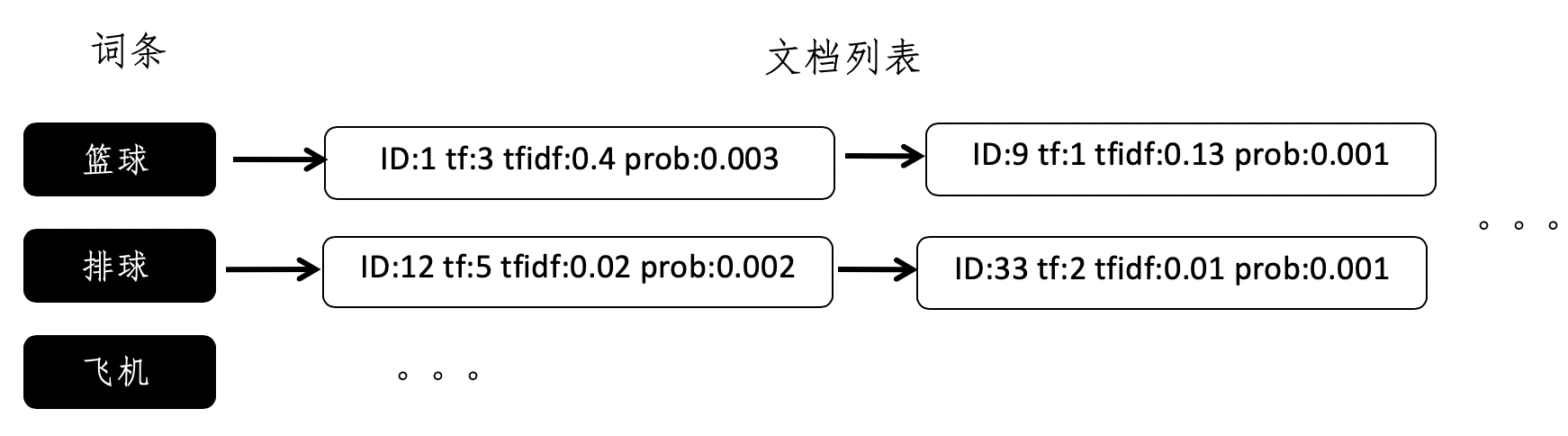
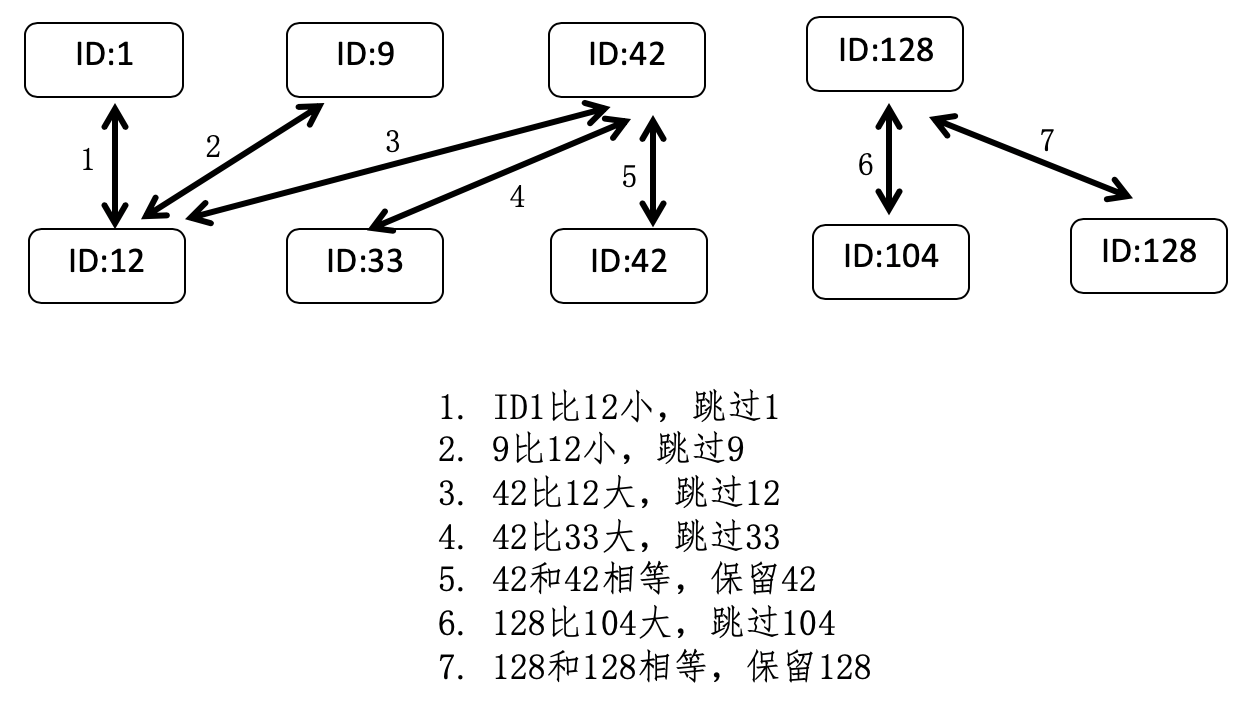
向量空间和倒排索引的结合
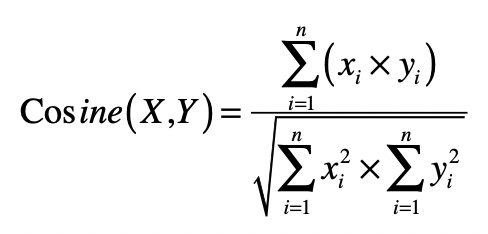
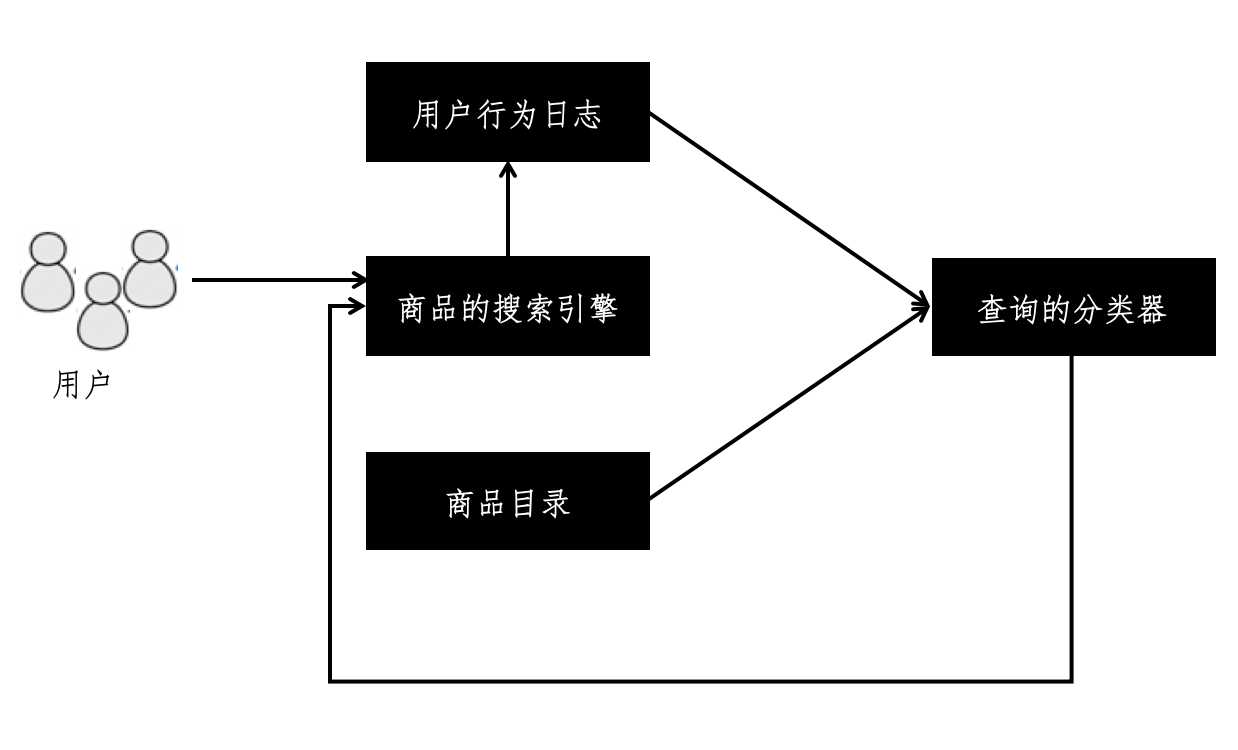
查询分类和搜索引擎的结合
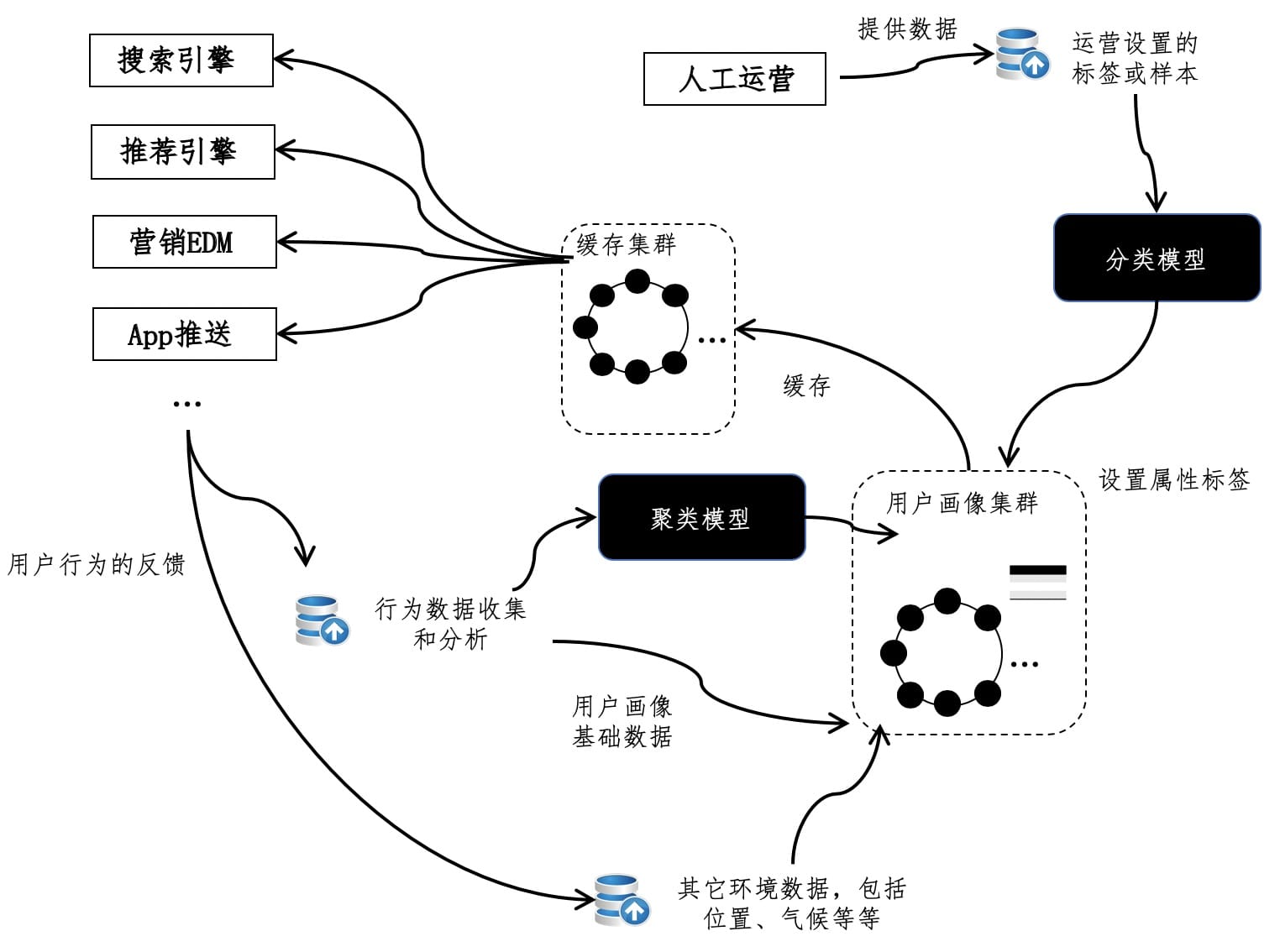
推荐系统
程序员需要读哪些数学书?
基础思想篇推荐书籍:《离散数学及其应用》

概率统计篇推荐书籍:《概率统计》

线性代数篇推荐书籍:《线性代数及其应用》

入门、通识类书籍推荐:《程序员的数学》
《程序员的数学》
《程序员的数 学:概率统计》
《程序员的数学:线性代数》

计算机领域:《数学之美》
