统计学习方法

《统计学习方法》第 14 章 聚类方法 KMeans

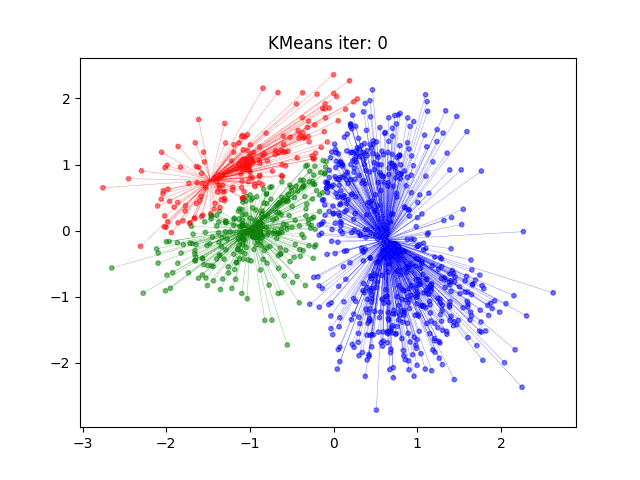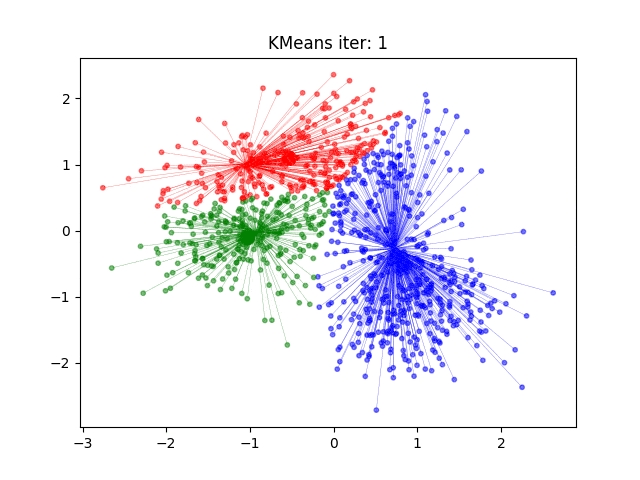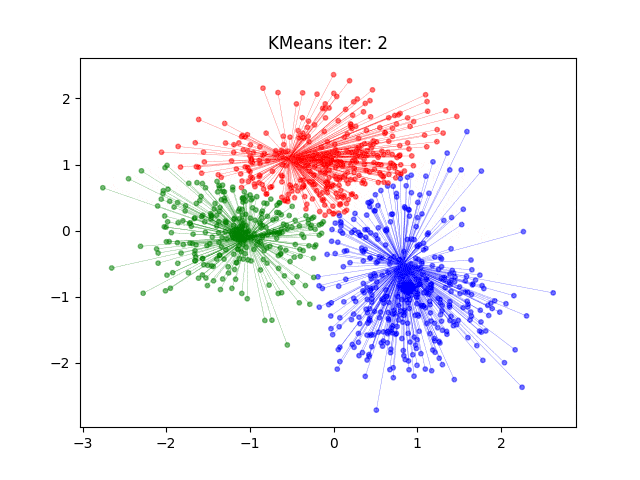
k-均值聚类

n 个样本分到 k 个不同的类或簇，每个样本到其所属类的中心的距离最小。

每个样本只能属于一个类，所有 k-均值聚类 是 硬聚类。

模型

  • k < n

\[ G_{i} \cap G_{j} = \varnothing, \bigcup_{i=1}^{k}G_{i} = X \]

策略

  • 距离： 欧式距离
  • 损失函数：样本与所属类的中心的距离总保
  • NP 困难问题

算法

目标函数极小化

  1. 初始化，随机取 $ k $ 个样本做中心
  2. 对样本进行聚类，计算样本到类中心距离，每个样本指派到与其最近的中心的类
  3. 计算新的类中心。对聚类结果计算样本的均值，做为新的类中心
  4. 如果迭代收敛或符合停止条件，输出。否则，令 $ t = t + 1 $ ，返回 2
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
def fit(self, X):
    self._setup_input(X)
    n_samples, _ = X.shape
    # 从 X 中随机获取 k 个元素做中心
    self._centers = np.array(
        random.sample(list(np.unique(X, axis=0)), self.k))

    old_clusters = None
    n_iters = 0

    while True:
        new_clusters = [self._min_k(x) for x in X]

        if new_clusters == old_clusters:
            print("Training finished after {n_iters} iterations!".format(n_iters=n_iters))
            return

        old_clusters = new_clusters
        n_iters += 1

        for cluster_i in range(self.k):
            # 计算新的中心
            points_idx = np.where(np.array(new_clusters) == cluster_i)
            xi = X[points_idx]
            self._centers[cluster_i] = xi.mean(axis=0)

        self._centers_list.append(np.copy(self._centers))

源码：https://github.com/iOSDevLog/slmethod