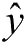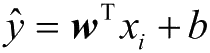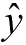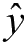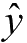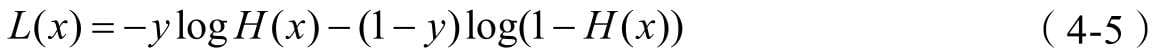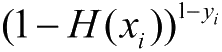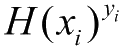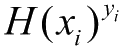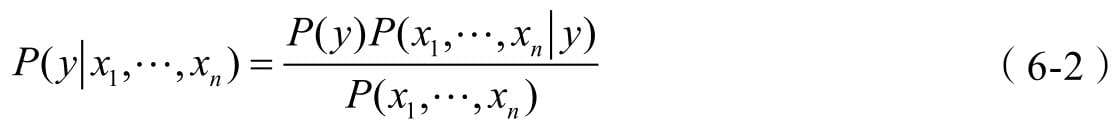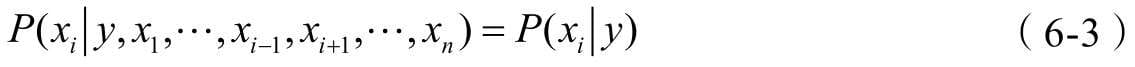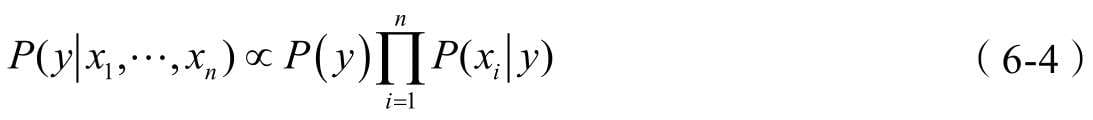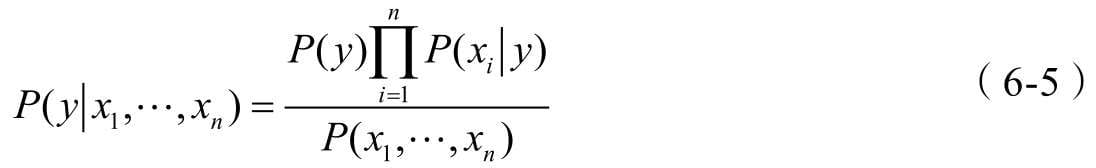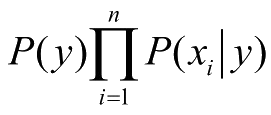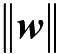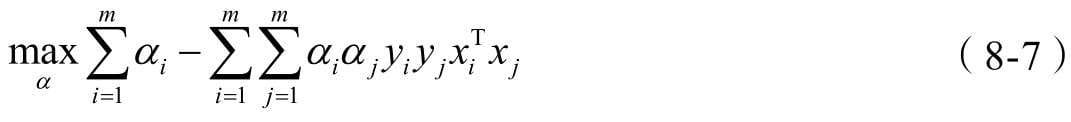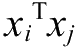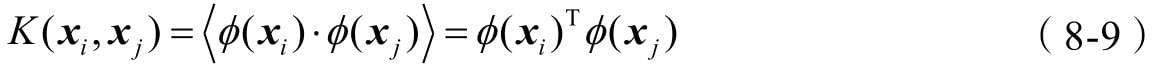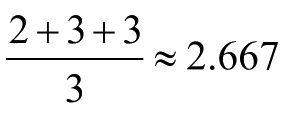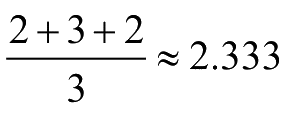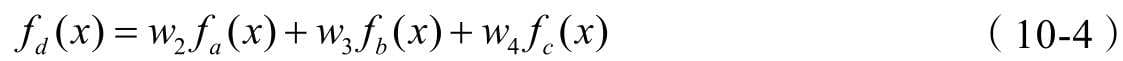书名:机器学习算法的数学解析与Python实现
作者:莫凡
出版社:机械工业出版社
出版时间:2020-01
ISBN:9787111642602
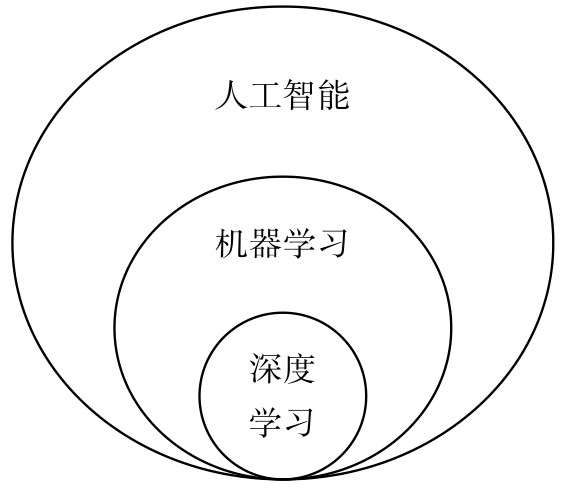
第1章首先介绍机器学习究竟是什么,特别是与“人工智能”“深度学习”这些经常在一起出现的术语究竟有什么关系,又有什么区别。本章也将对机器学习知识体系里的一些常用术语进行简要说明,如果读者此前并不了解机器学习,则可以通过本章了解相关背景知识。
第2章对当前机器学习算法常用的Python编程语言以及相关的Python库进行介绍,同时列举一些常用的功能。
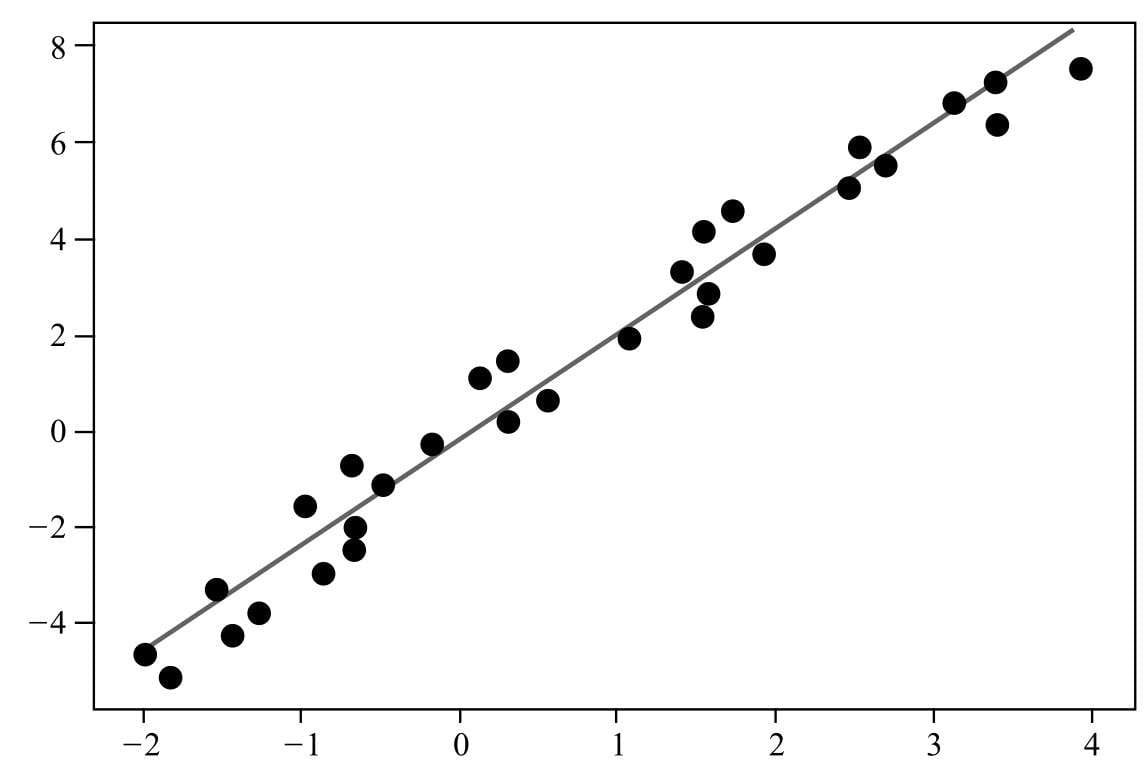
第3章开始正式介绍机器学习算法,要介绍的第一款机器学习算法是线性回归,本章将对回归问题、线性模型和如何用线性模型解决回归问题,以及对机器学习解决问题的主要模式进行介绍。
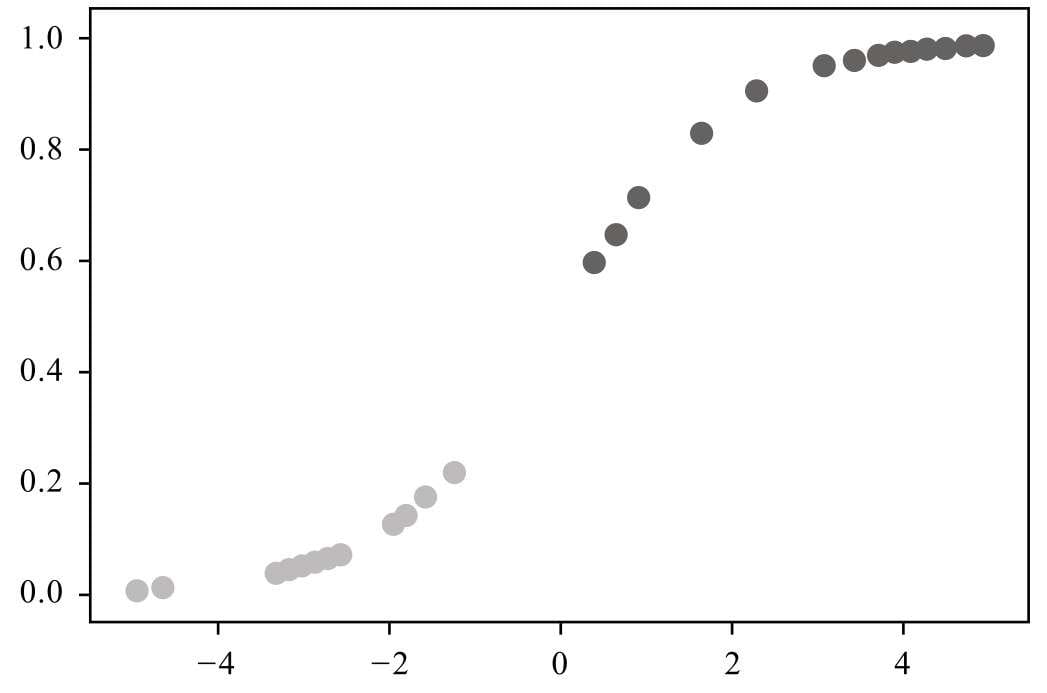
从第4章开始,介绍当下机器学习应用最广的分类问题,第一款解决分类问题的算法是Logistic回归分类算法,即用线性模型结合Logistic函数解决分类问题。
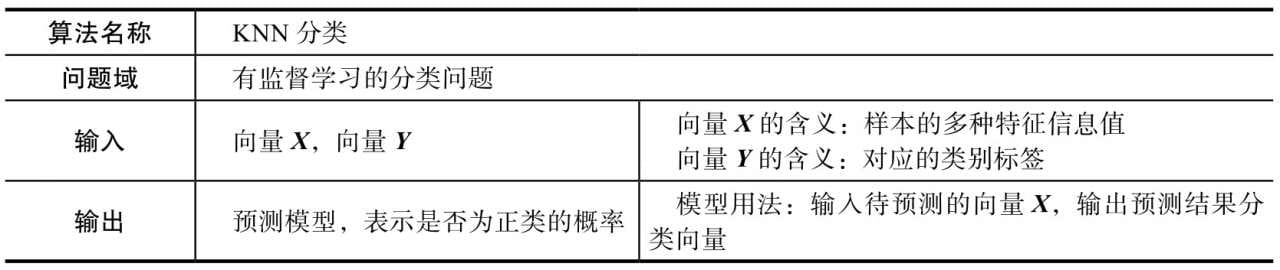
第5章介绍KNN分类算法,这款算法不依赖太复杂的数学原理,因此一般被认为是最直观好懂的分类算法之一。
第6章介绍朴素贝叶斯分类算法,它基于贝叶斯公式设计,理论清晰、逻辑易懂,是一款典型的基于概率统计理论解决分类问题的机器学习算法。
第7章介绍决策树分类算法,这是一款很重要的算法,从思想到结构都对程序员非常友好,当前XGBoost等主流机器学习算法就是在决策树算法的基础上,结合集成学习方法设计而成的。
第8章介绍支持向量机分类算法,这是一款在学术界和工业界都有口皆碑的机器学习模型。在深度学习出现之前,支持向量机被视作最被看好的机器学习算法,能力强、理论美,也是本书中最为复杂的机器模型。
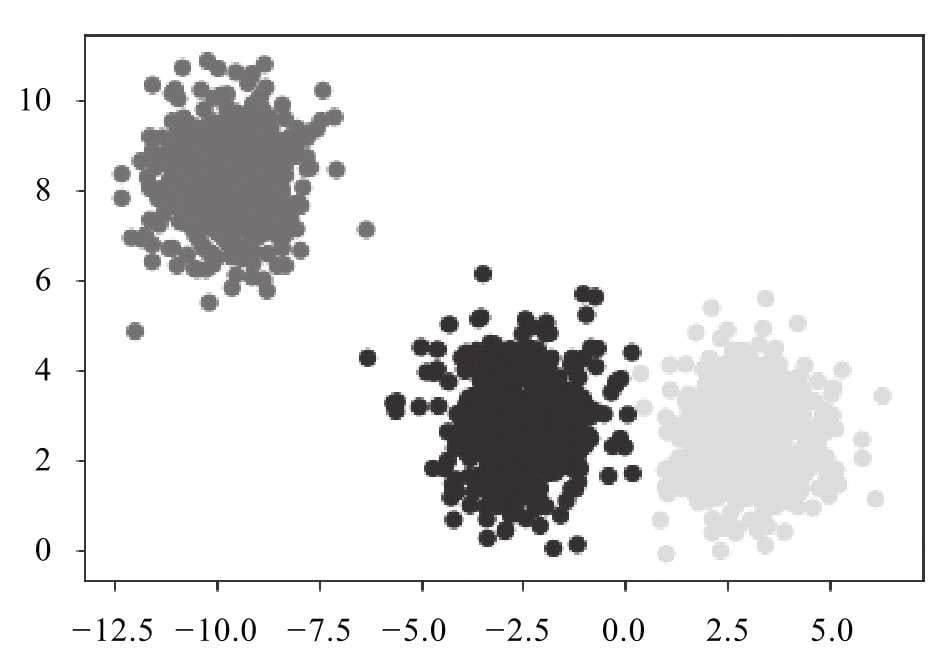
第9章介绍无监督学习的聚类问题,以及简单好懂的聚类算法——K-means聚类算法。
第10章介绍神经网络分类算法,当前大热的深度学习就是从神经网络算法这一支发展而来的,而且大量继承了神经网络的思想和结构,可以作为了解深度学习的预备。
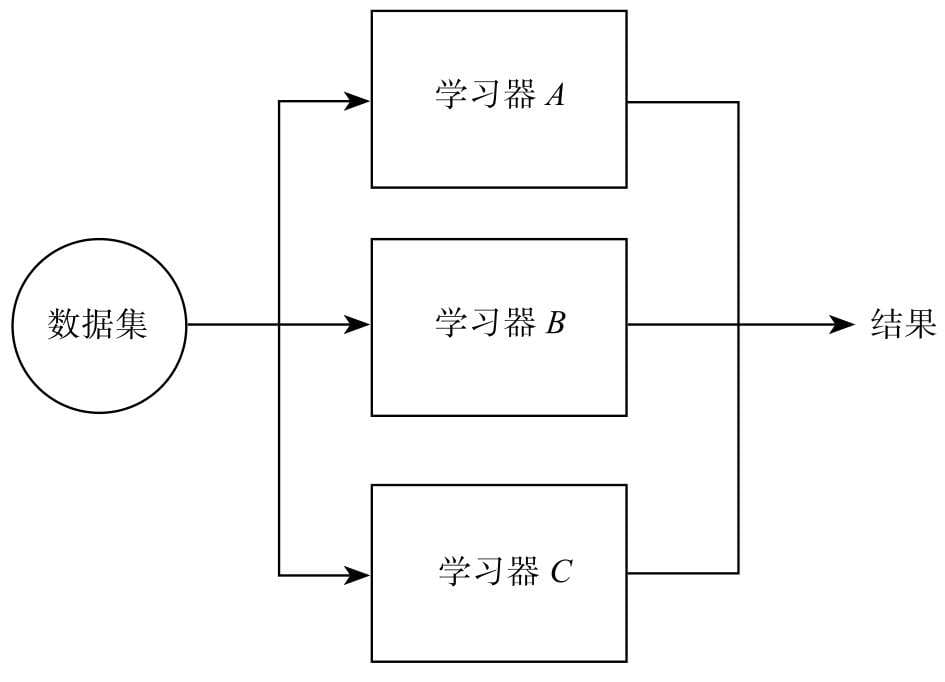
第11章介绍集成学习方法,以及如何通过组合两个以上的机器学习模型来提升预测效果。
第1章 机器学习概述
机器学习知识的三个需求层次
- 设计需求层次
- 思想原理
- 调用需求层次
- 运行流程
- 数学需求层次
- 数学解析
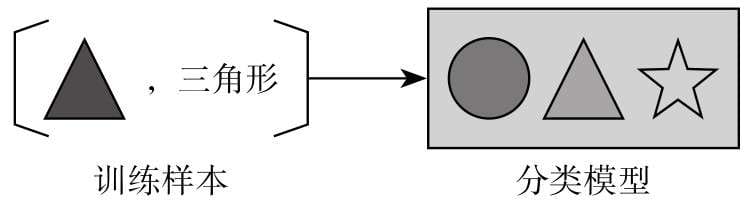
“训练模型”
“训练” == “拟合”
算法
- 数据结构算法
- 算
- 机器学习算法
- 猜
- 我猜是什么
- 我猜中没有
- 猜
“猜数字”游戏
裁判选定一个数字,接着参赛选手也报一个数字,裁判回答他猜大了或猜小了,不断重复这个过程,直到最后猜中。
| 猜数字 | 机器学习 |
|---|---|
| 参赛选手 | 算法模型 |
| 裁判回答 | 损失函数 |
拟合
- 欠拟合
- 准确性不够
- 过拟合
- 泛化性不好
机器学习的基本概念
术语
模型
模型(Model)是机器学习的核心概念。如果认为编程有两大组成部分,即算法和数据结构,那么机器学习的两大组成部分就是模型和数据集。如果之前没有接触过相关概念,想必你现在很希望直观地理解什么是模型,但对模型给出一个简洁又严谨的定义并不容易,你可以认为它是某种机器学习算法在设定参数后的产物,它的作用和编程时用到的函数一样,可以根据某些输入得到某些输出。既然叫机器学习算法,不妨将它想象成一台机器,其上有很多旋钮,这些旋钮就是参数。机器本身是有输入和输出功能的,根据不同的旋钮组合,同一种输入可以产生不同的输出,而机器学习的过程就是找到合适的那组旋钮组合,通过输入得到你所希望的输出。数据集
如果说机器学习的“机器”指的是模型,那么数据集就可以说是驱动着这台机器去“学习”的“燃料”。有些文献将数据集又分为训练集和测试集,其实它们的内容和形式并无差异,只是用在不同的地方:在训练模型阶段使用,就叫作训练集;在测试模型阶段使用,就叫作测试集。数据
我们刚才提到了数据集,数据集就是数据的集合。在机器学习中,我们称一条数据为一个样本(Sample),形式类似一维数组。样本通常包含多个特征(Feature),如果是用于分类问题的数据集,还会包含类别(Class Label)信息,如果是回归问题的数据集,则会包含一个连续型的数值。特征
这个术语又容易让你产生误解了。我们一般把可以作为人或事物特点的征象、标志等称作特征,譬如这个人鼻子很大,这就是特征,但在机器学习中,特征是某个对象的几个记录维度。我们都填写过个人信息表,特征就是这张表里的空格,如名字、性别、出生日期、籍贯等,一份个人信息表格可以看成一个样本,名字、籍贯这些信息就称作特征。前面说数据形式类似一维数组,那么特征就是数组的值。向量
向量为线性代数术语,机器学习模型算法的运算均基于线性代数法则,不妨认为向量就是该类算法所对应的“数据结构”。一条样本数据就是以一个向量的形式输入模型的。一条监督学习数据的向量形式如下:[特征X1值,特征X2值,…, Y1值]
矩阵
矩阵为线性代数术语,可以将矩阵看成由向量组成的数组,形式上也非常接近二维数组。前面所说的数据集,通常就是以矩阵的形式输入模型的,常见的矩阵形式如下:[[特征X1值,特征X2值,…, Y1值],
'[特征X1值,特征X2值,…, Y2值],
…
[特征X1值,特征X2值,…, Yn值]]
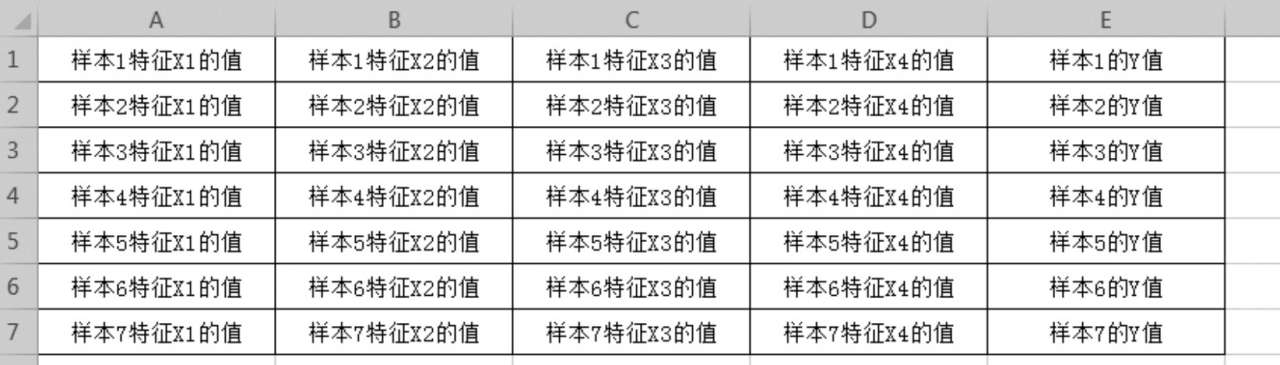
其实这个组织形式非常类似电子表格,不妨就以电子表格来对照理解。每一行就是一个样本,每一列就是一个特征维度,譬如某个数据集一共包括了7个样本,那就是有7行数据,每个样本又都有4个维度的特征,那就是每行数据有4列,用电子表格表示如图1-2所示,其中,A~D列为特征,E列为结果。
常用函数
- 假设函数(Hypothesis Function)
\[ H(x) \]
这里的 \(x\) 可以简单理解成矩阵形式的数据,我们把数据“喂”给假设函数,假设函数就会返回一个结果,而这个结果正是机器学习所得到的预测结果。
- 损失函数(Loss Function)/ 目标函数
\[ L(x) \]
\(L\) 代表 Loss,这里的 \(x\) 是假设函数的预测结果。
函数返回值越大,表示结果偏差越大。
- 成本函数(Cost Function)
\[ J(x) \]
这里的 \(x\) 也是假设函数的预测结果。
函数返回值越大,表示偏差越大。
| 差别 | 损失函数 | 成本函数 |
|---|---|---|
| 对象 | 单个样本 | 整个数据集 |
| 角度 | 微观 | 宏观 |
成本函数是由损失函数计算得到的。
\(J(x) = Sum(L(x))\)
或者
\(J(x) = Avg(L(x))\)
机器学习的基本模式
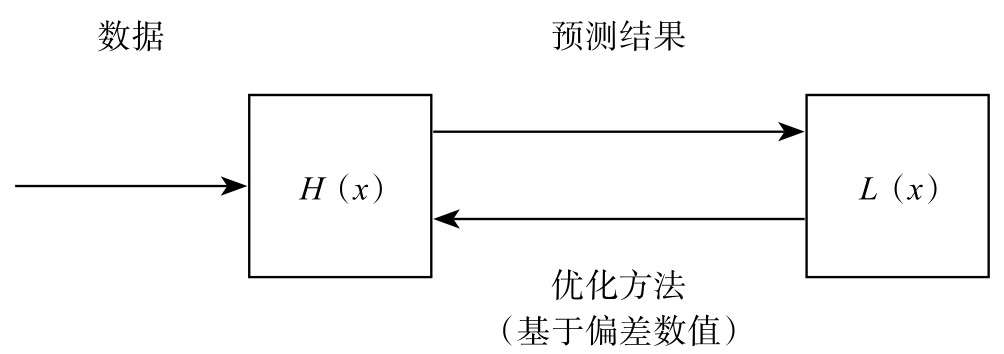
- 数据
- 假设函数
- 损失函数
优化方法
\[ min(L(x)) \]
\[ 新参数值 = 旧参数值 - 损失值 \]
牛顿法、拟牛顿法、共轭梯度法
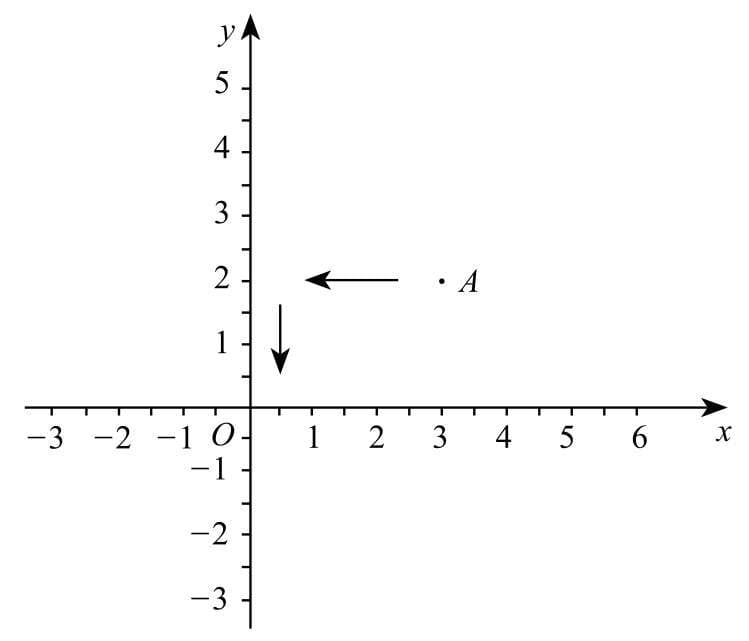
梯度下降(Gradient Descent)法是机器学习中常用的一种优化方法
梯度下降(Gradient Descent)法是机器学习中常用的一种优化方法,梯度是微积分学的术语,某个函数在某点的梯度指向该函数取得最大值的方向,那么它的反方向自然就是取得最小值的方向。所以只要对损失函数采用梯度下降法,让假设函数朝着梯度的负方向更新权值,就能达到令损失值最小化的效果。
倒车:
1. 方向
1. 大小
- 批量梯度下降(Batch Gradient Descent
- 每次迭代都使用全部样本
- 随机梯度下降(Stochastic Gradient Descent
- 每次迭代只使用一个样本
因为需要计算的样本小,随机梯度下降的迭代速度更快,但更容易陷入局部最优,而不能达到全局最优点。
机器学习问题分类
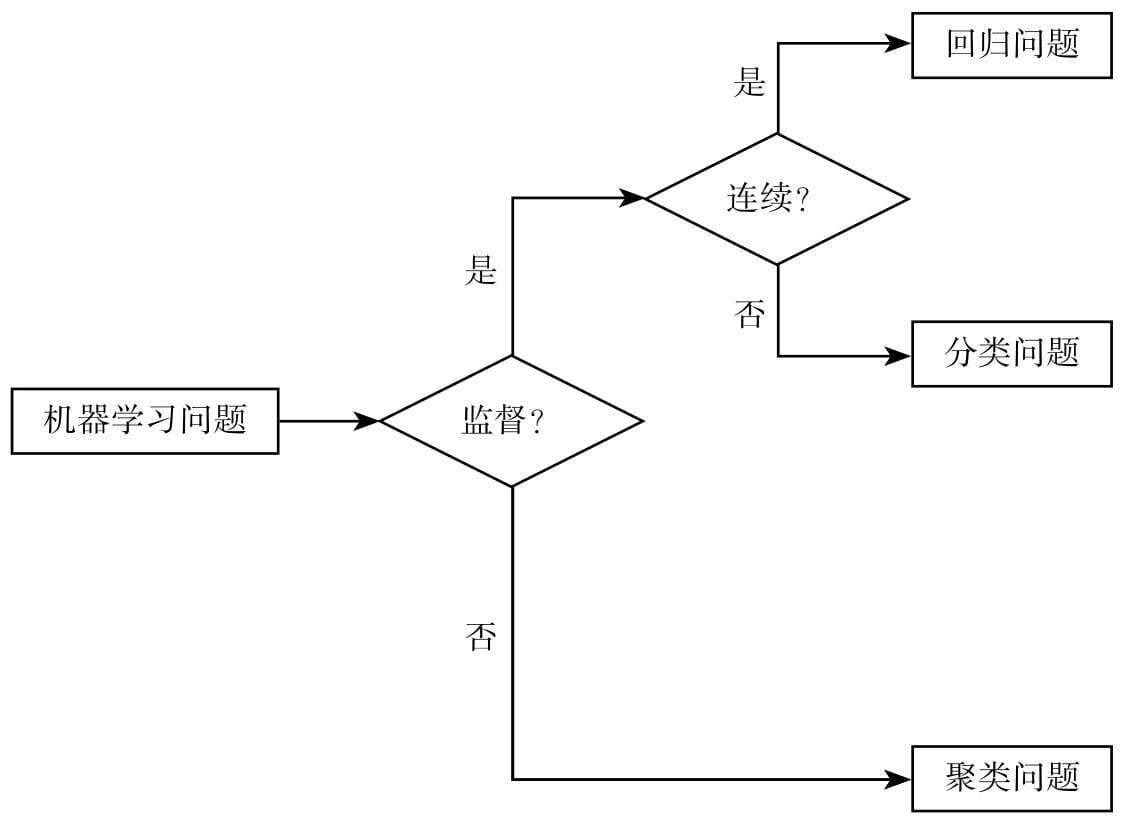
无监督学习(Unsupervised Learning)
有监督学习(Supervised Learning)
常用的机器学习算法
- 线性回归算法
- 这是最基本的机器学习算法,但麻雀虽小,五脏俱全,该算法称得上是机器学习算法界的“Hello World”程序,是用线性方法解决回归问题。
- Logistic回归分类算法
- 这可谓是线性回归算法的“孪生兄弟”,其核心思想仍然是线性方法,但套了一件名为Logistic函数的“马甲”,使得其具有解决分类问题的能力。
- KNN分类算法
- 该算法是本书介绍的分类算法中唯一一个不依赖数学或统计模型,纯粹依靠“生活经验”的算法,它通过“找最近邻”的思想解决分类问题,其核心思想和区块链技术中的共识机制有着深远的关系。
- 朴素贝叶斯分类算法
- 这是一套能够刷新你世界观的算法,它认为结果不是确定性的而是概率性的,你眼前所见的不过是概率最大的结果罢了。当然,算法是用来解决问题的,朴素贝叶斯分类算法解决的是分类问题。
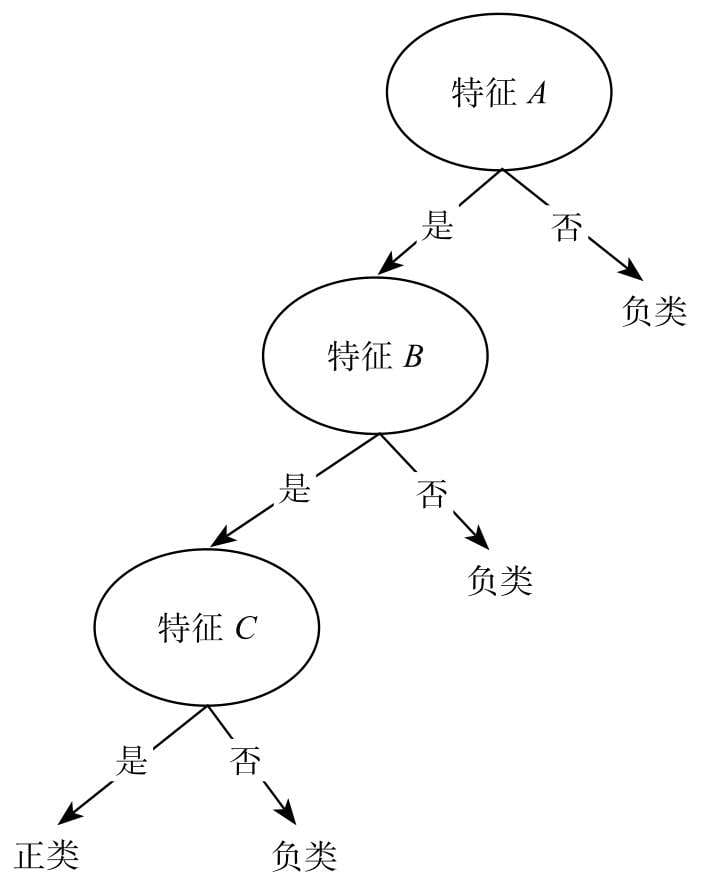
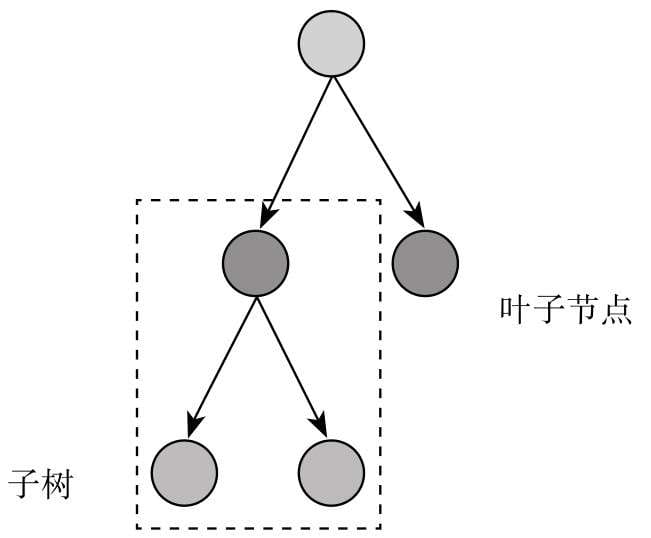
- 决策树分类算法
- 如果程序员的思维逻辑能够用if-else来概括的话,决策树分类算法应该就是最接近程序员逻辑的机器学习算法。
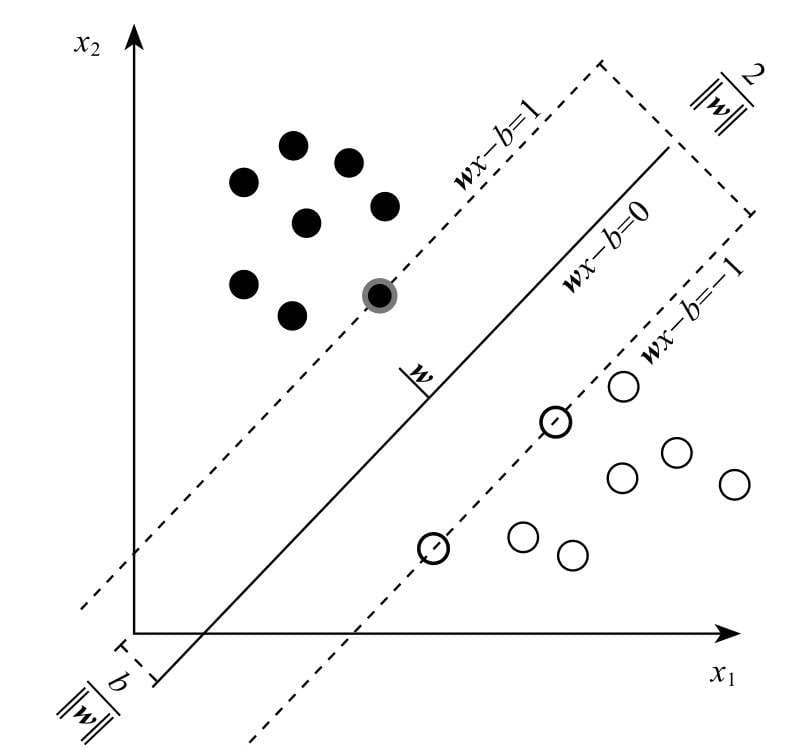
- 支持向量机分类算法
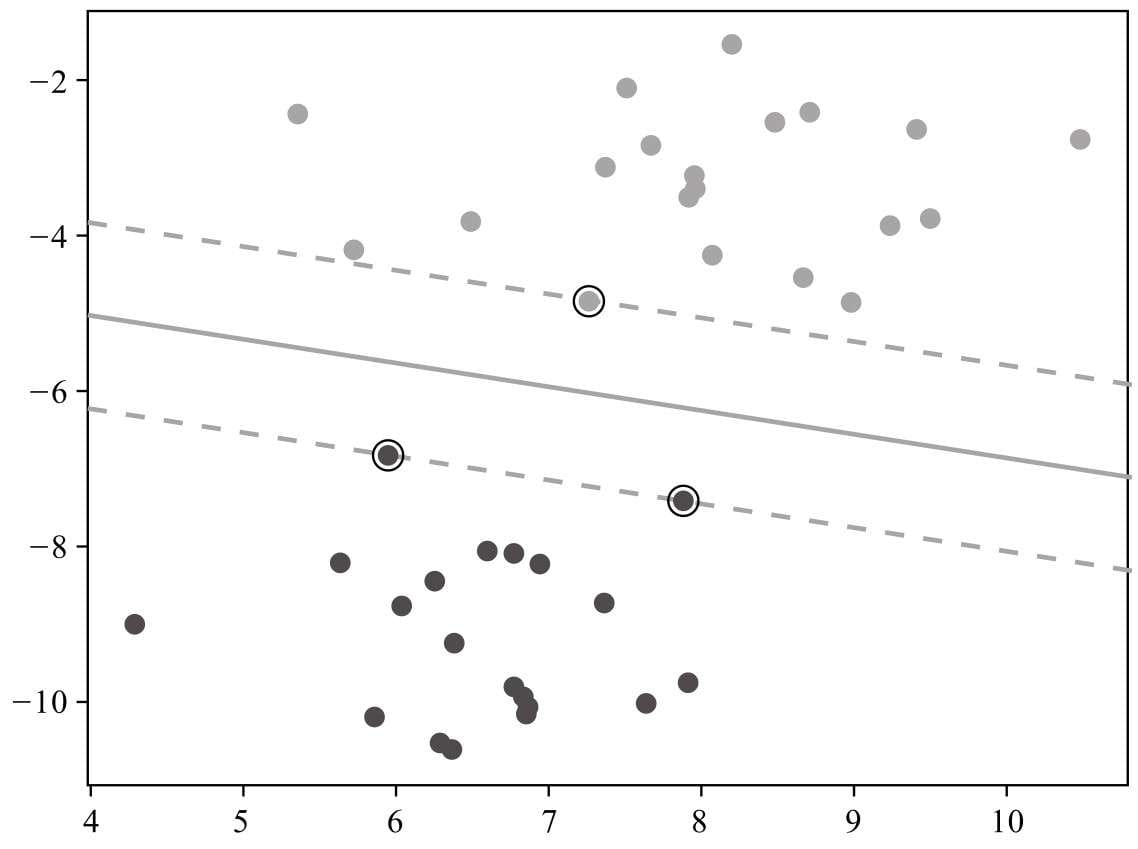
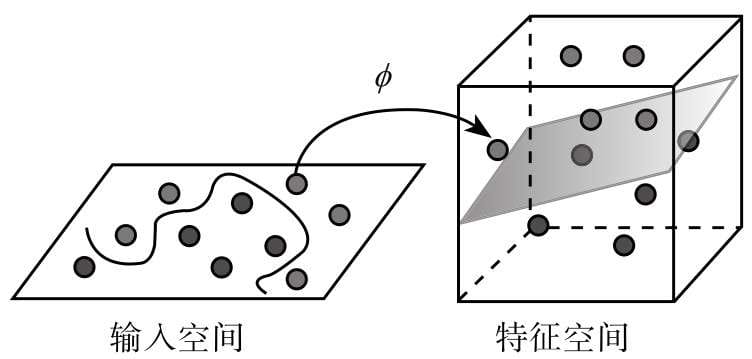
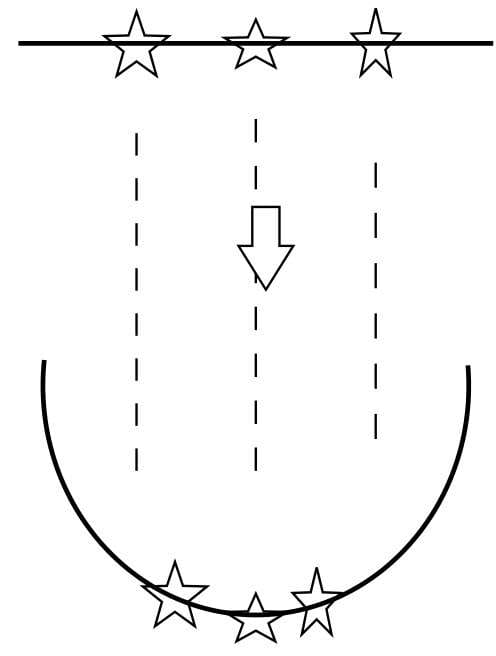
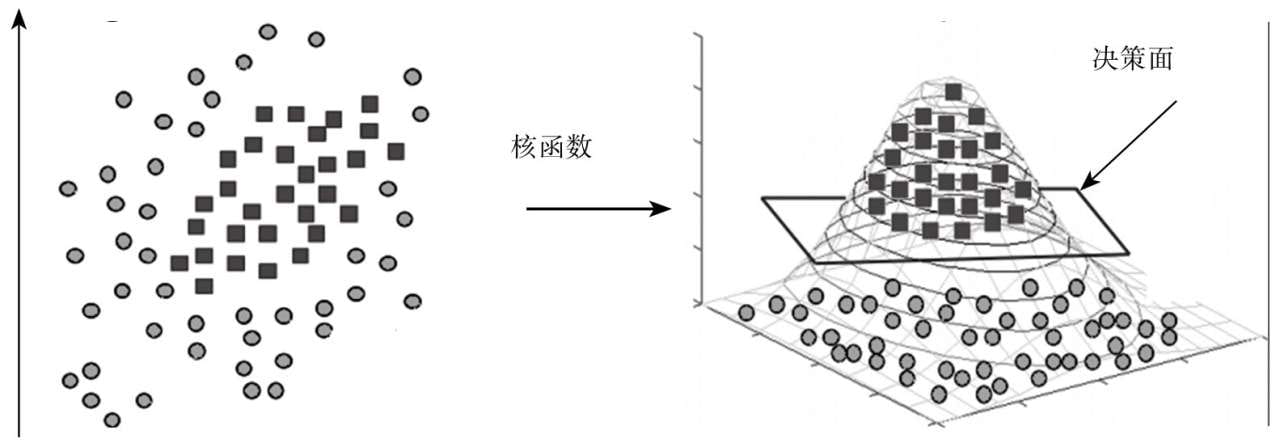
- 如果说Logistic回归分类算法是最基本的线性分类算法,那么支持向量机则是线性分类算法的最高形式,同时也是最“数学”的一种机器学习算法。该算法使用一系列令人拍案叫绝的数学技巧,将线性不可分的数据点映射成线性可分,再用最简单的线性方法来解决问题。
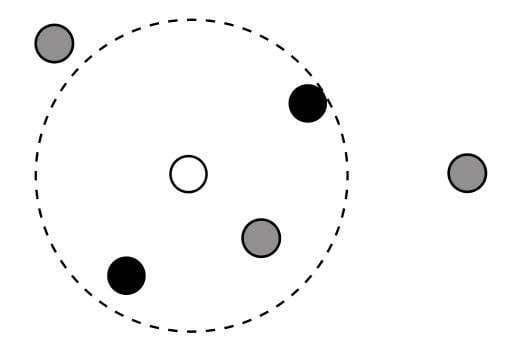
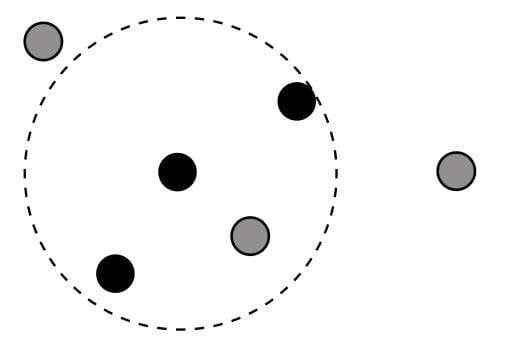
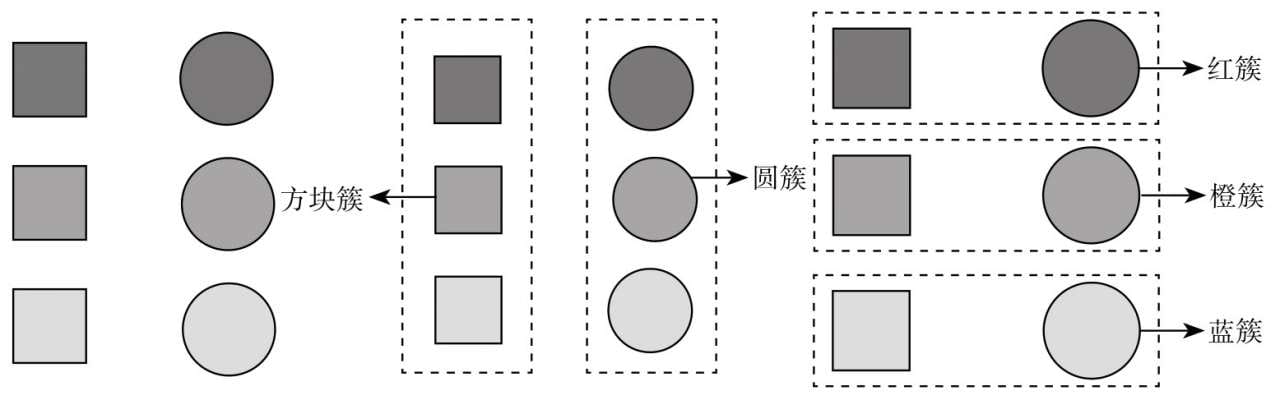
- K-means聚类算法
- 有监督学习是当前机器学习的一种主流方式,但样本标记需要耗费大量人工成本,容易出现样本累积规模庞大,但标记不足的问题。无监督学习则是一种无须依赖标记样本的机器学习算法,聚类算法就是其中具有代表性的一种,而K-means是聚类算法中的典型代表。
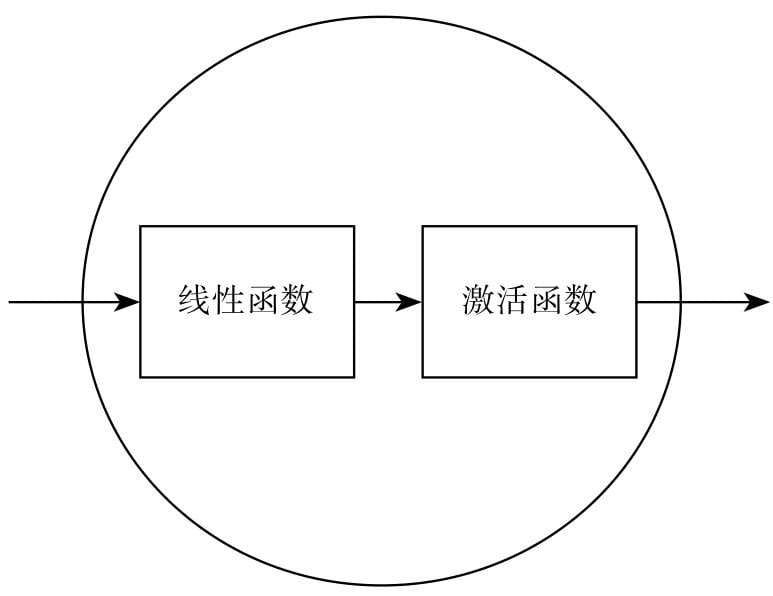
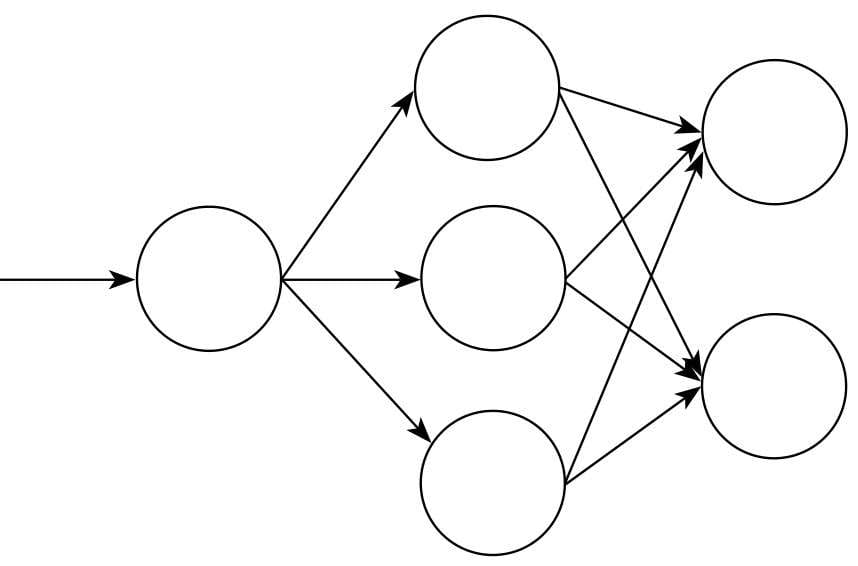
- 神经网络分类算法
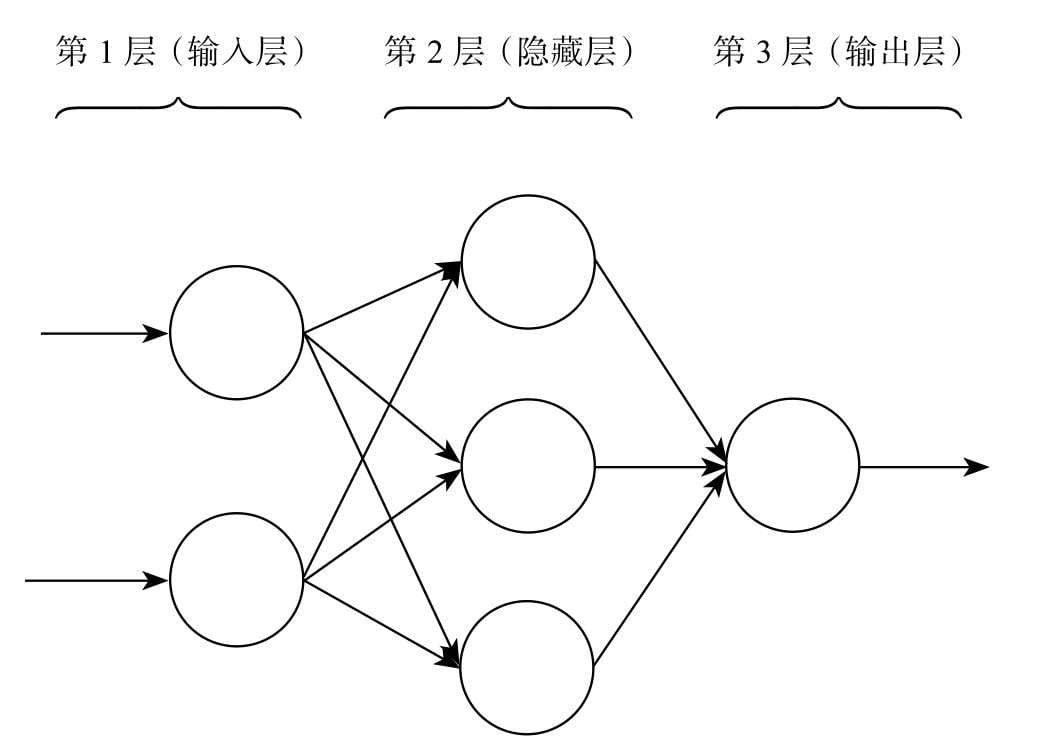
- 神经网络就是由许多神经元连接所构成的网络,很多人认为该算法是一种仿生算法,模仿的对象正是我们的大脑。神经网络分类算法也是当下热门的深度学习算法的起点。
机器学习算法的性能衡量指标
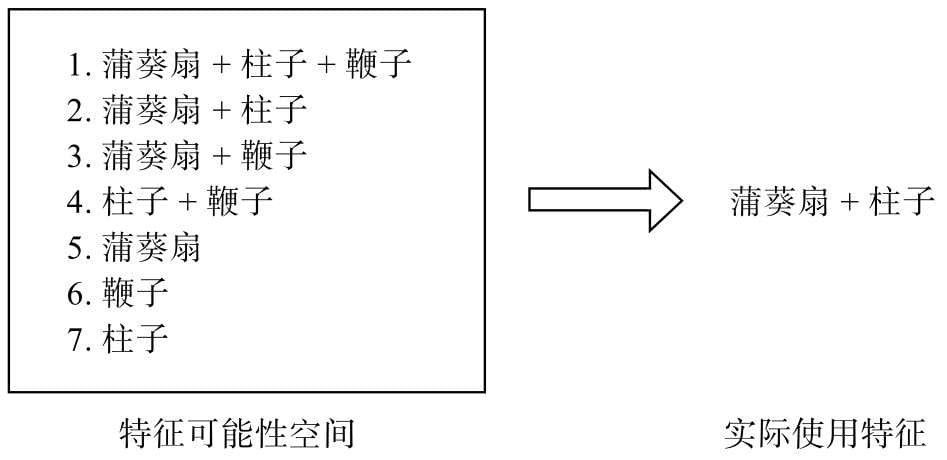
NFL定律(No Free Lunch Theorem,中文一般翻译为“没有免费午餐定律”)。
- TP:True Positive,预测结果为正类,且与事实相符,即事实为正类。
- TN:True Negative,预测结果为负类,且与事实相符,即事实为负类。
- FP:False Positive,预测结果为正类,但与事实不符,即事实为负类。
- FN:False Negative,预测结果为负类,但与事实不符,即事实为正类。
常用的指标
- 准确率(Accuracy)

- 精确率(Precision),又叫查准率

- 召回率(Recall),又叫查全率

数据对算法结果的影响
数据决定了算法的能力上限
数据决定了模型能够达到的上限,而算法只是逼近这个上限。
特征工程
机器学习模型正是从这些特征中进行学习,特征有多少价值,机器才能学多少价值。
第2章 机器学习所需的环境
Python 简介
安装
1 | # pip |
使用
1 | # library.a_class |
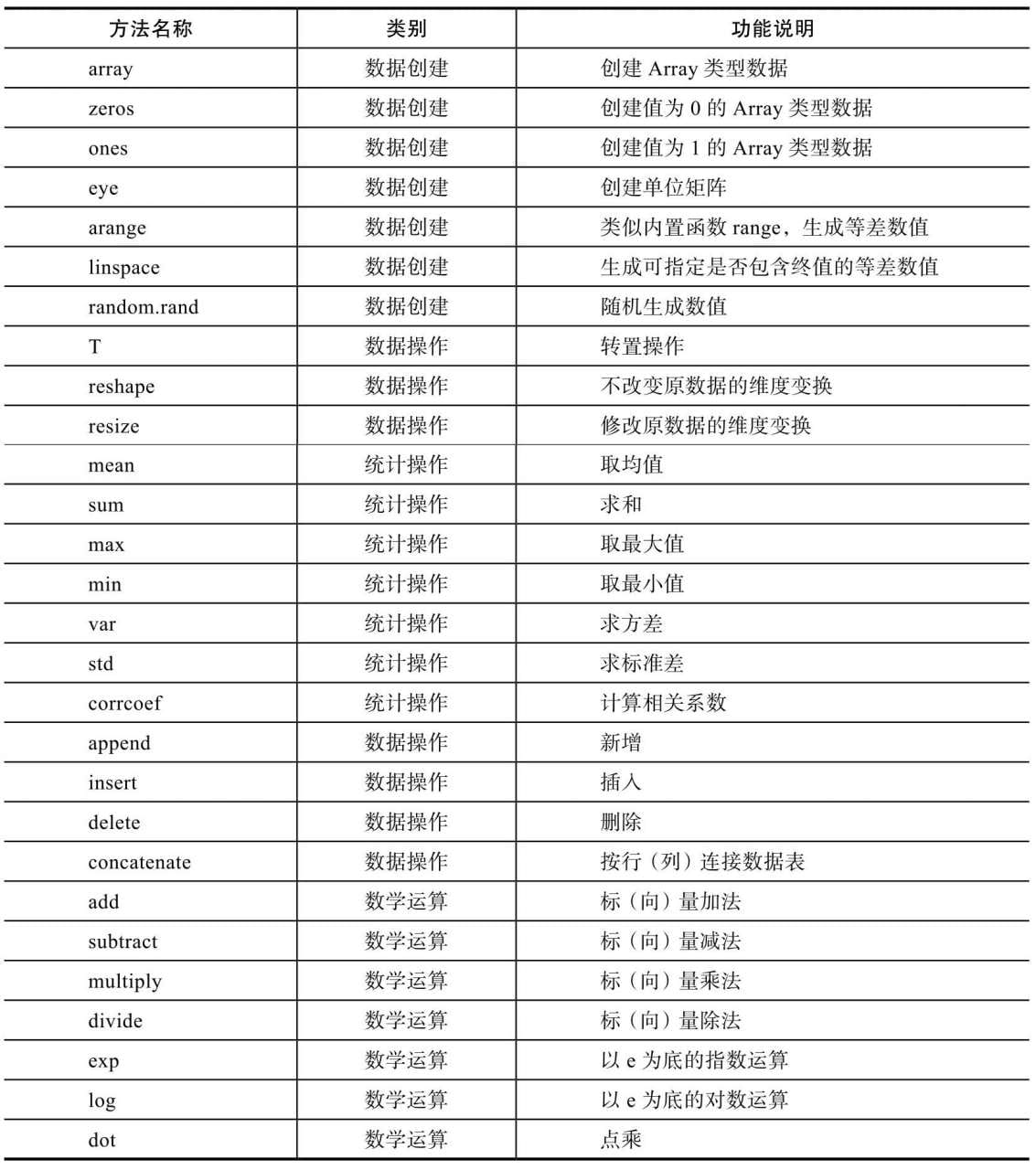
Numpy 简介
Numpy是Python语言的科学计算支持库,提供了线性代数、傅里叶变换等非常有用的数学工具。Numpy是Python圈子里非常知名的基础库,即使你并不直接进行科学计算,但如图像处理等相关功能库,其底层实现仍需要数学工具进行支持,则需要首先安装Numpy库。
安装
1 | pip install -U numpy |
使用
1 | import numpy as np |
Scikit-Learn 简介
正如机器学习中推荐使用Python语言,用Python语言使用机器学习算法时,推荐使用Scikit-Learn工具,或者应该反过来,现在机器学习推荐使用Python,正是因为Python拥有Scikit-Learn这样功能强大的支持包,它已经把底层的脏活、累活都默默完成了,让使用者能够将宝贵的注意力和精力集中在解决问题上,极大地提高了产出效率。

安装
1 | # pip |
使用
1 | import sklearn |
调用机器学习算法也非常简单,Scikit-Learn库已经将算法按模型分类,查找起来非常方便。如线性回归算法可以从线性模型中找到,用法如下:
1 | from sklearn import linear_model |
Logistic回归算法也是依据线性模型
1 | from sklearn.linear_model import LogisticRegression |
类似的还有基于近邻模型的KNN算法
1 | from sklearn.neighbors import NearestNeighbors |
生成模型后,一般使用fit方法给模型“喂”数据及进行训练。完成训练的模型可以使用predict方法进行预测。
Scikit-Learn库对机器学习算法进行了高度封装,使用过程非常简单,只要根据格式填入数据即可,不涉及额外的数学运算操作,甚至可以说只要知道机器学习算法的名字和优劣,就能直接使用,非常便利。
Pandas简介
Pandas是Python语言中知名的数据处理库。数据是模型算法的燃料,也决定了算法能够达到的上限。一般在学习中接触的数据都十分规整,可以直接供模型使用。但实际上,从生产环境中采集得到的“野生”数据则需要首先进行数据清洗工作,最常见的如填充丢失字段值。数据清洗工作一般使用Pandas来完成,前文所提到的特征工程也可通过Pandas完成。
安装
1 | # pip |
Pandas的基本用法
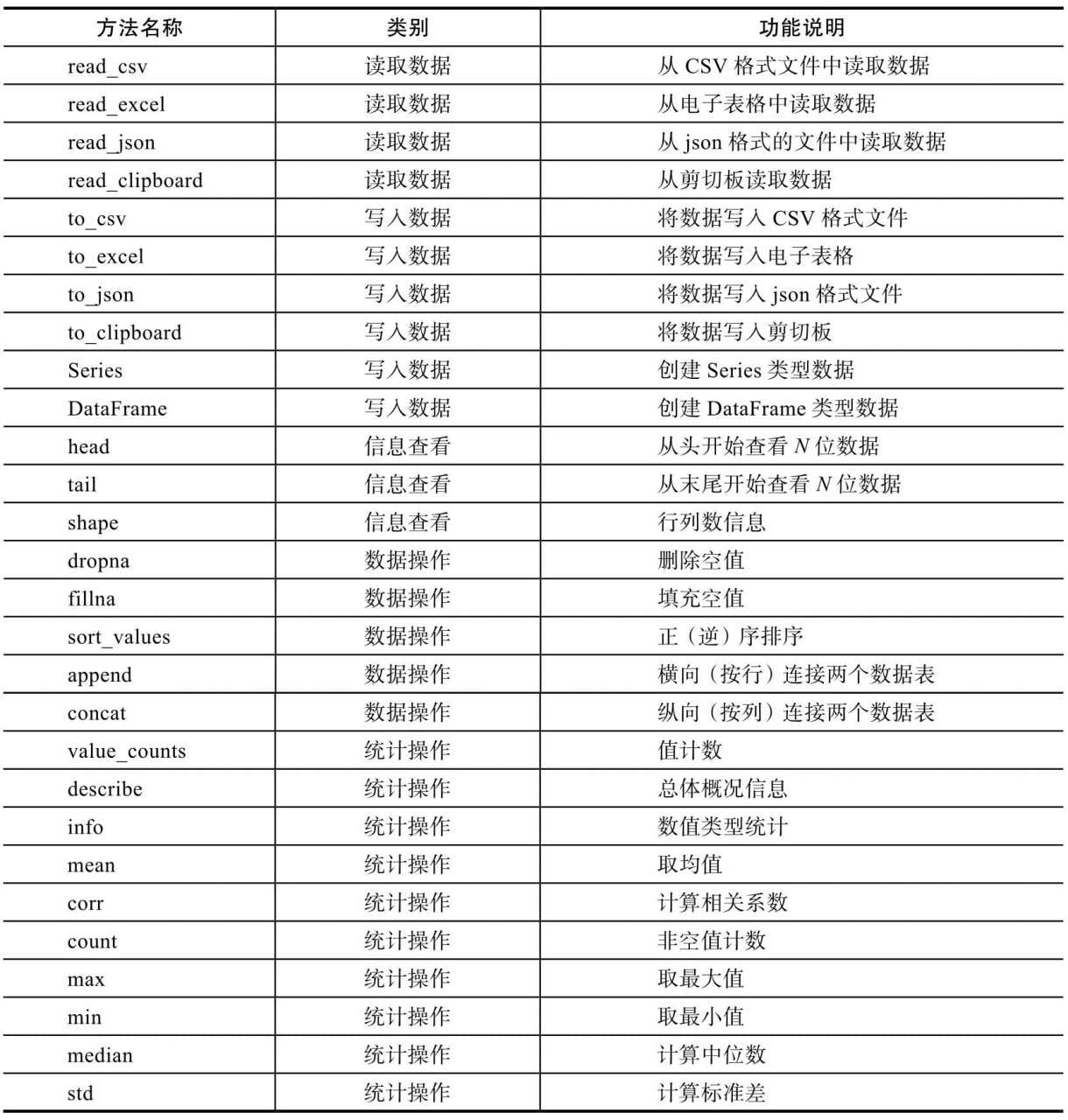
Pandas针对数据处理的常用功能而设计,具有从不同格式的文件中读写数据的功能,使用Pandas进行一些统计操作特别便利。与Numpy类似,Pandas也有两个核心的数据类型,即Series和DataFrame。
- Series:一维数据,可以认为是一个统计功能增强版的List类型。
- DataFrame:多维数据,由多个Series组成,不妨认为是电子表格里的Sheet。使用Pandas包很简单,只要import导入即可。业界习惯在导入时使用“pd”作为它的别名:
1 | import pandas as pd |
第3章 线性回归算法
机器学习涉及的知识面很广,但总的来说有两条主线,
- 问题
- 模型