Paper: Training Linear SVMs in Linear Time
回到这篇时间检验奖的论文,它解决的是大规模优化支持向量机的问题,特别是线性支持向量机。
这篇文章第一次提出了简单易行的线性支持向量机实现,包括对有序回归(Ordinal Regression)的支持。
算法对于分类问题达到了 O(sn)(其中 s 是非 0 的特征数目而 n 是数据点的个数),也就是实现了线性复杂度,而对有序回归的问题达到了 O(snlog(n)) 的复杂度。
算法本身简单、高效、易于实现,并且理论上可以扩展到核函数(Kernel)的情况。
在此之前,很多线性支持向量机的实现都无法达到线性复杂度 。
比如当时的 LibSVM(台湾国立大学的学者发明)、SVM-Torch、以及早期的 SVM-Light 中采用的分解算法(Decomposition Method)都只能比较有效地处理大规模的特征。
而对于大规模的数据 (n),则是超线性(Super-Linear)的复杂度。
另外的一些方法,能够训练复杂度线性地随着训练数据的增长而增长,但是却对于特征数 N 呈现了二次方 (N^2) 的复杂度。
因此之前的这些方法无法应用到大规模的数据上。
这样的情况对于有序回归支持向量机更加麻烦。
从德国学者拉尔夫·赫布里希(Ralf Herbrich)提出有序回归支持向量机以来,一直需要通过转化为普通的支持向量机的分类问题而求解。
这个转换过程需要产生 O(n^2) 的训练数据,使得整个问题的求解也在这个量级的复杂度。
这篇文章里,Thorsten 首先做的是对普通的支持向量机算法的模型形式(Formalism)进行了变形。
他把传统的分类支持向量机(Classification SVM)写成了结构化分类支持向量机(Structural Classification SVM),并且提供了一个定理来证明两者之间的等价性。
粗一看,这个等价的结构化分类支持向量机并没有提供更多有价值的信息。
然而这个新的优化目标函数的对偶(Dual)形式,由于它特殊的稀疏性,使它能够被用来进行大规模训练。
紧接着,Thorsten 又把传统的有序回归支持向量机的优化函数,写成了结构化支持向量机的形式,并且证明了两者的等价性。
把两种模型表达成结构化向量机的特例之后,Thorsten 开始把解决结构化向量机的一种算法——切割平面算法(Cutting-Plane),以下称 CP 算法,运用到了这两种特例上。
首先,他展示了 CP 算法在分类问题上的应用。
简单说来,这个算法就是保持一个工作集合(Working Set),来存放当前循环时依然被违反的约束条件(Constraints),然后在下一轮中集中优化这部分工作集合的约束条件。
整个流程开始于一个空的工作集合,每一轮优化的是一个基于当前工作集合的支持向量机子问题,算法直到所有的约束条件的误差小于一个全局的参数误差为止。
Thorsten 在文章中详细证明了这个算法的有效性和时间复杂度。
相同的方法也使得有序回归支持向量机的算法能够转换成为更加计算有效的优化过程。
Thorsten 在文章中做了详尽的实验来展现新算法的有效性。
从数据的角度,他使用了 5 个不同的数据集,分别是路透社 RCV1 数据集的好几个子集。
数据的大小从 6 万多数据点到 80 多万数据点不等,特征数也从几十到四万多特征不等,这几种不同的数据集还是比较有代表性的。
从方法的比较上来说,Thorsten 主要比较了传统的分解方法。
有两个方面是重点比较的,第一就是训练时间。
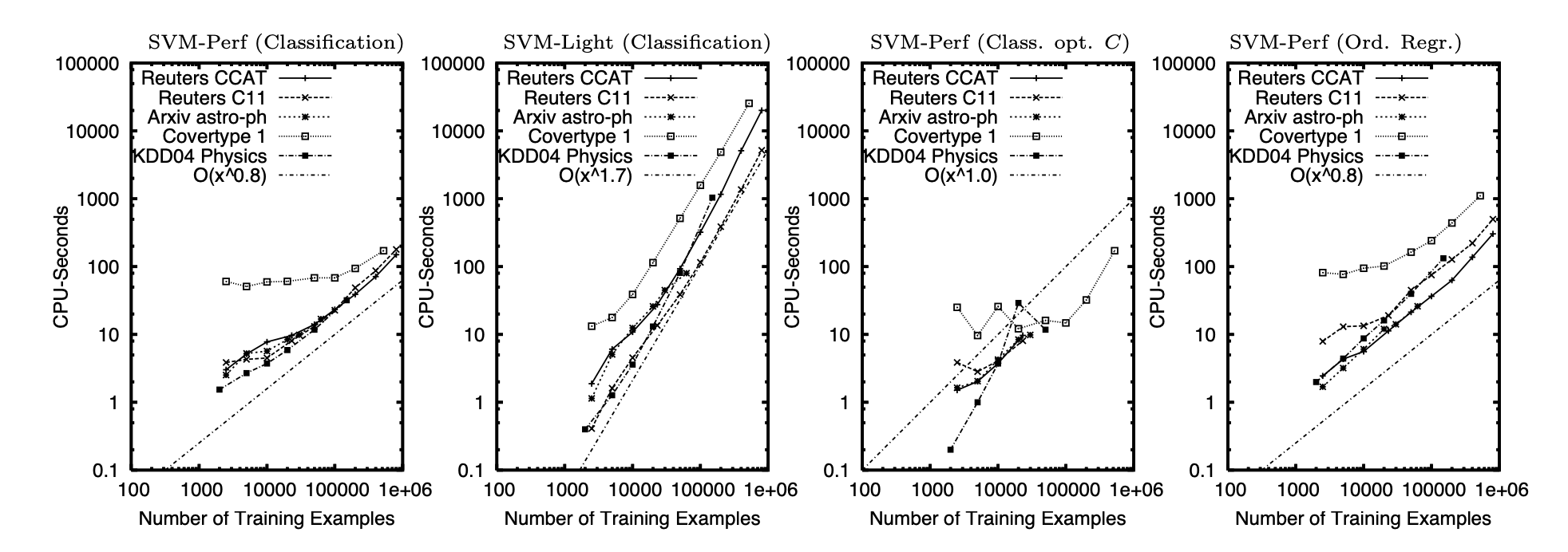
在所有的数据集上,这篇文章提出的算法都比传统算法快几个数量级,提速达到近 100 倍。
而有序回归的例子中,传统算法在所有数据集上都无法得到最后结果。
Thorsten 进一步展示了训练时间和数据集大小的线性关系,从而验证了提出算法在真实数据上的表现。
第二个重要的比较指标是算法的准确度是否有所牺牲。
因为有时候算法的提速是在牺牲算法精度的基础上做到的,因此验证算法的准确度就很有意义。
在这篇文章里,Thorsten 展示,提出的算法精度,也就是分类准确度并没有统计意义上的区分度,也让这个算法的有效性有了保证。
Thorsten 在他的软件包 SVM-Perf 中实现了这个算法。
这个软件包一度成了支持向量机研究和开发的标准工具。