笑话: 频率学派 & 贝叶斯学派
有个病人找医生看病,医生检查之后对他说:“你这病说得上是九死一生,但多亏到我这里来看了。不瞒你说,在你之前我已经看了九个得一同样病的患者,结果他们都死了,那你这第十个就一定能看得好啦,妥妥的!”
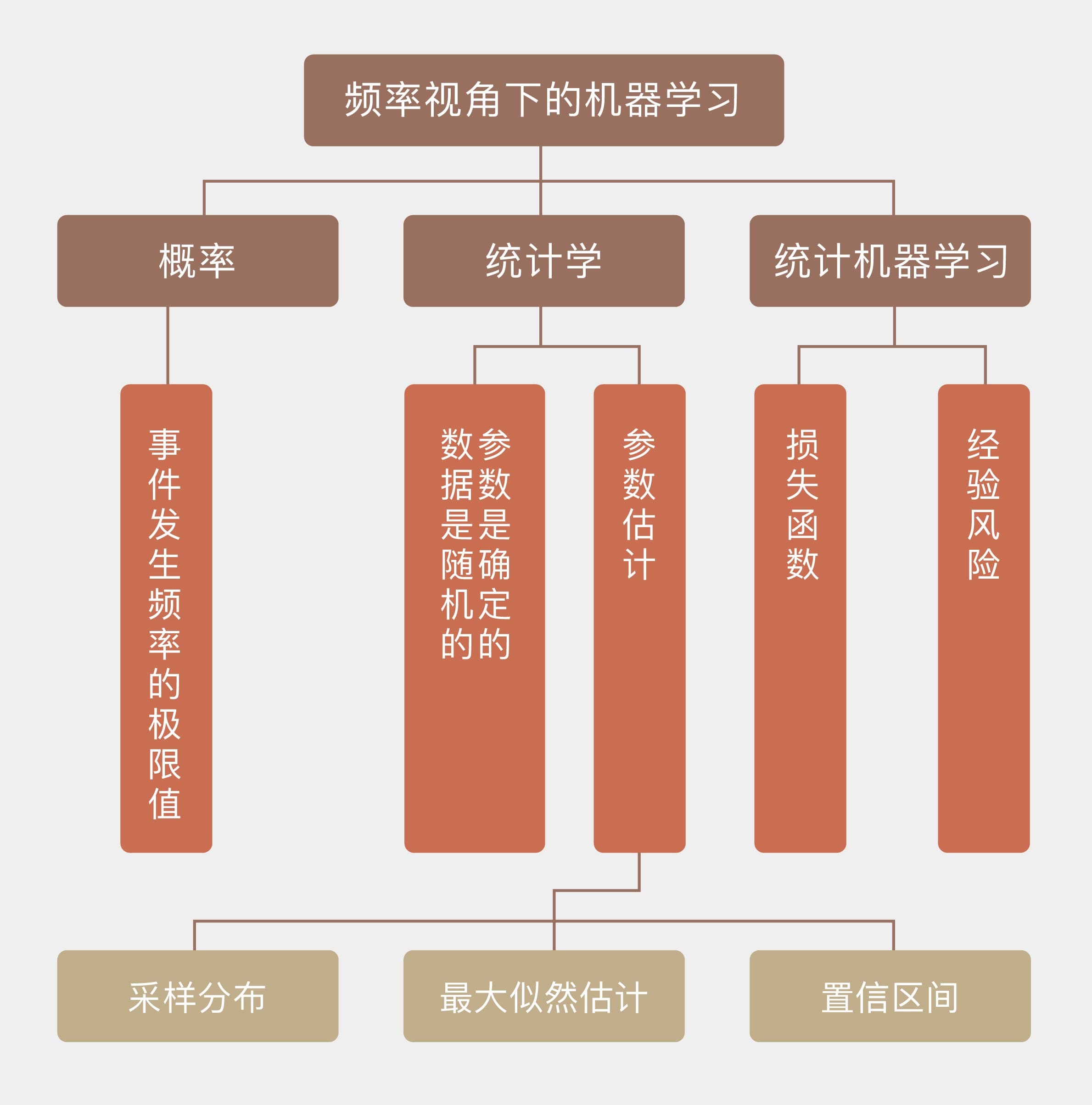
频率学派口中的概率表示的是事件发生频率的极限值,它只有在无限次的独立重复试验之下才有绝对的精确意义。
在频率学派眼中,当重复试验的次数趋近于无穷大时,事件发生的频率会收敛到真实的概率之上。这种观点背后暗含了一个前提,那就是概率是一个确定的值,并不会受单次观察结果的影响。
频率统计理论的核心在于认定待估计的参数是固定不变的常量,讨论参数的概率分布是没有意义的;而用来估计参数的数据是随机的变量,每个数据都是参数支配下一次独立重复试验的结果。由于参数本身是确定的,那频率的波动就并非来源于参数本身的不确定性,而是由有限次观察造成的干扰而导致。
这可以从两个角度来解释:
- 一方面,根据这些不精确的数据就可以对未知参数的精确取值做出有效的推断;
- 另一方面,数据中包含的只是关于参数不完全的信息,所以从样本估计整体就必然会产生误差。
统计学的核⼼任务之一是根据从总体中抽取出的样本,也就是数据来估计未知的总体参数。参数的最优估计可以通过样本数据的分布,也就是 采样分布(sampling distribution) 来求解,由于频率统计将数据看作随机变量,所以计算采样分布是没有问题的。确定采样分布之后,参数估计可以等效成一个最优化的问题,而频率统计最常使用的最优化方法,就是 最大似然估计(maximum likelihood estimation)。
那么如何来度量作为随机变量的估计值和作为客观常量的真实值之间的偏差呢?置信区间(confidence interval) 就是频率学派给出的答案。
频率主义解决统计问题的基本思路如下:
- 参数是确定的,
- 数据是随机的,
- 利用随机的数据推断确定的参数,
- 得到的结果也是随机的。
将频率主义“参数确定,数据随机”的思路应用在机器学习当中,得到的就是统计机器学习(statistical learning)。
和参数相关的信息全部来源于数据,输出的则是未知参数唯一的估计结果,这是统计机器学习的核心特征。
要点
- 频率学派认为概率是随机事件发生频率的极限值;
- 频率学派执行参数估计时,视参数为确定取值,视数据为随机变量;
- 频率学派主要使用最大似然估计法,让数据在给定参数下的似然概率最大化;
- 频率学派对应机器学习中的统计学习,以经验风险最小化作为模型选择的准则。